4.8.1.3. Ảnh hưởng của chiều dài nhịp đến độ vòng của đường dây cáp.
a) Kết quả thí nghiệm
Đề tài đã tiến hành thí nghiệm như sau: Cố định lực căng của đường dây cáp H = 5500N và tải trọng đều q = 0,2 N/cm; thay đổi chiều dài nhịp = 2000- 2800 cm. Kết quả thí nghiệm đo độ vòng được ghi ở bảng 4.5.
Bảng 4.5. Ảnh hưởng của chiều dài nhịp đến độ vòng khi lực căng ngang H = 5500 N và tải trọng đều q = 0.2N/cm
Chiều dài nhịp
| Độ vòng lớn nhất f (cm) | |||||||
Lần 1 | Lần 2 | Lần 3 | Trung bình | Hồi quy thực nghiệm | Lý thuyết | Sai số % | ||
1 | 2000 | 18 | 20 | 19 | 19 | 19.5 | 18.0 | 8 |
2 | 2200 | 21 | 19 | 20 | 20 | 19.1 | 21.0 | 9 |
3 | 2400 | 22 | 21 | 23 | 22 | 21.9 | 25.0 | 12 |
4 | 2600 | 26 | 27 | 28 | 27 | 28.1 | 30.0 | 6 |
5 | 2800 | 39 | 38 | 37 | 38 | 37.5 | 35.0 | 7 |
Có thể bạn quan tâm!
-
Sự Ảnh Hưởng Của Độ Dài Nhịp Cáp Đến Biên Độ Cực Đại Của Dao Động Giỏ Đựng Thanh Long -
Phương Pháp Xác Định Các Đại Lượng Nghiên Cứu Và Thiết Bị Đo -
Bố Trí Thí Nghiệm Đo Lực Căng Ngang Và Độ Vòng Đường Cáp -
Đồ Thị Độ Biên Độ Dao Động Cực Đại Của Giỏ Phụ Thuộc H Và Nhận Xét: Với Các Hàm Hồi Quy Nhận Được Là Hàm Phi Tuyến, Từ Hàm Hồi Qui -
Nghiên cứu động lực học đường cáp vận chuyển trái thanh long ở vùng Tây Nam Bộ - 20 -
Nghiên cứu động lực học đường cáp vận chuyển trái thanh long ở vùng Tây Nam Bộ - 21
Xem toàn bộ 196 trang tài liệu này.
b) Thiết lập phương trình tương quan
Thiết lập phương trình tương quan dạng bậc 2:
a
2
2
f a a
0 1
Từ số liệu thực nghiệm trên bảng 4.5, bằng phương pháp bình phương nhỏ nhất, dẫn đếna = (a0 , a1. a2) sẽ là nghiệm của hệ phương trình đại số:
5a 12 103 a 292 105 a
126
0 1 2
12a 292 102 a 72 106 a
311,4
(4.12)
0 1 2
292 a 72 104a 179766 104a 7799,6
0 1 2
Giải ra ta được giá trị các hệ số của hàm hồi quy :
2
- Mô hình hồi quy: f = 204,5 - 0,174643. 
+ 4,1 10-5
(4.13)
Để kiểm tra tính đồng nhất của phương sai và tính tương thích của mô hình, lập bảng với số thí nghiệm n = 5, số lần thí nghiệm lặp r =3, số các hệ số cần xác định (trừ hệ số a0) : m = 2 ở bảng sau:
Trung bình | Hồi quy | Si2 | Sia2 | |
1 | 19.0 | 19.5 | 1.00 | 0.24 |
2 | 20.0 | 19.1 | 1.00 | 0.89 |
3 | 22.0 | 21.9 | 1.00 | 0.01 |
4 | 27.0 | 28.1 | 1.00 | 1.12 |
5 | 38.0 | 37.5 | 1.00 | 0.26 |
S2 = | 5.00 | Sa2 = 2,51 | ||
Max (Si2) = | 1.00 |
2 S 25
2 S 2
2,51
Có Sts 1 ; Sdu a 1,26
n 5 n m 1 2
Max( S 2 ) 1 S 2 1,26
Gtt i 0.2 ; Ftt du 1,26 ,
S
1
S 5
2 2
tt
Lấy mức độ chính xác của nghiên cứu = 0,05.
- Kiểm tra tính đồng nhất của phương sai:
Tra bảng phân vị Cochran C(r-1, n ,1-) = C(2 , 5 , 0.95) = 0,6638
=> Gb = 0,6638. Có Gtt = 0,2 < Gb = 0,6638 => Phương sai của thí nghiệm được coi là đồng nhất.
- Kiểm tra tính tương thích của phương trình hồi quy:
Tra bảng Fisher : F(n-m-1 , n(r-1), 1- ) = F(2 , 10 , 0.95) = 4,103
=> Fb = 4,103. Có Ftt = 1,26 < Fb = 4,103 => mô hình hồi quy là tương thích Từ kết quả thí nghiệm ở bảng 4.5 ta xây dựng được đồ thị tương quan giữa độ
vòng lớn nhất và chiều dài nhịp như hình 4.13.
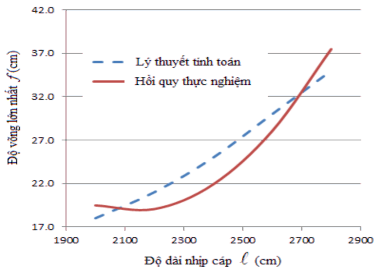
Hình 4.13. Đồ thị tương quan giữa độ vòng lớn nhất và chiều dài nhịp dây cáp
4.8.1.4. Ảnh hưởng của chiều dài nhịp cáp đến biên độ dao động giỏ đựng thanh long
a) Kết quả thí nghiệm
Đề tài đã tiến hành thí nghiệm như sau: Khoảng cách các giỏ treo trên nhịp cáp S = 80 cm; Cố định lực căng ngang H = 3000 N và tải trọng đều q = 0,2 N/cm, độ dài nhịp cáp thay đổi từ 2000 cm đến 2800 cm.
Số thí nghiệm n = 5 , số lần thí nghiệm lặp r =3.
Kết quả thí nghiệm đo dao động được được ghi ở bảng 4.6.
Bảng 4.6. Ảnh hưởng của chiều dài nhịp cáp đến biên độ dao động cực đại
Độ dài nhịp cáp (cm) | Biên độ lớn nhất tại giữa nhịp (cm) | |||||||
Lần 1 | Lần 2 | Lần 3 | Trung bình | Hồi quy thực nghiệm | Lý thuyết | Sai số % | ||
1 | 2000 | 22 | 23 | 24 | 23.0 | 23.3 | 21.0 | 11 |
2 | 2200 | 23 | 24 | 25 | 24.0 | 23.4 | 24.0 | 2 |
3 | 2400 | 26 | 25 | 24 | 25.0 | 25.1 | 27.0 | 7 |
4 | 2600 | 28 | 29 | 27 | 28.0 | 28.4 | 31.0 | 8 |
5 | 2800 | 34 | 33 | 33 | 33.5 | 33.3 | 35.0 | 5 |
b)Thiết lập phương trình tương quan
Thiết lập phương trình tương quan dạng bậc 2:
a
2
2
A a a
0 1
Từ số liệu thực nghiệm trên bảng 4.6, bằng phương pháp bình phương nhỏ nhất, dẫn đếna = (a0 , a1. a2) sẽ là nghiệm của hệ phương trình đại số :
5a 12 103 a 292 105 a
133.5
0 1 2
12a 292 102 a 72 106 a
325,4
(4.14)
0 1 2
292 a 72 104a 179766 104a 8040,8
0 1 2
Giải ra ta được giá trị các hệ số của hàm hồi quy :
2
- Mô hình hồi quy: A = 108,3 - 0,0818. 
+ 1,964.10-5
(4.15)
Để kiểm tra tính đồng nhất của phương sai và tính tương thích của mô hình, lập bảng với số thí nghiệm n = 5, số lần thí nghiệm lặp r =3, số các hệ số cần xác định (trừ hệ số a0): m = 2 ở bảng sau:
Trung bình | Hồi quy | Si2 | Sia2 | |
1 | 23.0 | 23.3 | 1.00 | 0.074 |
2 | 24.0 | 23.4 | 1.00 | 0.343 |
3 | 25.0 | 25.1 | 1.00 | 0.017 |
4 | 28.0 | 28.4 | 1.00 | 0.172 |
5 | 33.5 | 33.3 | 0.38 | 0.052 |
S2 = | 4.38 | Sa2 = 0.66 | ||
Max (Si2) = | 1.00 |
2 S 2
4,38
2 S 2
0,66
Có Sts 0,88 ; Sdu a 0,33
n 5 n m 1 2
Max( S 2 ) 1 S 2 0,88
Gtt i 0.2286 ; Ftt ts 2,66 ,
S
du
S 2 4,38 2 0,33
Lấy mức độ chính xác của nghiên cứu = 0,05.
- Kiểm tra tính đồng nhất của phương sai:
Tra bảng phân vị Cochran C(r-1, n ,1-) = C(2 , 5 , 0.95) = 0,6638
=> Gb = 0,6638. Có Gtt = 0,2286 < Gb = 0,6638 => Phương sai của thí nghiệm được coi là đồng nhất.
- Kiểm tra tính tương thích của phương trình hồi quy: Tra bảng Fisher : F(n-m- 1 , n(r-1), 1- ) = F(2 , 10 , 0.95) = 4,103 => Fb = 4,103. Có Ftt = 2,66 < Fb =
4,103 => mô hình hồi quy là tương thích
Từ kết quả thí nghiệm ở bảng 4.6 ta xây dựng được đồ thị tương quan giữa chiều dài nhịp với biên độ dao động lớn nhất của đường cáp như hình 4.14.
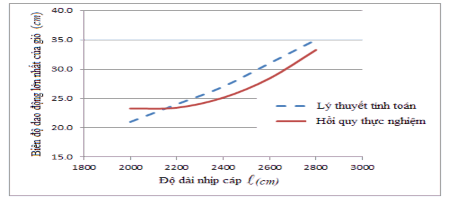
Hình 4.14. Đồ thị tương quan giữa biên độ dao động cực đại của giỏ treo tại giữa nhịp với chiều dài nhịp cáp 
(cm)
Kết luận: Từ kết quả thực nghiệm đơn yếu tố nhận được ở trên có một số kết luận sau:
- Ảnh hưởng của các tham số 
, H đến hàm chỉ tiêu là rò nét.
- Từ các hàm hồi qui và các đồ thị nhận được cho thấy tương quan hàm số giữa các hàm chỉ tiêu với tham số ảnh hưởng ở dạng phi tuyến.
- Từ kết quả thu được ở trên là căn cứ để chọn miền biến thiên của các tham số ảnh hưởng trong thí nghiệm đa yếu tố.
4.8.2. Kết quả thực nghiệm đa yếu tố
Kết quả thực nghiệm đơn yếu tố cho chúng ta thấy ảnh hưởng của từng tham số: 
và H vào hàm mục tiêu (f) chủ yếu là phi tuyến, theo 6 chúng tôi không tiến hành qui hoạch thực nghiệm bậc nhất mà thực hiện qui hoạch thực nghiệm bậc hai, các bước thực nghiệm đa yếu tố được tiến hành như sau:
4.8.2.1. Chọn vùng nghiên cứu và các giá trị biến thiên của thông số đầu vào
Từ kết quả thực nghiệm đơn yếu tố, chúng tôi chọn miền biến thiên của thông số đầu vào như sau:
- Đối với thông số lực căng ngang dây cáp H: Từ phương trình hồi qui (4.9), nhận thấy khi lực căng lớn thì độ vòng nhỏ, tuy nhiên lực căng lớn quá ảnh hưởng đến khả năng di động của đường cáp, độ bền của các chi tiết trong hệ thống, do vậy trong đề tài này chúng tôi chọn lực căng ngang của đường cáp từ 3 kN đến 5 kN.
- Đối với chiều dài nhịp 
: Từ phương trình hồi qui (4.13), và đồ thị hình 4.14 thấy rằng khi chiều dài nhịp tăng lên thì độ vòng tăng lên, khi độ vòng tăng lên ảnh hưởng đến khả năng vận chuyển trái thanh long, do vậy trong đề tài này chúng tôi chọn chiều dài nhịp từ 20 - 28 m. Mức thí nghiệm và giá trị mã hoá của thông số đầu vào ghi vào ở bảng 4.7.
- Để tránh các hệ số (trong hàm hồi quy ở dạng thực) quá nhỏ, nên các biến H và 
sẽ chọn đơn vị là : H (kN) và 
(m).
Bảng 4.7. Mức thí nghiệm của các thông số đầu vào
Giá trị mã | Các thông số vào | ||
X1 Lực căng ngang (kN) | X2 Chiều dài nhịp (m) | ||
Mức trên | 1 | 5 | 28 |
Mức cơ sở | 0 | 4 | 24 |
Mức dưới | -1 | 3 | 20 |
Khoảng biến thiên | 1 | 1 | 4 |
Trong đó X1, X2, là các giá trị mã hóa lần lượt của lực căng ngang H (kN) và chiều dài nhịp giữa hai puli 
(m).
4.8.2.2. Xây dựng ma trận thực nghiệm
Theo 6, chúng tôi đã chọn ma trận thực nghiệm theo kế hoạch trung tâm thực nghiệm trực giao với 2 thông số đầu vào và được trình bày ở bảng 4.8.
Bảng 4.8. Bảng ma trận thí nghiệm độ vòng f phụ thuộc lực căng ngang H và
chiều dài nhịp 
X1 | X2 | N1 | N1 | N3 | Trung bình TN | |
1 | -1 | -1 | 29 | 32 | 29 | 30.0 |
2 | 1 | -1 | 23 | 23 | 20 | 22.0 |
3 | -1 | 1 | 66 | 69 | 66 | 67.0 |
4 | 1 | 1 | 40 | 41 | 39 | 40.0 |
5 | -1 | 0 | 46 | 49 | 46 | 47.0 |
6 | 1 | 0 | 30 | 30 | 29 | 29.7 |
7 | 0 | -1 | 24 | 21 | 24 | 23.0 |
8 | 0 | 1 | 52 | 51 | 52 | 51.7 |
9 | 0 | 0 | 34 | 33 | 35 | 34.0 |
Bảng 4.9. Bảng ma trận thí nghiệm biên độ dao động cực đại của giỏ tại điểm treo giữa nhịp phụ thuộc lực căng ngang H và chiều dài nhịp 
X1 | X2 | N1 | N1 | N3 | TB | |
1 | -1 | -1 | 24 | 24 | 24 | 24.0 |
2 | 1 | -1 | 16 | 18 | 17 | 17.0 |
3 | -1 | 1 | 36 | 36 | 36 | 36.0 |
4 | 1 | 1 | 26 | 27 | 26 | 26.3 |
5 | -1 | 0 | 30 | 31 | 30 | 30.3 |
6 | 1 | 0 | 22 | 23 | 22 | 22.3 |
7 | 0 | -1 | 18 | 19 | 19 | 18.7 |
8 | 0 | 1 | 29 | 30 | 29 | 29.3 |
9 | 0 | 0 | 25 | 26 | 25 | 25.3 |
4.8.2.3. Kết quả thí nghiệm đa yếu tố
a) Kết quả thí nghiệm ảnh hưởng của lực căng ngang và chiều dài nhịp đến độ vòng đường dây cáp
Hàm hồi quy dạng mã mô tả quan hệ độ vòng f với lực căng ngang H và độ dài nhịp cáp 
có dạng :
a b b X
b X b X 2
b X X b X 2
(4.16)
f 1 2 1
3 2 4 1
5 1 2 6 2
Với số liệu thực nghiệm trên bảng 4.8, bằng phương pháp bình phương bé nhất, dẫn đến các hệ số trong (4.16) sẽ là nghiệm của phương trình đại số : M.Y = P, trong đó :
9 0 0 6 0 6
b1
344,3
0 6 0 0 0 0b 52,3
2
M 0 0 6 0 0 0B b3 P 83,7
6 0 0 6 0 4b 235,7
4
0 0 0 0 4 0
b5
19,0
6 0 0 4 0 6
b 233,7
Dẫn đến ma trận nghịch đảo M-1 sẽ là :
6
34,85
0.56 0 0 0.33 0
0.33
8,72
0 0.167 0 0 0 0
13,94
M 1
0 0 0.167 0 0 0
nên B = M-1. P =
0.33 0 0 0.5 0 0
3,06
4,75
0 0 0 0 0.25 0
0.33 0 0 0 0 0.5
Do đó có được :
2,06
2 2
1 2 2
af 34,85 8,72X1 13,94X2 3,06X1 4,75X X 2,06X
(4.17)
Để kiểm tra tính đồng nhất của phương sai và tính tương thích của mô hình, lập bảng với số thí nghiệm n = 9, số lần thí nghiệm lặp r =3, số các hệ số cần xác định (trừ hệ số b0): m = 5 ở bảng sau:
Trung bình TN | Hồi quy | Si2 | Sia2 | |
1 | 30.0 | 30.0 | 3.00 | 0.00 |
2 | 22.0 | 22.0 | 3.00 | 0.00 |
3 | 67.0 | 67.4 | 3.00 | 0.14 |
4 | 40.0 | 40.4 | 1.00 | 0.19 |
5 | 47.0 | 46.6 | 3.00 | 0.14 |
6 | 29.7 | 29.2 | 0.33 | 0.23 |
7 | 23.0 | 23.0 | 3.00 | 0.00 |
8 | 51.7 | 50.9 | 0.33 | 0.66 |
9 | 34.0 | 34.9 | 1.00 | 0.73 |
S2 = | 17.67 | 2.1 | ||
Max Si2= | 3.00 | Sa2 |
2 S2
17,67
2 S 2
2,1
Có Sts 1,96 ; Sdu a 0,7
n 9 n m 1 3
Max( S 2 ) 3 S 2 1,96
Gtt i 0.17 ; Ftt ts 2,81
S
du
S 2 17,67 2 0,7
Lấy mức độ chính xác của nghiên cứu = 0,05
- Kiểm tra tính đồng nhất của phương sai:
Tra bảng phân vị Cochran C(r-1, n ,1-) = C(2 , 9 , 0.95) = 0,477
=> Gb = 0,477. Có Gtt = 0,17 < Gb = 0,477 => Phương sai của thí nghiệm được coi là đồng nhất.
- Kiểm tra tính tương thích của phương trình hồi quy:
Tra bảng Fisher : F(n-m-1 , n(r-1), 1- ) = F(3 , 18 , 0.95) = 3,16
=> Fb = 3,16. Có Ftt = 2,81 < Fb = 3,16 => mô hình hồi quy là tương thích.
(Tính hàm Fisher trong EXCEL theo hàm FINV(0.05, n-m-1, n(r-1))
- Kiểm tra mức ý nghĩa của các hệ số mô hình toán:
Theo tiêu chuẩn Student, các hệ số trong mô hình (4.16) có khoảng sai lệch với tin cậy ( 1) là :