Các Tính Chất Của Ước Lượng Điểm

Rò ràng

thống kê.

$f x1,x2,..., xn

là một hàm của các giá trị mẫu hay còn gọi là một

Ví dụ 3.10. X , S2 , s2 là những thống kê.

3.2.2. Các tính chất của ước lượng điểm

Do giá trị đúng của  chưa biết nên ta không thể so sánh $với  để đánh giá chất lượng của$. Vì vậy người ta đưa ra các tính chất sau:

a. Ước lượng không chệch

Định nghĩa: Thống kê $được gọi là ước lượng không chệch của  nếu E$= 

Ngược lại, nếu E$ thì $được gọi là ước lượng chệch của .

Ý nghĩa: Ta thấy E($-  ) = 0, tức là trung bình của độ lệch (sai số) giữa các ước lượng với giá trị thật bằng 0.

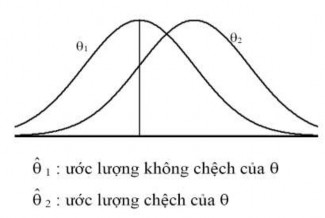
Hình 3.1: Ước lượng chệch, ước lượng không chệch

Ví dụ 3.11.

- Vì E( X ) =  nên trung bình mẫu là ước lượng không chệch của kỳ vọng (trung bình tổng thể) .

- Vì E(s2) = 2 nên phương sai mẫu hiệu chỉnh là ước lượng không chệch của phương sai tổng thể 2.

- S2 là ước lượng chệch của VX với độ chệch là

2 .

n

Ví dụ 3.12. Cân 100 sản phẩm của xí nghiệp ta có bảng sau:

xi (gr)

498	502	506	510
ni	40	20	20	20

Có thể bạn quan tâm!

• Lý thuyết xác suất và thống kê toán - 8
• Lý thuyết xác suất và thống kê toán - 9
• Lý thuyết xác suất và thống kê toán - 10
• Khoảng Tin Cậy Cho Phương Sai Trong Trường Hợp K Ỳ Vọng  Đã Biết
• Lý thuyết xác suất và thống kê toán - 13
• Bài Toán 1 : Phương Sai Vx = Σ 2 Đã Biết

Xem toàn bộ 168 trang tài liệu này.

Ta có trung bình mẫu là:

x  498.40  502.20  506.20  510.20  502,8 (gr)

100

Theo nhận xét trên ta dự đoán (ước lượng) trọng lượng trung bình của sản phẩm trong xí nghiệp là  = 502,8 (gr).

b. Ước lượng vững



Định nghĩa: Thống kê $(x1, x2, . . . , xn) được gọi là ước lượng vững của  nếu $hội tụ theo xác suất đến  khi n , tức là

 0 lim P | $| 1

n

Ý nghĩa: Với n đủ lớn thì với xác suất gần bằng 1 ta có thể xấp xỉ: $= 

Ví dụ 3.13.

- Trung bình mẫu X là ước lượng vững của trung bình tổng thể .

- Phương sai mẫu hiệu chỉnh s2 là ước lượng vững của phương sai tổng thể

2.

c. Ước lượng hiệu quả

Định nghĩa: Thống kê $được gọi là ước lượng hiệu quả của  nếu nó là ước lượng không chệch của  và có phương sai bé nhất trong tất cả các ước lượng không chệch của .

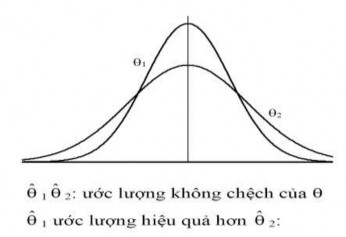
Hình 3.2: Ước lượng hiệu quả

Ví dụ 3.14. Nếu biến ngẫu nhiên X :

hiệu quả của kỳ vọng EX 

3.3. Ước lượng khoảng

N ,2 

thì trung bình mẫu X là ước lượng

3.3.1. Khái niệm ước lượng khoảng

Ước lượng điểm có một nhược điểm cơ bản là không thể biết được độ chính xác cũng như xác suất để ước lượng đó chính xác. Nhất là khi kích thước mẫu nhỏ sự sai lệch của ước lượng với giá trị thật khá lớn và chỉ với một số rất khó đánh giá được khả năng mắc sai lầm khi ước lượng là bao nhiêu.

Để khắc phục hạn chế đó, người ta dựa vào ước lượng bằng một khoảng giá trị. Để ước lượng một tham số , người ta xây dựng một thống kê nào đó có luật phân phối xác định không phụ thuộc vào . Nếu dựa vào thống kê đó ta tìm được khoảng

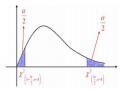
giá trị 1;2

trong đó 1,2

phụ thuộc vào thống kê trên, sao cho với một xác suất

cho trước tham số rơi vào khoảng 1;2

tức là

P12 1

1;2: gọi là khoảng tin cậy

1: gọi là độ tin cậy

: gọi là mức ý nghĩa

2 1  2: gọi là độ dài của khoảng tin cậy

: gọi là độ chính xác của ước lượng Để làm điều đó quy tắc chung như sau:

Đầu tiên tìm một thống kê

G  G(x1, x2 ,..., xn , )

sao cho phân phối của G xác

định hoàn toàn (không chứa tham số nữa).

Khi đó với độ tin cậy 1cho trước, ta tìm cặp giá trị

1 và 2

sao cho

1 2 (để ý chúng đều dương) và tương ứng với chúng là các phân vị gvà g1

thỏa mãn điều kiện:

1

P(G  g) 1 và

1 2

2

P(G  g1) 2

Suy ra: P(g G(x1, x2 ,..., xn )  g1

) 11 2 1.

1 2

P(1 2 )  1

3.3.2. Khoảng tin cậy cho kỳ vọng

Giả sử biến ngẫu nhiên X :

N ;2 

và tham số chưa biết, ngoài ra ta

biết được mẫu quan sát của X là (x1 , x2 , . . . , xn) . Bài toán đặt ra là: tìm khoảng tin

cậy cho EX 

với độ tin cậy 1

cho trước. Ta xét 2 trường hợp sau:

a. Bài toán 1: Phương sai VX = 2 của biến X đã biết

X n

Để ước lượng khoảng cho kỳ vọng EX =  với độ tin cậy 1 – , ta chọn thống kê:

G  U 



Khi đó ta có: U ~ N(0, 1)

Chọn cặp

1 và

2 sao cho

1 2 .

Do phân vị chuẩn

u1, ucó tính chất

u1

u

nên ta có:

1 2 1 2

P(u U  u)  1

1 2



P X  u X  u 1

n

n

2 1 

Suy ra: với độ tin cậy 1 – α, khoảng tin cậy cho kỳ vọng là:

n

x 

u2

 x 



n

u1

Như vậy với độ tin cậy 1cho trước ta sẽ có vô số cặp với vô số khoảng tin cậy. Ta xét một số trường hợp đặc biệt:

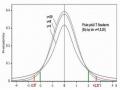
* Khoảng tin cậy đối xứng (ứng với ) là:

1 2 2

( x -  ; x +  ) hoặc viết  = x ± 𝜀

1 và

2 , tương ứng

trong đó:

 =



n

.u(độ chính xác của ước lượng).

2

1 k

n

x xini i1

là trung bình mẫu hay kỳ vọng mẫu

Tra bảng Laplace, tìm u

với  u  1 ;



2 â  2

* Khoảng tin cậy trái (ứng với 1 , 2  0 ) là: ( ; x +



n

.u)

trong đó: u 1 , tra bảng Laplace  uα= ?

n

1 2

* Khoảng tin cậy phải (ứng với  0, ) là: ( x 

.u

; + )

* Quy tắc tìm khoảng tin cậy đối xứng cho kỳ vọng (2 đã biết)

- Từ mẫu cụ thể tính x .

- Tính các phân vị u từ công thức (u )  1

(tra bảng Laplace)



2 2

n

- Tính độ chính xác của ước lượng: 

2

u .

2

- Khoảng tin cậy cho kỳ vọng tổng thể: ( x -  ; x +  ).

Tương tự như vậy đối với quy tắc tìm khoảng tin cậy trái và khoảng tin cậy phải cho kỳ vọng.

Ví dụ 3.15. Trọng lượng của một loại sản phẩm là biến ngẫu nhiên có phân phối chuẩn với độ lệch tiêu chuẩn là 1 gam. Cân thử 25 sản phẩm loại này, thu được kết quả sau:

Trọng lượng (gam)

18	19	20	21
Số sản phẩm tương ứng	3	5	15	2

Với độ tin cậy 95%, hãy tìm khoảng ước lượng của:

a) Trọng lượng trung bình của 1 sản phẩm;

b) Trọng lượng trung bình tối thiểu của một sản phẩm. Giải

của .

Gọi là trọng lượng trung bình của sản phẩm, ta cần ước lượng khoảng tin cậy

Trọng lượng trung bình của mẫu 25 sản phẩm: x = 19,64

a) Khoảng tin cậy đối xứng cho trọng lượng trung bình sản phẩm.

Với độ tin vậy 95% ta tìm được

u như sau:

2

2

2

(u )  1 10, 05  0,975 Tra bảng 3 ta được u = 1,96.

n

2 2

Độ chính xác của ước lượng là:



u 1 .1,96  0,392

5



2

gam.

Khoảng tin cậy phải cho trọng lượng trung bình của sản phẩm:

( x -  ; x +  ) = (19,64 - 0,392; 19,64 + 0,392) = (19,248; 20,032)

Vậy trọng lượng trung bình của một sản phẩm khoảng từ 19,248 đến 20,032

b) Khoảng tin cậy phải cho trọng lượng trung bình sản phẩm.

Với độ tin vậy 95% ta tìm được unhư sau:

(u)  1 1 0, 05  0,95

Tra bảng 3 ta được u= 2,58

n

Độ chính xác của ước lượng: 

u 1 .1, 65  0,33

5

Khoảng tin cậy phải trọng lượng trung bình của sản phẩm: ( x -  ; ) = (19,64 - 0,33; ) = (19,31; )

Vậy trọng lượng trung bình tối thiểu của một sản phẩm là 19,31gam.

b. Bài toán 2: Phương sai VX = 2 của biến X chưa biết

Đầu tiên ta phải ước lượng 2 bằng phương sai mẫu hiệu chỉnh, sau đó chọn

thống kê

G  T  . Khi đó T tuân theo luật Student với n -1 bậc tự do, mặt

X n

s

khác hình dạng của mật độ phân phối này rất gần với phân phối chuẩn, nên cách ước lượng rất giống với bài toán 1.

Ta tìm phân vị

t, t1

;(t1

t) thỏa mãn:

P(t

 T  t

)  1

1 2 1 1 1 2

Tương tự như bài toán 1, ta xét một số khoảng tin cậy đặc biệt:

* Khoảng tin cậy đối xứng là: ( x -  ; x +  ) hoặc viết  = x ± 𝜀

trong đó:  =

s .t

n



2

là độ chính xác của ước lượng;

1

k

x 

n i1

xi ni

là trung bình mẫu;

s là độ lệch mẫu hiệu chỉnh;

Tra bảng Student (bảng 5), tìm

t với:

t  t



1

n1 

2

n



* Khoảng tin cậy trái là: ( ; x + s .t )

2 2 

trong đó: t= tn-1(1 – ) tra bảng Student (bảng 5) tìm được t

n

* Khoảng tin cậy phải là: ( x 

s .t

; )



Chú ý: Nếu n  30 thống kê T sẽ có phân phối tiệm cận chuẩn N(0; 1), việc tìm khoảng ước lượng với độ tin cậy 1được làm giống như bài toán 1, với được thay thế bằng s.

* Quy tắc tìm khoảng tin cậy đối xứng cho kỳ vọng (2 chưa biết)

- Từ mẫu cụ thể tính x , s

- Tính các phân vị t

từ công thức t  t

1

n1 2 

2

2

- Tính độ chính xác của ước lượng: 



n



s t

2

- Khoảng tin cậy cho kỳ vọng tổng thể: ( x -  ; x +  ).

Tương tự như vậy đối với quy tắc tìm khoảng tin cậy trái và khoảng tin cậy phải cho kỳ vọng.

Ví dụ 3.16. Ở một cửa hàng chế biến thủy sản, theo dòi lượng nước mắm bán ra trong một số ngày, người ta ghi được bảng số liệu sau.

Số lượng bán ra (lít)

Số ngày
20 – 30	3
30 – 40	8
40 – 50	30
50 – 60	45
60 – 70	20
70 – 80	25
80 – 90	17
90 – 100	9
> 100	4

Hãy ước lượng số lít nước mắm bán ra trung bình mỗi ngày với độ tin cậy 99% trong hai trường hợp:

a) biết phương sai 2 = 132,25;

b) chưa biết phương sai. Giải

Ta lập bảng tính các đặc trưng của mẫu:

Số lượng bán ra (lít)

xi	ni	xini	x2n i i
20 – 30	25	3	75	1875
30 – 40	35	8	280	9800
40 – 50	45	30	1350	60750
50 – 60	55	45	2475	136125
60 – 70	65	20	1300	84500
70 – 80	75	25	1875	140625
80 – 90	85	17	1445	122825
90 – 100	95	9	855	81225
> 100	105	4	420	44100
		161	10075	681825

Ta có:

X 10075 = 62, 5776 ;

161

X 2 681825 = 4234,9379 ;

161

S2 = 318,9819  s2= 320,9755  s = 17,9158

(có thể dùng máy tính bỏ túi để tính đặc trưng mẫu trên mà không cần lập bảng trên) Với 1 – α = 99% ta có uα/2 = 2,58 (tra bảng 3)

a) Theo đề bài, phương sai của tổng thể đã biết

2 = 132,65  = 11,5174.

n

Do đó:  = uα/2

σ = 2,58 .

11,5174 = 2,3419.

161

Vậy, số lít nước mắm bán ra trung bình mỗi ngày ở cửa hàng đó là

 = X  = 62,5776  2,3419.

hay

60,2357  64,9195 (lít).

b) Phương sai của tổng thể chưa biết, n  30 nên độ chính xác là

n

 = uα/2

S = 2,58 .

17,9158 = 3,6429.

161

Vậy  = 62,5776  3,6429 (lít).

Ví dụ 3.17. Cân ngẫu nhiên 25 bao xi măng trên thị trường ta thu được bảng kết quả sau:

Trọng lượng (kg)	47	48	49	50	51	52	53
Số bao	2	3	4	6	5	3	2

Với độ tin cậy 95%, tìm khoảng tin cậy cho trọng lượng trung bình bao xi

măng, biết trọng lượng X của bao xi măng tuân theo luật phân phối chuẩn với chưa biết.

Giải

N(2 ,

Sử dụng máy tính điện tử tính được: x  50,04 ; s  1,6951

Tra bảng Student ta có

t  t24 (0,975)  2,0639

2

Độ chính xác của ước lượng: 1, 6951 2, 0639  0, 6997

25

Khoảng tin cậy là: (x ; x ) 49,3404; 50,7397

Vậy với độ tin cậy 95% một bao xi măng bán trên thị trường có trọng lượng từ 49,3403 đến 50,7397 (kg).

c. Bài toán 3: tìm kích thước mẫu, độ tin cậy của ước lượng

Trường hợp 1: Xác định kích thước mẫu n tối thiểu để độ chính xác của ước lượng

n



s u

2

không vượt quá số 0

cho trước?

Có nghĩa ta cần xác định n sao cho:

s s 2

n

u 0  n 

u 

2 0 2 

Vậy n được xác định bằng công thức:

s

2 



n 



u 

0 2 

 1



trong đó .là phần nguyên. Chú ý:

- Do s lại phụ thuộc vào n, để khắc phục điều này ta lấy một mẫu sơ bộ (x1,

x2, ... , xm) với kích thước m > 30 nào đó và tính s theo mẫu đó. Chúng ta có thể lấy ngay mẫu mà trong đề bài đã cho.

- Trong công thức xác định n trên, nếu đã biết thì ta thay độ lệch mẫu s bởi . Trường hợp 2: Cho biết độ chính xác của ước lượng và trung bình mẫu x . Xác định độ tin cậy của ước lượng.