Bài Toán 1 : Phương Sai Vx = Σ 2 Đã Biết

CHƯƠNG 4: KIÓM ®ÞNH GI¶ THUYÒT THỐNG Kª

4.1. Giả thuyết thống kê

Trong nhiều lĩnh vực đời sống kinh tế - xã hội, chúng ta hay đưa ra những nhận xét khác nhau về các đối tượng quan tâm. Những nhận xét như vậy thường được gọi là các giả thuyết, chúng có thể đúng có thể sai. Vấn đề xác định đúng sai của giả thuyết sẽ được gọi là kiểm định.

Trong thống kê, chúng ta xuất phát từ một mẫu

x1, x2 ,..., xn

chọn từ tập nền chưa

biết phân phối hoặc có phân phối

F x,

nhưng chưa biết tham số . Ta có thể có

nhiều nhận xét khác nhau về các yếu tố chưa biết – đó là các giả thuyết thống kê.

Giả thuyết được đưa ra kiểm định được gọi là giả thuyết gốc, ký hiệu là H0; các giả thuyết khác với H0 được gọi là giả thuyết đối hay đối thuyết, ký hiệu là H1.

Ta thừa nhận khi đã chọn cặp H0, H1 thì việc chấp nhận H0 chính là bác bỏ H1 và ngược lại. Việc kiểm định một giả thuyết là đúng hay sai dựa trên thông tin mẫu được gọi là kiểm định giả thuyết thống kê.

Ví dụ 4.1. Khi nghiên cứu thu nhập của cán bộ, nhân viên một công ty nào đó, ta có thể đưa ra nhiều giả thuyết khác nhau:

H0: Thu nhập trung bình của mỗi người trong công ty là 60 triệu đồng/ năm H1: Thu nhập trung bình của mỗi người trong công ty khác 60 triệu đồng/ năm

hoặc

H0: Thu nhập trung bình của mỗi người trong công ty là 60 triệu đồng/ năm H1: Thu nhập trung bình của mỗi người trong công ty trên 60 triệu đồng/ năm

hoặc

H0: Thu nhập trung bình của mỗi người trong công ty là 60 triệu đồng/ năm H1: Thu nhập trung bình của mỗi người trong công ty dưới 60 triệu đồng/ năm

4.2. Quy tắc kiểm định

Nguyên tắc chung của kiểm định giả thuyết thống kê là dựa trên nguyên lý xác suất nhỏ: một sự kiện có xác suất xuất hiện khá bé thì có thể coi như nó không xảy ra khi thực hiện phép thử, tuy nhiên trong thực tế vấn đề phức tạp hơn rất nhiều.

4.2.1. Tiêu chuẩn kiểm định

Tiêu chuẩn kiểm định phải được xây dựng đơn giản và dựa trên các thông tin

mẫu

x1, x2 ,..., xn . Thông thường, người ta chọn một thống kê

KK x1,x2,..., xn

Có thể phụ thuộc vào tham số đã biết trong giả thuyết H0, nếu giả thuyết H0 đúng thì luật phân phối của K phải hoàn toàn xác định. Một thống kê như vậy gọi là tiêu chuẩn kiểm định.

4.2.2. Quy tắc kiểm định

Nếu miền xác định của trong đó:

w: là miền bác bỏ H0

KK x1,x2,..., xn

được chia thành 2 miền w, w

w: là miền chấp nhận H0

Như vậy, nếu ta dùng quy tắc kiểm định như trên thì có thể mắc phải hai loại sai lầm sau:

Sai lầm loại 1: trên thực tế giả thuyết H0 đúng nhưng qua kiểm định, ta lại kết luận giả thuyết H0 sai.

Sai lầm loại 2: trên thực tế giả thuyết H0 sai nhưng qua kiểm định, ta lại kết luận giả thuyết H0 đúng.

4.3. Các dạng miền tới hạn

Trong thực tế, người ta chọn miền tới hạn của tiêu chuẩn K phụ thuộc vào cặp giả thuyết và đối thuyết H0, H1 như sau:

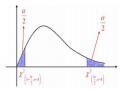
4.3.1. Kiểm định đối xứng



H0 :0

Ta chọn các phân vị

Kvà

1 :0



K sao cho :

1



P K K2 ; P K K2

2 

2 



Khi đó miền bác bỏ H0 là w; KK; 

2 2 



KK

1

2 2

Hình 4.1: Miền bác bỏ giả thuyết của kiểm định đối xứng

4.3.2. Kiểm định trái



H0 :0

1 :0

Ta chọn các phân vị Ksao cho :

P K K

Khi đó miền bác bỏ H0 là

w; K



K

Hình 4.2: Miền bác bỏ giả thuyết của kiểm định trái

4.3.3. Kiểm định phải



H0 :0

1 :0

Ta chọn các phân vị

K1

sao cho :

P K K1

Khi đó miền bác bỏ H0 là

wK1;



K1

Hình 4.3: Miền bác bỏ giả thuyết của kiểm định phải

4.4. Kiểm định về kỳ vọng

Giả sử mẫu x1, x2, ... xn được chọn từ biến ngẫu nhiên gốc X có phân phối chuẩn

N(, 2 )

và μ0 là giá trị cho trước. Bài toán đặt ra là với mức ý nghĩa ( hay độ

tin cậy 1

) cho trước, hãy kiểm định giả thuyết

H0 :  = 0

Ta xét 2 trường hợp sau:

4.4.1. Bài toán 1: Phương sai VX = σ2 đã biết

(X 0 ) n

Chọn thống kê: K 

làm tiêu chuẩn kiểm định.

(x 0 )

Từ mẫu cụ thể tính x và tính giá trị kiểm định:

K 



a. Kiểm định hai phía (hay kiểm định đối xứng) Kiểm định giả thuyết:

H0 : 0

H : 

1 0

Nếu H0 đúng thì K ~ N(0,1) xác định hoàn toàn. Do đó với mức ý nghĩa cho

trước, xác định phân vị chuẩn

u .

Ta tìm được miền bác bỏ H

là: W

; u 



0  U  u ; 

Thật vậy:

2 2 



P U  W P U u  P U  u 

2 2 



 2P  U  u  2  2P  U  u 

2 2 

 2 2 

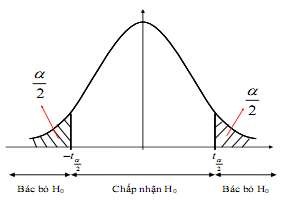
Hình 4.4: Miền bác bỏ giả thuyết của kiểm định đối xứng

b. Kiểm định phía trái

H0 : 0

H : 

1 0

Với mức ý nghĩa cho trước, xác định phân vị chuẩn u. Ta tìm được miền bác bỏ H0 là:

W ;  u

Hình 4.6: Miền bác bỏ giả thuyết của kiểm định trái

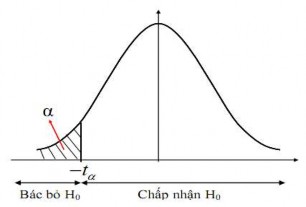
c. Kiểm định phía phải

H0 : 0

H : 

1 0

Với mức ý nghĩa cho trước, xác định phân vị chuẩn u. Ta tìm được miền bác bỏ H0 là:

Wu;

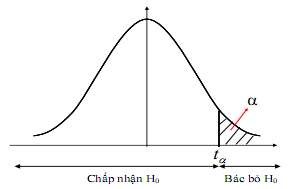
Hình 4.5: Miền bác bỏ giả thuyết của kiểm định phải

Ví dụ 4.2. Một hãng bảo hiểm ô tô thông báo rằng số tiền trung bình hãng chi trả cho khách hàng bị tai nạn giao thông là 8500 đôla trong một năm. Người ta kiểm tra ngẫu nhiên hồ sơ chi trả của 25 trường hợp thì thấy trung bình mẫu là 8900 đô la. Giả sử

rằng số tiền chi trả tuân theo luật phân phối chuẩn với  2600 , hãy kiểm định thông

báo của hãng bảo hiểm trên với mức ý nghĩa  0, 05 .

Giải

H0 :  8500

H :  8500

1

Hàm kiểm định:

K  8900  8500 25  0, 77

2600

Với mức ý nghĩa  thì

u  1,96 .

Miền bác bỏ giả thuyết là

W, 1,961,96, 

Suy ra

K u

, vậy K  W

Ta không có cơ sở đề bác bỏ thông báo của hãng bảo hiểm.

Ví dụ 4.3. Mỳ chính được đóng gói 500 gam một gói trên máy tự động. Có thể coi trọng lượng các gói mỳ chính tuân theo luật phân phối chuẩn với độ lệch chuẩn 36 gam. Kiểm tra ngẫu nhiên 81 gói thấy trọng lượng trung bình 498 gam. Với mức ý nghĩa 5% có thể cho kết luận trọng lượng gói mỳ chính bị đóng thiếu không?

Giải

H0 :  500

H :  500

1

x 0

498  500 81

Từ mẫu 81 gói ta thu được x  498 gam . Hàm kiểm định:

K 0,5

 36

Với mức ý nghĩa  thì u 1,645 .

Miền bác bỏ giả thuyết H0:

W; 1, 645

Ta thấy K  W

nên chưa đủ cơ sở để kết luận trọng lượng trung bình của các

gói mỳ chính bị đóng thiếu.

4.4.2. Bài toán 2: Phương sai VX = σ2 chưa biết

X 0 

Chọn thống kê

K làm tiêu chuẩn kiểm định.

Từ mẫu cụ thể tính x , s và tính giá trị hàm kiểm định:

a. Kiểm định hai phía

K  (x 0 ) n s

H0 : 0

H : 

1 0

Nếu H0 đúng thì K ~ T(n 1) . Do đó với mức ý nghĩa đã cho, ta xác định

phân vị Student (n -1) bậc tự do mức 1

là:

t  tn1 (1 )

Khi đó miền bác bỏ là:

W

; t  U  t ; 



2 2 

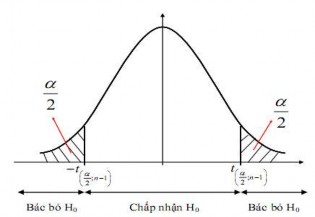
Hình 4.7: Miền bác bỏ giả thuyết của kiểm định hai phía

c. Kiểm định phía trái

H0 : 0

H : 

1 0

Với mức ý nghĩa cho trước, giá trị phân vị Student được thay bằng

t

Khi đó miền bác bỏ là:

c. Kiểm định phía phải

 tn1 (1)

W ; t

H0 : 0

H : 

1 0

Với mức ý nghĩa cho trước, giá trị phân vị Student được thay bằng:

t

Khi đó miền bác bỏ là:

 tn1 (1)

Wt; 

Chú ý: Khi n  30 thống kê T sẽ có phân phối tiệm cận chuẩn N(0; 1), việc tìm khoảng ước lượng với độ tin cậy 1được làm giống như bài toán 1, với được thay thế bằng s.

Ví dụ 4.4. Một cửa hàng nhận thấy lâu nay trung bình mỗi khách hàng mua 15 ngàn đồng. Tuần này cửa hàng chọn ngẫu nhiên 16 khách hàng thì thấy trung bình mỗi người mua 14 ngàn đồng và độ lệch mẫu hiệu chỉnh là 2 ngàn đồng. Cho biết sức mua của khách hàng có phân phối chuẩn. Với mức ý nghĩa 5%, xét xem sức mua của khách hàng có giảm sút không ?

Giải

H0 :  15000

H :  15000

1

Hàm kiểm định: K = 14 - 15 16

= 2.

Vì kích thước mẫu n = 16 < 30 nên tra bảng phân phối Student dòng 15 cột  = 0,05 ta được:

Miền bác bỏ: W (;

t= 2,131.

 2,132)

Suy ra: K  W

. Vậy sức mua của khách hàng không giảm sút.

Ví dụ 4.5. Trọng lượng của các bao gạo là đại lượng ngẫu nhiên có phân phối chuẩn với trọng lượng trung bình là 50kg. Sau một khoảng thời gian hoạt động người ta nghi ngờ trọng lượng các bao gạo có thay đổi. Cân 25 bao gạo thu được các kết quả sau:

Khối lượng

40-48,5	48,5-49	49-49,5	49,5-50	50-50,5
Số bao	2	5	10	6	2