Miền bác bỏ là
W; 2, 797U2, 797;
Ta thấy K W
nên nghi ngờ của khách hàng là đúng.
Ví dụ 4.6. Một nhóm nghiên cứu tuyên bố rằng trung bình một người vào siêu thị X tiêu hết 300 nghìn đồng. Chọn một mẫu ngẫu nhiên gồm 50 người mua hàng, tính được số tiền trung bình họ tiêu là 315 nghìn đồng với độ lệch mẫu hiệu chỉnh s 42 . Với mức ý nghĩa 0,02 hãy kiểm định xem tuyên bố trên có đúng không?
Giải
H0 : 300
H : 300
1
Có thể bạn quan tâm!
-
Khoảng Tin Cậy Cho Phương Sai Trong Trường Hợp K Ỳ Vọng Đã Biết -
Lý thuyết xác suất và thống kê toán - 13 -
Bài Toán 1 : Phương Sai Vx = Σ 2 Đã Biết -
Kiểm Định Sự Bằng Nhau Của 2 Tỷ Lệ -
Không Thể Kết Luận Học Sinh Nội Thàn Có Thể Lực Tốt Hơn -
Công Thức Ước Lượng Hệ Số Của Đường Hồi Quy Tuyến Tính
Xem toàn bộ 168 trang tài liệu này.
Hàm kiểm định
K 2,525
x 0
n
315 300 50
s 42
Ta có n = 50 > 30. Độ tin cậy 1 – α = 0,98 1 – α/2 = 0,99
Tra bảng phân phối chuẩn, ta được:
u 2, 33.
2
Miền bác bỏ là
W; 2,33U2,33;
Ta thấy K W
nên tuyên bố trên không đúng.
4.5. Kiểm định phương sai
Giả sử mẫu x1, x2, ... xn được chọn từ biến ngẫu nhiên gốc X có phân phối chuẩn
N(, 2 )
và μ0 là giá trị cho trước. Bài toán đặt ra là với mức ý nghĩa ( hay độ tin
0
cậy 1) cho trước, hãy kiểm định giả thuyết H0 : VX 2 .
Ta xét 2 trường hợp sau:
4.5.1. Bài toán 1: Kỳ vọng EX đã biết
Để kiểm định giả thuyết trên ta dùng thống kê
n
2
xi0
2
K i1
0
a. Kiểm định hai phía
H : 22
0 0
H : 2 2
1 0
Nếu H0 đúng thì K ~ 2 (n 1) . Miền bác bỏ H0 là:
n 2 n 2
xi0xi0
Wi1;i1
2 n, 2 n,1
2 2
b. Kiểm định phía trái
H : 22
0 0
H : 2 2
1 0
Miền bác bỏ H0 là:
c. Kiểm định phía phải
W ;2n 1,
H : 22
0 0
H : 2 2
1 0
Miền bác bỏ H0 là:
W 2n 1,1;
4.5.2. Bài toán 1: Kỳ vọng EX chưa biết
Để kiểm định giả thuyết trên ta dùng thống kê
n1s2
2
K
0
a. Kiểm định hai phía
H : 22
0 0
H : 2 2
1 0
n1s2n1s2
Miền bác bỏ H0 là:
W;
;
2 n, 2 n,1
2 2
b. Kiểm định phía trái
H : 22
0 0
H : 2 2
1 0
Miền bác bỏ H0 là:
c. Kiểm định phía phải
W ;2n 1,
H : 22
0 0
H : 2 2
1 0
Miền bác bỏ H0 là:
W 2n 1,1;
Ví dụ 4.7. Chủ hãng sản xuất một loại thiết bị đo cho biết độ lệch chuẩn của sai số đo là 5 mm ( tuân theo luật phân phối chuẩn ). Kiểm tra một mẫu gồm 19 thiết bị đo thấy
s2 33mm2 . Với mức ý nghĩa 0, 05
a) Có thể kết luận gì về ý kiến của chủ hãng?
b) Có ý kiến khác cho rằng độ lệch chuẩn của sai số đo lớn hơn 5 mm. Hãy kiểm định ý kiến đó.
Giải a)
H : 2 25
1
0
n1s218.33
H : 2 25
K 23, 76
0
2 25
Với mức ý nghĩa 0, 05 , ta có
2 18;0, 025 8, 2; 2 18;0,975 31,5
Suy ra
W;8, 231,5; K W
vậy ý kiến của chủ hãng có thể
chấp nhận được. b)
H : 2 25
1
0
n1s218.33
H : 2 25
K 23, 76
0
2 25
Với mức ý nghĩa 0, 05 , ta có
2 18;0,975 28,9
Suy ra W28,9; K W
Vậy ý kiến cho rằng độ lệch chuẩn của sai số đo lớn hơn 5 mm là sai.
4.6. Kiểm định về tỷ lệ
Với mức ý nghĩa ( hay độ tin cậy 1) cho trước, hãy kiểm định giả thuyết
H0 : p p0
Biết rằng p là tham số của phân phối
B 1; p
. Nếu n lớn và p không quá
gần 0, 1 thì phân phối chuẩn có thể được dùng để xấp xỉ phân phối nhị thức
B n; p.
(f p0 ) n
p0 (1 p0 )
Chọn thống kê: K làm tiêu chuẩn kiểm định.
4.6.1. Kiểm định hai phía
H0 : p p0
H : p p
1 0
Nếu H0 đúng thì K ~ N(0, 1). Do đó với mức ý nghĩa , ta xác định được giá trị
u
phân vị
sao cho:
2
P | K |
u
2
Suy ra miền bác bỏ H0 là:
W; u U u ;
2 2
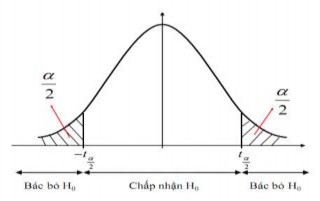
Hình 4.8: Miền bác bỏ giả thuyết trong kiểm định hai phía về tỷ lệ
4.6.2. Kiểm định phía trái
H0 : p p0
H : p p
1 0
Với mức ý nghĩa , xác định giá trị tới hạn utheo công thức u 1.
Vì PU usuy ra miền bác bỏ H0 là:
W ( ; u)
u
Hình 4.9: Miền bác bỏ giả thuyết trong kiểm định phía trái về tỷ lệ
4.6.3. Kiểm định phía phải
H0 : p p0
H : p p
1 0
Với mức ý nghĩa , xác định giá trị tới hạn utheo công thức
u 1. Vì
PK usuy ra miền bác bỏ H0 là:
W (u;
)
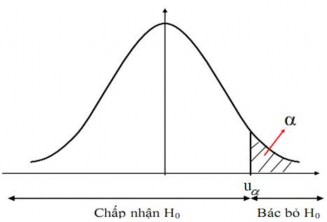
Hình 4.10: Miền bác bỏ giả thuyết trong kiểm định phía phải về tỷ lệ
Ví dụ 4.8. Chủ một tờ báo thông báo có 25 % độc giả thường xuyên là học sinh cấp 3. Điều tra 200 học sinh cấp 3 thấy có 45 em thường xuyên đọc báo đó. Với độ tin cậy 95% hãy kiểm định tính chính xác của thông báo trên.
Giải
H0 : p 0, 25
H : p 0, 25
1
f 45
0, 225
Hàm kiểm định
200
0, 225 0, 25 200
0, 251 0, 25
K 0,806
1 0,95 u
2
1,96
Miền bác bỏ giả thuyết là
W, 1,961,96,
K 1,96
Vậy ta không có đủ cơ sở để bác bỏ thông báo đó.
Ví dụ 4.9. Một máy sản xuất tự động, lúc đầu tỷ lệ sản phẩm loại A là 45%. Sau khi áp dụng một phương pháp sản xuất mới, người ta lấy ra 400 sản phẩm để kiểm tra, qua kiểm tra thấy có 215 sản phẩm loại A. Với mức ý nghĩa hãy kết luận xem phương pháp sản xuất mới có thực sự làm tăng tỷ lệ sản phẩm loại A lên hay không?
Giải
H0 : p 0, 45
H : p 0, 45
1
Tỷ lệ sản phẩm loại A của mẫu là: f = 0,5375.
(0,5375 0, 45) 400
0, 45.0,55
Ta có giá trị kiểm định: K 3,5176
Với mức ý nghĩa , tra bảng ta được: u 1,645 .
Miền bác bỏ: W (1,645 ;
)
Ta thấy K W
nên bác bỏ H0 và chấp nhận H1, tức là p > 0,45.
Kết luận: Phương pháp sản suất mới thực sự làm tăng tỷ lệ sản phẩm loại A lên.
4.7. Kiểm định về sự bằng nhau của hai kỳ vọng
Giả sử
X : N ;2 ;Y : N ;2 , nếu muốn so sánh và người ta đưa
ra giả thuyết
1 1 2 2 1 2
H0 : 1 =2
Ta xét hai trường hợp sau:
4.7.1 Bài toán 1: Trường hợp biết
Ta sử dụng hàm kiểm định
VX 2
và VY 2
1
2
K X Y
2
1 2
n1 n2
2
a. Kiểm định hai phía
Ta cần kiểm định giả thuyết:
H0 : 1 =2
H :
1 1 2
Nếu giả thuyết H0 đúng thì U ~ N(0, 1). Nên với mức ý nghĩa , ta xác định
được phân vị
u/2 (tra bảng Laplace) của đại lượng ngẫu nhiên K ~ N(0, 1) sao cho:
P u U u
2 2
Suy ra miền bác bỏ H0 là:
W; u U u ;
b. Kiểm định phía trái
2 2
Ta cần kiểm định giả thuyết
H0 : 1 2
H :
1 1 2
chuẩn
Tương tự như kiểm định hai phía, với mức ý nghĩa cho trước, giá trị phân vị
u/2 được thay bằng phân vị u. Suy ra miền bác bỏ:
c. Kiểm định phía phải
W ;
u
Ta cần kiểm định giả thuyết
H0 : 1 2
H :
1 1 2
chuẩn
Tương tự như kiểm định hai phía, với mức ý nghĩa cho trước, giá trị phân vị
u/2 được thay bằng phân vị u. Suy ra miền bác bỏ:
Wu;
Ví dụ 4.10. Trọng lượng sản phẩm do hai nhà máy sản xuất là các đại lượng ngẫu
nhiên có phân phối chuẩn và có cùng độ lệch tiêu chuẩn là
1kg. Với mức ý nghĩa
0,05 , có thể xem trọng lượng trung bình của sản phẩm do hai nhà máy sản suất là như nhau không? Nếu cân thử 25 sản phẩm của nhà máy A tính được x 50 kg, cân 20 sản phẩm của nhà máy B thì tính được y 50,6 kg.
Giải
Ta kiểm tra giả thuyết
H0 : EX EY
H : EX EY
1
Với mức ý nghĩa
0, 05 thì phân vị chuẩn
u 1, 96.
2
Suy ra miền bác bỏ: W (;1,96) (1,96; )
Giá trị kiểm định:
K 50 50, 6
2.
1 1
Ta thấy K W
25 20
nên bác bỏ giả thuyết H0. Vậy trọng lượng trung bình của sản
phẩm ở 2 nhà máy khác nhau.
4.7.2. Bài toán 2: Trường hợp chưa biết
1
VX 2
và VY 2
Ta chọn thống kê: K
2
X Y
làm tiêu chuẩn kiểm
(n 1)s2 (n 1)s2 1 1
định.
a. Kiểm định hai phía
1 1 2 2
n1 n2 2 n1 n2
H0 : 1 =2
H :
1 1 2
Nếu H0 đúng thì K ~ T(n - 2), với n = n1 + n2.
Với mức ý nghĩa xác định phân vị Student
Suy ra miền bác bỏ H0 được xác định bởi:
t tn2 (1 .
b. Kiểm định phía trái
W ;
tt;
H0 : 1 2
H :
1 1 2
Với mức ý nghĩa , thì phân vị ở quy tắc nêu trên được thay bằng
t2 tn2 (1 2) . Suy ra miền bác bỏ:
b. Kiểm định phía phải
W;
t2.
H0 : 1 2
H :
1 1 2
Với mức ý nghĩa , thì phân vị ở quy tắc nêu trên được thay bằng
t2 tn2 (1 2) . Suy ra miền bác bỏ:
Wt2;
Chú ý: Khi n 30 thống kê K sẽ có phân phối tiệm cận phân phối chuẩn. Bài toán
2
1
kiểm định làm tương tự như trong trường hợp đã biết 2 và 2 nhưng thay các đại
lượng
2 và 2
bởi s2
và s2 .
2
1
2
1
Ví dụ 4.11. Một công ty muốn giảm giá ít nhất để tăng doanh số bán hàng. Để xác định điều đó, ta chọn ngẫu nhiên 15 tuần trước khi giảm giá và 12 tuần sau khi thực hiện một sự giảm giá nhỏ, doanh số trung bình và độ lệch chuẩn tính được lần lượt là: 6598, 6870 và 844, 669 (nghìn đồng). Có thể kết luận một sự giảm giá ít nhất cũng đủ làm tăng doanh số được không?
Giải
Gọi
1 ,2
là doanh số trung bình trước và sau khi giảm giá. Để xét xem phải
chăng doanh số tăng lên sau khi thực hiện giảm giá, ta đặt giả thuyết:
H0 : 1 2
H :
1 1 2
Giả sử phương sai về doanh số ở hai mức là bằng nhau, khi đó ta có:
K 6598 6870
14.(844)2 11.(669)2
1 1
0,91
25 15 12
Miền bác bỏ H0 là:
W;
t2
Với giá trị
t2có bậc tự do 25 luôn thỏa mãn t > t2
do đó K W
nên có thể
chấp nhận H0. Vậy sự giảm giá ít nhất không dẫn đến việc tăng doanh số bán hàng.