Khoảng Tin Cậy Cho Phương Sai Trong Trường Hợp K Ỳ Vọng  Đã Biết

Từ công thức 

s , ta suy ra:

n

u



2

 n

s

u 

2

Vậy độ tin cậy của ước lượng:

(u) 1.

Ví dụ 3.18. Trọng lượng của một hộp sữa do một dây chuyền tự động đóng gói tuân theo luật phân phối chuẩn với độ lệch chuẩn là 10 (gr). Cần phải lấy mẫu kích thước n tối thiểu bằng bao nhiêu để với độ tin cậy 95% sai số của ước lượng không vượt quá 2 (gr).

Giải

Theo bài ra ta có:

 10,0  2, u/2  1,96 , do đó:



2 10 2 

n 

u  1 2 1, 96 

 1 96, 04 1  97



0 2 



Vậy cần chọn tối thiểu 97 hộp sữa.

Ví dụ 3.19. Để nghiên cứu nhu cầu một loại mặt hàng ở một khu vực (đơn vị: kg/tháng), người ta tiến hành khảo sát về nhu cầu mặt hàng này ở 400 hộ gia đình. Kết quả khảo sát cho ở bảng sau:

Nhu cầu

<1	1-2	2-3	3-4	4-5	5-6	6-7	7-8
Số hộ	10	35	86	132	78	31	18	10

Có thể bạn quan tâm!

• Lý thuyết xác suất và thống kê toán - 9
• Lý thuyết xác suất và thống kê toán - 10
• Các Tính Chất Của Ước Lượng Điểm
• Lý thuyết xác suất và thống kê toán - 13
• Bài Toán 1 : Phương Sai Vx = Σ 2 Đã Biết
• Kiểm Định Về Sự Bằng Nhau Của Hai Kỳ Vọng

Xem toàn bộ 168 trang tài liệu này.

Giả sử khu vực này có 4000 hộ.

a) Ước lượng nhu cầu trung bình về mặt hàng này của toàn khu vực trong một năm với độ tin cậy 95%,

b) Khi ước lượng nhu cầu trung bình về mặt hàng này của toàn khu vực trong một năm, nếu ta muốn độ tin cậy đạt được 99% và độ chính xác là 4,8 tấn thì cần khảo sát về nhu cầu này ở bao nhiêu hộ gia đình.

Giải

a) Gọi M là nhu cầu trung bình về mặt hàng này của toàn khu vực trong một năm, là nhu cầu trung bình về mặt hàng này của một hộ trong một tháng.

Trước hết ta tìm khoảng tin cậy của :

400

Độ chính xác của ước lượng là: x  3,62kg, s  1, 44

n

s

Khoảng tin cậy cho là:

u 

2

1, 44 1,96  0,14

(3,62  0,14;3,62  0,14)  (3, 48;3,76) (kg)

Suy ra khoảng tin cậy cho M là:

(3,48. 4000. 12; 3,76. 4000. 12) = (167040; 180480) (kg)

b) Ta cần xác định kích thước mẫu n với độ tin cậy 99% và độ chính xác 4,8 tấn (4,8 tấn = 4800kg). Chú ý là độ chính xác này tương ứng với khoảng tin cậy M, do đó ta suy ra độ chính xác ứng với là:

0 

4800

12.4000

 0,1

Gọi m là số hộ gia đình cần khảo sát về nhu cầu của mặt hàng này, khi đó

 s 2  2,58.1, 44 2

n1 

u

0,1

 1380, 27

0 

Vậy số hộ cần khảo sát là 1381 hộ.

Ví dụ 3.20. Sai số đo của một loại dụng cụ đo có phân phối chuẩn với độ lệch bằng

20. Cần phải tiến hành bao nhiêu phép đo độc lập để sai số phạm phải không vượt quá 5 với độ tin cậy 90%?

Giải

Đây là bài toán tìm kích thước mẫu định lượng biết độ tin cậy 1- α = 0,9 và độ chính xác  = 5, độ lệch chuẩn của tổng thể  = 20 đã biết.

n

Theo công thức tính độ chính xác, ta có:  = uα/2 σ .

u

2 

Suy ra: n =

/ 2

 + 1





Tra bảng hàm số Laplace, ta thấy  (1,65) = 1 - 0,1

2

= 0,95

uα/2 = 1,65

1,65.202 

Vậy: n =







5 

+ 1 = 44.

Cần tiến hành 44 phép đo độc lập.

3.3.3. Khoảng tin cậy cho phương sai

Giả sử biến ngẫu nhiên X :

N ;2 

và tham số VX 2

chưa biết, ngoài ra ta

biết được mẫu quan sát của X là (x1 , x2 , . . . , xn) . Bài toán đặt ra là: tìm khoảng tin

cậy cho VX 2

với độ tin cậy 1

cho trước. Ta xét 2 trường hợp sau:

a. Bài toán : Kỳ vọng đã biết

1

Giả sử (X1, X2, ..., Xn) là mẫu tổng quát từ X ~ Khi đó ta có:

N , 2 , với đã biết.

n

2 

2

(Xi

)2 ~ 2 (n)

i1

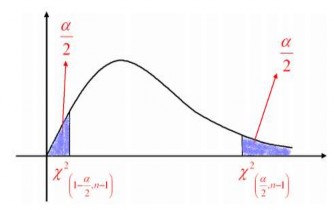
Hình 3.3: Khoảng tin cậy cho phương sai trong trường hợp kỳ vọng đã biết

n 2

n 2

Với độ tin cậy 1 cho trước ta tìm được các giá trị phân vị sao cho:

2 (1),

2 ( )

1

P 2  n

2 2 

n(12) 2(Xi)

n ( 2 )12 2  1

hay

i1

n 2 n



2 

(Xi) (Xi) 

P i12 i1 1

2 ( ) 2 (1)

n 2



n 2 



Từ đó ta đưa ta quy tắc tìm khoảng ước lượng hai phía cho phương sai trong trường hợp đã biết kỳ vọng :

k

- Từ mẫu cụ thể (x1, x2, ... , xn) ta tính giá trị: ni(xi)

2

i1

- Với độ tin cậy 1 ta tìm các giá trị phân vị: 2 (1),2 ( )

n 2 n 2

Khi đó: khoảng tin cậy hai phía cho phương sai 2 là:

k 2 k 2 

ni(xi) ni(xi) 

i1;i1

2 ( ) 2 (1) 

n 2 n 2 



Chú ý:

n 2

- Các giá trị phân vị 2 ( )

và 2 (1)

của ĐLNN 2 ~ 2 (n)

thỏa mãn

n 2

điều kiện sau:

P22( ) 1 ; P22(1)

n 2

n 2 2 n 22

n 2

- Để tìm

2 ( )

và 2 (1)

ta có thể tra bảng phân phối khi bình phương

n bậc tự do (bảng 4) hoặc bằng Excel (phụ lục).

Xây dựng tương tự như khoảng tin cậy hai phía, ta thu được các khoảng tin cậy phải và trái như sau:



k 2 

ni(xi)

* Khoảng tin cậy phải: i1



; 

n 2

2 ( ) 









k

2

ni(xi) 

* Khoảng tin cậy trái:  ;

i1

n 2

2 (1 ) 





b. Bài toán 2: Kỳ vọng EX = chưa biết

Xây dựng khoảng tin cậy dựa trên các thống kê sau:

2  (n  1)s2

2

~ 2

(n  1)

2

có phân phối khi bình phương (n-1) bậc tự do.

Bằng cách xây dựng như trên, tra có quy tắc tìm khoảng ước lượng hai phía cho phương sai trong trường hợp chưa biết kỳ vọng :

- Từ mẫu cụ thể (x1, x2, ... , xn) ta tính giá trị: (n 1)s2

- Với độ tin cậy 1 ta tìm các giá trị phân vị: 2 (1),2 ()

n1 2 n1 2

Khi đó: khoảng tin cậy hai phía cho phương sai 2

của tổng thể là

 (n 1)s2 (n 1)s2 

2

;

( )

2 (1) 

n1 2 n1 2 

Xây dựng tương tự như khoảng tin cậy hai phía, ta thu được các khoảng tin cậy phải và trái như sau:

 (n 1)s2 

* Khoảng tin cậy phải: 2

( )

; 

n1 2





(n 1)s2 

* Khoảng tin cậy trái:  ;

2 (1) 

n1 2 

Ví dụ 3.21. Theo dòi số hàng bán được mỗi ngày ở một trung tâm thương mại, ta được kết quả ghi ở bảng sau:

Số hàng bán được (kg/ngày)	Số ngày
1900-1950	2
1950-2000	10
2000-2050	8
2050-2100	5

Hãy ước lượng phương sai của lượng hàng bán được mỗi ngày với độ tin cậy 95%. Biết lượng hàng hóa bán được mỗi ngày tuân theo luật phân phối chuẩn?

Giải

Ta lập bảng để tính s2 và thu được: s2 = 2058,333 Với độ tin vậy 95% thì:

2 () 2 (0,025)  39,364

n1 2 24

2 (1) 2 (0,975)  12, 401

n1 2 24

Vậy khoảng tin cậy hai phía:

 24.2058,333 ; 24.2058,333 

 39,364 12, 401 

hay



1254,954 ; 3983,5497

Ví dụ 3.22. Cho khối lượng một loại sản phẩm tuân theo luật phân phối chuẩn. Cân thử từng sản phẩm của một mẫu ngẫu nhiên gồm 25 sản phẩm, kết quả thu được như sau:

Khối lượng (gam)

29,3	29,7	30	30,5	30,7
Số sản phẩm	4	5	8	5	3

Với độ tin cậy 95%, hãy tìm khoảng tin cậy cho phương sai của khối lượng sản phẩm trong 2 trường hợp:

a) Biết EX = 30;

b) Không biết EX.

Giải

k

Từ mẫu cụ thể (x1, x2, ... , xn) ta tính giá trị: ni(xi

 30)2  5.13

i1

Với độ tin cậy 95% ta tìm các giá trị phân vị:

2 () 2 (0,025)  40,647

n 2 25

2 (1) 2 (0,975)  13,12

n 2 25

Khoảng tin cậy hai phía cho phương sai 2

của tổng thể



 5,13 ; 5,13 

 40, 647 13,12 

hay 0,1262 ; 0,391

b) Sử dụng máy tính điện tử tính được: s = 0,4621688, s2=0,2136 Với độ tin vậy 95% thì:

2 () 2 (0,025)  39,364

n1 2 24

2 (1) 2 (0,975)  12, 401

n1 2 24

Vậy khoảng tin cậy hai phía:

 24.0, 2136 ; 24.0, 2136 

 39,364 12, 401 

hay



0,1302 ; 0,4134

Ví dụ 3.23. Theo dòi số hàng bán được trong một ngày ở một cửa hàng, ta được kết quả ghi ở bảng sau:

Số hàng bán được (kg)

Số ngày
1900 – 1950	2
1950 – 2000	10
2000 – 2050	8
2050 – 2100	5

95%.

Giải

Hãy ước lượng phương sai của lượng hàng bán được mỗi ngày với độ tin cậy

Từ mẫu định lượng đã cho, ta tính được n = 25, s2 = 2058,3333.

Tra bảng phân phối “khi bình phương” dòng 24, cột 0,025 và cột 0,975 ta được:

2 () 2

(0,025)  39,364

1 n1 2 24

2 (1) 2

(0,975)  12, 401

2 n1 2

(n 1)s2

24

(n 1)s2

Suy ra:

1

= 1254,7944 ;

= 3983,5497.

χ 2

Vậy khoảng ước lượng của phương sai của tổng thể là:

1356,5838 < 2 < 3567,3021.

3.3.4. Khoảng tin cậy cho tỷ lệ

Ước lượng khoảng đối với tỷ lệ (xác suất) nào đó là bài toán thường gặp trong nhiều lĩnh vực và cuộc sống. Xác suất p chính là tham số của phân phối nhị thức.

Giả sử tổng thể có n phần tử, trong đó có m phần tử mang dấu hiệu nghiên

cứu (phần tử có tính chất A). Khi đó:

p m

n

là tỷ lệ phần tử có tính chất A của tổng

thể hay xác suất để lấy ngẫu nhiên 1 phần tử thì được phần tử mang dấu hiệu nghiên

lệ p=?

cứu. Nhưng thực tế n và m rất khó xác định nên tỷ lệ p. Ta phải ước lượng tỷ

Từ tổng thể đó ta lập một mẫu ngẫu nhiên có kích thước n, trong đó có m phần

tử mang dấu hiệu nghiên cứu.

Với độ tin cậy 1 cho trước, tìm khoảng tin cậy (p1 , p2) sao cho:

(F  p) n

p(1 p)

Pp1 p  p2 1

Thông thường, thì thống kê

~ N(0;1)

do đó:



P u

(F  p



)n

p(1 P)

 u  1

Hay



2 2 

p(1 p)

n

p(1 p)

n



P F  u 

 p  F  u 

 1

2 2 

Đặt f =

m được gọi là tần suất mẫu xuất hiện dấu hiệu cần nghiên cứu.

n

a. Bài toán 1: n lớn và p không quá gần 0, 1

Khi kích thước mẫu n khá lớn thì ta có thể xấp xỉ f  p . Quy tắc: tìm khoảng ước lượng đối xứng cho tỷ lệ của tổng thể

- Từ mẫu cụ thể tính f = m .

n

- Tính giá trị phân vị u rồi tính độ chính xác của ước lượng:

f (1 f )

n

2

 u



2

Khi đó: với xác suất 1 –  cho trước, khoảng tin cậy đối xứng cho tỷ lệ p là:

f  f 

Hoàn toàn tương tự, ta có thể đưa ra khoảng tin cậy trái và khoảng tin cậy phải như sau:

* Khoảng tin cậy phải: f  ; 

* Khoảng tin cậy trái:  ;f 

f (1 f )

n

trong đó, độ chính xác của ước lượng:  u



Chú ý:

- Ước lượng cho xác suất (hoặc tỷ lệ nào đó) là bài toán rất thường gặp trong thực tế, đặc biệt là trong thực nghiệm.

- Quan hệ:

2 f (1 f ) u2 , với là độ chính xác của ước lượng.

n



2

Ví dụ 3.24. Kiểm tra ngẫu nhiên 600 sản phẩm của một máy dập thấy có 24 phế phẩm. Với độ tin cậy 95% hãy ước lượng tỷ lệ phế phẩm tối đa của máy đó.

Giải

Gọi p là tỷ lệ phế phẩm của máy dập.

n  600 (khá lớn)

Tỷ lệ phế phẩm mẫu: f 

24

600

 0, 04

Giá trị phân vị:

u  1,96

2

0, 04.0,96

600

Độ chính xác của ước lượng:  1,96  0, 01568

Khoảng tin cậy cho tỷ lệ phế phẩm tối đa là ;0, 05568

Ví dụ 3.25. Trước ngày bầu cử tổng thống, người ta phỏng vấn ngẫu nhiên 1800 cử tri thì thấy có 1180 người ủng hộ ứng cử viên A. Với độ tin cậy 95%, hãy ước lượng tỷ lệ cử tri ủng hộ ứng cử viên A bằng khoảng tin cậy đối xứng?

Giải

Gọi p là tỷ lệ các phần tử ủng hộ ứng cử viên A

Ta có mẫu gồm 1800 phần tử, trong đó có 1180 phần tử ủng hộ ứng cử viên A nên tỉ lệ mẫu là:

f = 1180 = 0,6556.

1800

Tra bảng hàm số Laplace ta thấy:

(1,96) = 1 - 0, 05  0,975

2

nên uα/2 = 1,96

Độ chính xác của ước lượng là

0,6556(10,6556)

1800

 = 1,96

= 0,022.

Do đó tỉ lệ tổng thể ủng hộ ứng cử viên A là:

p = 0,6556  0,022 hay 0,6336  p  0,6776.

b. Bài toán 2: n lớn và p xấp xỉ 0 hoặc 1

Phân phối của p xấp xỉ phân phối Poisson với tham số

np

. Trên cơ sở đó ta

lập được các giá trị trong bảng V, tương ứng với giá trị m, tra bảng tìm được với độ tin cậy 95% do đó khoảng tin cậy 95% của p là p1; p2 

np1, np2

Ví dụ 3.26. Kiểm tra 1000 người có 15 người nghi ngờ mắc bệnh gan. Xét nghiệm tiếp có 3 người mắc bệnh gan. Chỉ ra ước lượng khoảng cho tỷ lệ người mắc bệnh gan?