Kiểm Định Sự Bằng Nhau Của 2 Tỷ Lệ

Ví dụ 4.12. Người ta nghiên cứu năng suất lúa ở hai vùng có hai chế độ canh tác khác nhau. Vùng thứ nhất có 40 thửa ruộng được chọn với năng suất bình quân x  24,6

tạ/ha tạ/ha

s2  0, 24 ; ở vùng thứ hai có 70 thửa ruộng với năng suất bình quân y  25,8

1

2

s2  0,16 . Với , hỏi có sự khác nhau đáng kể giữa năng suất trung bình

của hai vùng trên?

Giải

Gọi 1 ,2

tương ứng là năng suất trung bình của vùng thứ nhất và vùng thứ hai

(n1 > 30, n2 > 30). Ta cần kiểm định giả thuyết sau:

H0 : 1 2

H : 

Ta có:

K  x  y

1 1 2

s

2

1 2

s

2

n1 n2



0, 240,16

40 70

 24, 6  25,8

13,19

Với  tra bảng ta được

u  1,96 .

2

Miền bác bỏ giả thuyết H0: W ( ;

1,96)  (1,96 ;

) .

Do K  Wnên bác bỏ H0.nên năng suất lúa ở hai vùng khác nhau.

4.8. Kiểm định sự bằng nhau của 2 tỷ lệ

Với mức ý nghĩa  cho trước, hãy kiểm định giả thuyết

H0 : p1  p2

f1(1 f1)  f2(1  f2)

n1

n2

Ta chọn thống kê K 

f1  f2

làm tiêu chuẩn kiểm định.

Trong đó

f m1 , f

1 n 2

 m2

n

là tần suất mẫu tương ứng với 2 mẫu

1 2

1 2

x1, x2 ,..., xn ; y1, y2 ,..., yn .

Ta xét các loại bài toán kiểm định sau:

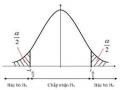
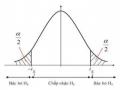
4.8.1. Kiểm định hai phía

H0 : p1  p2

H : p  p

1 1 2

Nếu H0 đúng thì K ~ N(0, 1). Do đó với mức ý nghĩa  , ta xác định được phân

vị chuẩn

u sao cho

2

P{ K

 u }  .

2

Miền bác bỏ giả thuyết H0:

W ( ;

 u )  (u ;

2 2

)

4.8.2. Kiểm định phía trái

H0 : p1  p2

H : p  p

1 1 2

Với mức ý nghĩa  , thì phân vị

u ở quy tắc kiểm định hai phía được thay

2

bằng u.Miền bác bỏ giả thuyết H0: W ( ;

4.8.3. Kiểm định phía phải

 u) .

H0 : p1  p2

H : p  p



Với mức ý nghĩa  , thì phân vị

1 1 2

u ở quy tắc kiểm định hai phía được thay

2

bằng u. Miền bác bỏ giả thuyết H0: W (u;

) .

Ví dụ 4.13. Kiểm tra chất lượng của 2 lô sản phẩm, người ta thấy trong lô thứ nhất gồm 500 sản phẩm thì có 50 phế phẩm; trong lô thứ hai gồm 400 sản phẩm thì thấy có

60 phế phẩm. Với mức ý nghĩa như nhau được không?

Giải

 0, 05

có thể nói chất lượng của 2 lô sản phẩm là

H0 : p1  p2

H : p  p

f1 

50

500

 0,1; f2

 60

400

1 1 2

 0,15

Suy ra K 2, 276

 0, 05

nên u 1, 96

2

Miền bác bỏ: W ( ;

1,96)  (1,96 ;

)

K  1,96 .

Vậy chất lượng của 2 lô sản phẩm khác nhau.

Ví dụ 4.14. Kiểm tra 120 sinh viên của trương A thấy có 80 sinh viên có kết quả học tập đạt loại khá, 150 sinh viên của trường B thấy có 90 sinh viên đạt loại khá. Hỏi tỷ lệ sinh viên khá của trường A có lớn hơn trường B không, biết mức ý nghĩa  .

Giải

Gọi p1, p2 tương ứng là tỷ lệ sinh viên đạt loại khá của hai trường A và B. Khi đó ta cần kiểm định giả thuyết:

H0 : p1  p2

H : p  p

1 1 2

Ta có: f1

 80

120

 0,666 ; f2

 90

150

 0,6

nên

f1(1 f1)  f2 (1 f2 )

n1

n2

K  f1  f2

 0, 666  0, 6

0, 666(1 0, 666)0, 6(1 0, 6)

120 150

 1,123

Miền bác bỏ: W (1,645; )

Ta thấy K  Wthì chấp nhận H0 , vậy có thể coi tỷ lệ sinh viên đạt loại khá của

hai trường A và B như nhau.

HƯỚNG DẪN TỰ HỌC CHƯƠNG 4

Trong chương này ta xét một bài toán với các quy ước sau:

- Mỗi bài toán chỉ có hai tình huống được đưa ra để bàn bạc, phân tích.

- Cuối cùng ta phải chọn lấy một và bác bỏ một trong hai tình huống trên.

Dĩ nhiên, ta sẽ chọn tình huống nào để sai ít hơn. Bài toán luôn có nghiệm vì giữa hai tình huống luôn có sự so sánh về khả năng đúng, sai.

Ý tưởng cơ bản để giải bài toán này đó là chia miền giá trị có thể của mẫu ngẫu nhiên thành hai phần bù nhau: miền chấp nhận và miền bác bỏ.

Giả thuyết đưa ra kiểm định được ký hiệu là

H0 , đó là giả thuyết mà ta nghi

ngờ, muốn bác bỏ hoặc giả thuyết ta muốn bảo vệ. Đối thuyết

H1 được chấp nhận khi

H0

H0 .

bị bác bỏ. Cần chú ý: đối thuyết

H1 không nhất thiết là phủ định của giả thuyết

Ví dụ:

Giả thuyết

H0 : nhu cầu thị trường về một loại hàng hóa là

 1000

đơn

vị/tháng.

Nếu ta nghi ngờ nhu cầu này không đúng thì đối thuyết

H1 :

 1000

Nhưng do chính sách khuyến mại tốt, người ta nghĩ rằng nhu cầu về mặt hàng

này tăng lên, khi đó đối thuyết

H1 :  1000 .

Quy tắc kiểm định dựa trên hai nguyên lý sau:

- Nguyên lý xác suất nhỏ: Nếu một biến cố có xác suất rất nhỏ thì trong một hay vài phép thử biến cố đó coi như không xảy ra.

- Phương pháp phản chứng: Để bác bỏ A, ta giả sử A đúng dẫn đến một điều vô

lý.

Quy trình giải bài toán kiểm định giả thuyết thống kê gồm các bước sau:

Bước 1: Phát biểu giả thuyết

H0 , đối thuyết

H1 ;

Bước 2: Từ tổng thể, lập mẫu ngẫu nhiên cỡ n

Bước 3: Từ mẫu cụ thể, tính giá trị hàm kiểm định K

Bước 4: Với mức ý nghĩa , xác định miền bác bỏ H0 là w

Bước 5: So sánh giá trị của hàm K và miền bác bỏ wrồi kết luận.

CÂU HỎI ÔN TẬP CHƯƠNG 4

4.1. Giả thuyết thống kê là giả thuyết do nhà thống kê đặt ra cho mẫu ngẫu nhiên.

a) Đúng b) Sai

4.2. Bác bỏ giả thuyết là chấp nhận đối thuyết và ngược lại, do đó đối thuyết là phủ định của giả thuyết.

a) Đúng b) Sai

4.3. Quy tắc kiểm định dựa trên nguyên lý xác suất nhỏ và phương pháp phản chứng.

a) Đúng b) Sai

4.4. Sai lầm loại I là sai lầm gặp phải khi thực tế giả thuyết đúng nhưng ta bác bỏ.

a) Đúng b) Sai

4.5. Sai lầm loại II luôn lớn hơn sai lầm loại I.

a) Đúng b) Sai

4.6. Kiểm định hai phía là kiểm định với những tham số có thể nhận giá trị âm hoặc dương bất kỳ.

a) Đúng b) Sai

4.7. Kiểm định một phía khi tham số cần kiểm định chỉ nhận giá trị âm hoặc dương.

a) Đúng b) Sai

4.8. Miền bác bỏ là miền có xác suất rất bé nên ta có thể bỏ qua trong mọi phép kiểm định.

a) Đúng b) Sai

BÀI TẬP CHƯƠNG 4

4.1. Một ông chủ cửa hàng sản xuất bồn nước cho biết dung tích trung bình của bồn là

55 lít, độ lệch tiêu chuẩn là 6 lít. Với  0, 001 hãy kiểm tra ý kiến của ông chủ cửa

hàng biết khi kiểm tra 36 bồn nước thấy dung tích trung bình chỉ có 49 lít.

4.2. Một công ty dự định mở một siêu thị ở thị xã A. Để đánh giá khả năng mua hàng của nhân dân ở đó, người ta điều tra thu nhập bình quân hàng tháng của 100 hộ dân được kết quả sau:

Thu nhập bình quân

(Nghìn đồng/người/tháng)

500	550	600	650	700
Số hộ	8	15	38	22	17

Có thể bạn quan tâm!

• Lý thuyết xác suất và thống kê toán - 13
• Bài Toán 1 : Phương Sai Vx = Σ 2 Đã Biết
• Kiểm Định Về Sự Bằng Nhau Của Hai Kỳ Vọng
• Không Thể Kết Luận Học Sinh Nội Thàn Có Thể Lực Tốt Hơn
• Công Thức Ước Lượng Hệ Số Của Đường Hồi Quy Tuyến Tính
• Lý thuyết xác suất và thống kê toán - 19

Xem toàn bộ 168 trang tài liệu này.

Hoạt động của siêu thị có hiệu quả nếu thu nhập bình quân tối thiểu là 650 nghìn đồng, vậy công ty có nên mở siêu thị tại thị xã A không, biết độ tin cậy là 90%.

Lượng tiêu dùng	100-120	120-140	140-160	160-180	180-200
Số hộ	14	25	30	20	11

4.3. Trước đây, định mức tiêu dùng điện là 140 KW cho 1 hộ gia đình / tháng. Do đời sống nâng cao, điều tra 100 hộ được kết quả sau:

Với mức ý nghĩa hay không?

 5%

, theo anh chị có cần nâng định mức tiêu dùng điện

4.4. Gieo 300 hạt giống ta thấy có 261 hạt nảy mầm. Người ta nói rằng tỷ lệ nảy mầm của hạt giống là 90% với mức 0,05 có đúng không?

4.5. Trong một lô hạt giống, người ta nói rằng tỷ lệ hạt giống lép là 0,02. Ta chọn ngẫu nhiên có hoàn lại 480 hạt thấy có 42 hạt lép. Xét xem tỷ lệ hạt lép người ta thông báo với mức 0,05 có đúng không?

4.6. Giả sử sản phẩm của một công ty sản xuất xe ô tô đã chiếm được 42% thị trường. Hiện tại trước sự cạnh tranh của các đối thủ và những điều kiện của môi trường kinh doanh, ban lãnh đạo muốn kiểm tra lại xem thị trường của công ty có còn đạt 42% nữa không. Chọn ngẫu nhiên 550 xe ô tô trên đường kết quả cho thấy có 219 xe có sử dụng xe của công ty. Có thể kết luận gì, ở mức ý nghĩa 1%.

4.7. Theo quy định, một lô hàng được xem là đạt tiêu chuẩn nếu tỉ lệ phế phẩm của lô hàng không quá 5%. Tiến hành kiểm tra 100 sản phẩm của lô hàng thì thấy có 8 phế phẩm. Với mức ý nghĩa 5%, hãy cho kết luận về lô hàng đó.

4.8. Khi điều trị bằng thuốc A, tỉ lệ bệnh nhân khỏi bệnh là 80%. Đổi sang thuốc B để điều trị cho 110 người thì thấy có 920 người khỏi bệnh. Với mức ý nghĩa  = 0,02 có thể cho rằng thuốc B hiệu quả hơn thuốc A hay không ?

4.9. Một máy sản xuất tự động có tỉ lệ sản phẩm không đạt tiêu chuẩn là 20%. Sau khi áp dụng phương pháp sản xuất mới, người ta lấy 40 thùng hàng, mỗi thùng có 10 sản phẩm để kiểm tra. Kết quả cho trong bảng sau:

Số sản phẩm

không đạt tiêu chuẩn

1	2	3	4	5	6	7	8	9	10
Số thùng hàng	2	0	4	6	8	10	4	5	1	0

Với mức ý nghĩa  = 0,05, hãy đánh giá hiệu quả của phương pháp sản xuất mới này.

4.10. Theo dòi số tai nạn lao động của hai xí nghiệp trong một thời gian ta có số liệu sau. Xí nghiệp thứ nhất: 20 tai nạn/400 công nhân. Xí nghiệp thứ hai: 28 tai nạn/500 công nhân. Hỏi có sự khác nhau đáng kể về chất lượng công tác phòng

hộ lao động ở hai xí nghiệp đó với  = 2% ?

4.11. Năng suất lúa trung bình ở vụ trước là 4,5 tấn/ha. Vụ lúa năm nay người ta áp dụng biện pháp kĩ thuật mới cho toàn bộ diện tích trồng lúa trong vùng. Theo dòi 100 ha ta có bảng năng suất lúa sau đây:

Năng suất

(tạ/ha)

Diện tích (ha)	Năng suất	Diện tích
30 – 35	7	50 – 55	20
35 – 40	12	55 – 60	8
40 – 45	18	60 – 65	5
45 – 50	27	65 – 70	3

Với  = 0,01 hãy kết luận về biện pháp kĩ thuật mới.

4.12. Để nghiên cứu nhu cầu một loại hàng, người ta khảo sát nhu cầu của mặt hàng này ở một số hộ gia đình. Kết quả cho ở bảng sau.

Nhu cầu

(kg/tháng)

Số hộ gia đình	Nhu cầu	Số hộ gia đình
< 1	10	4 – 5	78
1 – 2	35	5 – 6	31
2 – 3	86	6 – 7	18
3 – 4	132	7 – 8	10

Giả sử khu vực đó có 4000 hộ gia đình. Nếu cho rằng nhu cầu trung bình về mặt hàng này của toàn khu vực là 168 tấn trong một năm thì có chấp nhận được không với mức ý nghĩa 1% ?

4.13. Tỷ lệ phế phẩm ở một nhà máy cần đạt là 10%. Sau khi cải tiến, kiểm tra 400 sản phẩm thì thấy có 32 phế phẩm với độ tin cậy 99%. Hãy xét xem việc cải tiến kỹ thuật có kết quả hay không?

4.14. Theo báo cáo, tỉ lệ hàng phế phẩm trong kho là 10%. Kiểm tra ngẫu nhiên 100 sản phẩm thấy có 8 phế phẩm. Hỏi báo cáo trên có đáng tin ở mức ý nghĩa 5% không?

4.15. Trước đây tỉ lệ phế phẩm của một nhà máy là 5%. Năm nay người ta áp dụng một biện pháp kĩ thuật mới để sản xuất. Sau một thời gian, kiểm tra 800 sản phẩm thì thấy có 24 phế phẩm. Với mức ý nghĩa 1%, hãy đánh giá hiệu quả của biện pháp kĩ thuật đó.

4.16. Độ bền của một loại dây thép sản xuất theo công nghệ cũ là 150. Sau khi cải tiến kĩ thuật người ta lấy 100 sợi dây thép để thử thì thấy độ bền trung bình là 185 và S =

25. Với  = 0,03 hãy kết luận hiệu quả của việc cải tiến kĩ thuật.

4.17. Kiểm tra các sản phẩm do hai phân xưởng sản xuất, ta có các số liệu sau đây.

Phân

xưởng

Số sản phẩm được kiểm tra	Khối lượng trung bình (kg)	Phương sai mẫu hiệu chỉnh	Số phế phẩm
1 2	900 800	50,2 50,1	0,16 0,20	18 16

a) Với mức ý nghĩa 0,05 có thể coi khối lượng trung bình của các sản phẩm do hai phân xưởng sản xuất là như nhau được không ?

b) Với mức ý nghĩa 0,01 có thể coi tỉ lệ phế phẩm của hai phân xưởng cũng như nhau hay không ?

4.18. Trước đây định mức tiêu hao nhiên liệu cho một loại động cơ trong một ca sản xuất là 14 lít. Do tình hình thay đổi, người ta theo dòi 100 động cơ và thu được các số liệu sau:

Lượng tiêu hao (lít)

10-12	12-14	14-16	16-18	18-20
Số động cơ	13	25	30	20	12

a) Giả thiết lượng tiêu hao nhiên liệu tuân theo luật phân phối chuẩn. Theo anh (chị) có cần thay đổi định mức hay không ? Hãy kết luận với mức ý nghĩa 5%,

b) Động cơ được coi là hoạt động bình thường nếu mức tiêu hao nhiên liệu trong một ca không vượt quá 18 lít. Hãy ước lượng tỷ lệ động cơ hoạt động bình thường tối thiểu trên cơ sở số liệu nói trên với độ tin cậy 95%.

4.19. Điều tra thu nhập hàng năm của 100 công nhân tại xí nghiệp A thu được các số liệu sau:

Thu nhập (triệu đồng/năm)

5,5	5,8	6,0	6,2	6,5
Số công nhân	10	20	35	25	10

Giả thiết thu nhập hàng năm của công nhân có phân phối chuẩn