Hóa học đại cương

1.1.2. Kích thước, khối lượng của nguyên tử

Ngày nay, khoa học có thể xác định được kích thước, khối lượng của nguyên tử và các thành phần cấu tạo nguyên tử.

Kích thước: Nếu hình dung nguyên tử như một khối cầu thì nó có đường kính

-10 0 0

khoảng 10 m hay 1 . Nguyên tử nhỏ nhất là hiđro có bán kính khoảng 0,53 

(1 A =10

-10m).

Đường kính của hạt nhân nguyên tử còn nhỏ hơn, vào khoảng 104 

Đường kính của electron và proton lại còn nhỏ hơn nhiều: khoảng 107 

Khối lượng: Khối lượng một nguyên tử vào khoảng 10-26kg. Nguyên tử nhẹ nhất là hiđro có khối lượng là 1,67.1027 kg

1.2. Cấu tạo nguyên tử

1.2.1. Cấu tạo nguyên tử theo quan điểm của cơ học cổ điển

a. Thuyết Ruzơpho (Rutherford) 1911

Ruzơpho cho rằng: Các electron quay xung quanh hạt nhân giống như các hành tinh quay xung quanh mặt trời.

Theo thuyết điện động lực học, hạt mang điện như electron khi chuyển động tròn sẽ phát ra năng lượng dưới dạng bức xạ. Như thế, electron liên tục mất năng lượng và cuối cùng rơi vào hạt nhân do đó nguyên tử không tồn tại. Mặt khác, theo thuyết Ruzơpho quang phổ phát xạ của nguyên tử phải là quang phổ liên tục, nhưng thực tế cho thấy rằng quang phổ phát xạ của nguyên tử là quang phổ vạch.

b. Thuyết Bo (Bohr) 1913

Thuyết Bo gồm ba định đề:

i. Electron chuyển động quanh hạt nhân trên những quỹ đạo tròn đồng tâm, bán kính tỉ lệ với nhau theo bình phương của những số nguyên

r1: r2: r3…….rn = 12: 22: 32…….n2 hay: rn = r1n2

n là số lượng tử chính

- Khi chuyển động trên quỹ đạo, electron không phát hay thu năng lượng do đó bán kính không thay đổi.

Sự thu hoặc phát năng lượng chỉ xảy ra khi electron chuyển động từ quỹ đạo này đến quỹ đạo khác.

- Khi electron chuyển động từ quỹ đạo này đến quỹ đạo khác, nó sẽ thu hoặc phát một lượng tử năng lượng. Năng lượng đó có thể thể hiện dưới dạng bức xạ điện

tử có tần số (nuy),

ε = hν = hc .

Thuyết Bo đã giải thích thành công nguyên nhân sự phát xạ, tính gián đoạn quang phổ phát xạ của nguyên tử hiđro.

Khi phóng điện qua hiđro, thì electron ở quỹ đạo K (n = 1) trong các nguyên tử hiđro chuyển đến mức năng lượng cao hơn (n = 2,3,4…..). Các trạng thái mới này của nguyên tử hiđro được gọi là trạng thái kích thích. Ở trạng thái kích thích, các electron luôn có xu hướng chuyển về mức năng lượng thấp hơn (nhảy về quỹ đạo gần hạt nhân hơn). Trong quá trình nhảy về, sẽ có sự phát năng lượng từng lượng tử, dưới dạng các bức xạ ánh sáng có tần số .

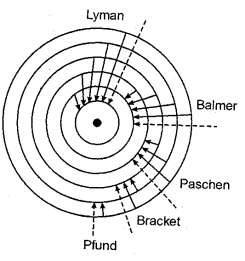
Nếu nđ  2, nc = 1 ta được các vạch trong dãy Lyman

Nếu nđ  3, nc = 2 ta được các vạch trong dãy Balmer

Nếu nđ  4, nc = 3 ta được các vạch trong dãy Paschen

Nếu nđ  5, nc = 4 ta được các vạch trong dãy Bracket

Nếu nđ  6, nc = 5 ta được các

vạch trong dãy Pfund Hình 1.1. Sự xuất hiện các dãy phổ Của nguyên tử hiđro theo thuyết Bo

Vì nđ, nc có những giá trị gián đoạn nên ở hay ν cũng phải có những giá trị gián đoạn. Do đó quang phổ phải là quang phổ vạch (hình 1.1).

Thuyết Bo đã thành công trong việc giải thích quang phổ hiđro. Các phép tính về bước sóng, độ dài sóng của các vạch quang phổ...trong nguyên tử phù hợp với thực nghiệm.

c. Thuyết Xomophen (Sommfen)

Theo Xomophen mỗi quỹ đạo Bo thực ra là một lớp quỹ đạo, trong đó có cả quỹ đạo tròn và quỹ đạo elip. Xomophen cũng đưa ra thêm số lượng tử phụ l để mô tả trạng thái năng lượng của electron trong nguyên tử.

Thuyết Bo-Xomophen không giải thích được thật chi tiết quang phổ của các nguyên tử nhiều electron. Bởi vậy mẫu nguyên tử Bo-Xomophen cần được thay thế bằng những quan điểm hiện đại của cơ học lượng tử.

1.2.2. Cấu tạo nguyên tử theo quan điểm hiện đại của cơ học lượng tử

a. Những tiền đề của cơ học lượng tử

 Bản chất sóng hạt của electron

Theo quan điểm của vật lí hiện đại photon vừa có bản chất sóng, nghĩa là có tần số dao động và tốc độ chuyển động c; vừa có bản chất hạt, nghĩa là có khối lượng m và cùng tốc độ chuyển động c. Tính chất nhị nguyên của photon được thể hiện bằng

biểu thức:

λ h.

Trong đó: ở mô tả tính chất sóng, m mô tả tính chất hạt

Năm 1924 Đơ Brơi (L de Broglie) đưa ra giả thuyết là không phải chỉ có photon mới có bản chất sóng mà những hạt vi mô như electron chẳng hạn cũng có tính chất đó. Chuyển động của các hạt vi mô có thể xem là chuyển động sóng, bước sóng của

chuyển động đó tuân theo hệ thức: λ =

h. (1.1)

Ít năm sau quan điểm về bản chất sóng của electron đã được Đavisơn (C.Davison) và Geme (L.Germen) chứng minh bằng thực nghiệm.

 Hệ thức bất định Hayxenbe (W Heisenberg) 1927: Không thể xác định đồng thời chính xác cả vị trí và tốc độ của vi hạt.

Chẳng hạn, một hạt chuyển động theo phương x với độ bất định về toạ độ là x và độ bất định về tốc độ vx thì hệ thức bất định có dạng:

x.vx

h

2m

(1.2)

Trong đó: h là hằng số Plan (Planck); m là khối lượng của vi hạt

Áp dụng hệ thức bất định cho nguyên tử ta thấy electron không thể quay trên quỹ đạo quanh hạt nhân chính xác như Bo. Điều đó có nghĩa là không thể áp dụng cơ học cổ điển của Niutơn cho các vi hạt mà phải xây dựng môn cơ học mới, đó là cơ học lượng tử.

b. Phương trình Srođinhgơ (E.Schrodinger)

Cơ học lượng tử nghiên cứu chuyển động của các hạt vi mô. Cơ sở của cơ học lượng tử là phương trình sóng Srođinhgơ. Dạng tổng quát của phương trình Srođinhgơ như sau: H = E (1.3)

Trong đó H: Toán tử Haminhtơn (Hamilton),

h: Hằng số Plan;

H = -

8π2m

Δ+U ;

2 2

2

:Toán tử Laplac (Laplace),

 2  2

z2 ;

x y

m: Khối lượng electron; U: Thế năng của electron;

E: Năng lượng toàn phần của electron.

90% 10%

Giải phương trình (1.3) sẽ tìm được hàm  của electron và năng lượng của electron tương ứng với nó. Việc giải chính xác phương trình Srođinhgơ chỉ thực hiện được với nguyên tử và ion có một electron. Với các nguyên tử nhiều electron phải dùng phương pháp gần đúng. Kết quả của phương pháp này giải thích thoả mãn các số liệu thực nghiệm.

Khi giải phương trình Srođinhgơ đối với nguyên tử hiđro thu được các kết quả sau:

A. Hàm sóng  phụ thuộc vào ba số nguyên n, l, m (m: số lượng tử từ).

B. Năng lượng của electron biến thiên gián đoạn theo n.

Xác suất tìm thấy electron cực đại ở Hình 1.2. Đám mây electron của

nguên tử hiđro.

khoảng cách đối với hạt nhân bằng 0,53 A . (hình 1.2)

Như thế xác suất có mặt electron xung quang hạt nhân nguyên tử khoảng 90% gọi là mây electron. Mây electron của nguyên tử hiđro là hình cầu bán kính khoảng

0,53 A .

Như vậy, trong cơ học lượng tử không còn tồn tại khái niệm quỹ đạo mà được thay bằng obitan nguyên tử. Một obitan nguyên tử là một hàm  của electron trong nguyên tử.

Vậy, vùng không gian trong đó xác suất tìm thấy electron lớn nhất là obitan nguyên tử.

c. Bốn số lượng tử đặc trưng cho trạng thái của electron trong nguyên tử

Kết quả giải phương trình Srođinhgơ cho thấy hàm sóng  của electron phụ thuộc vào ba số lượng tử n, l, m và được kí hiệu là nlm. Hàm nlm ứng với ba giá trị của n, l, m được gọi là một obitan nguyên tử.

Những kết quả nghiên cứu lí thuyết và thực nghiệm cho thấy việc mô tả một electron trong nguyên tử là không đầy đủ khi chỉ sử dụng ba số lượng tử trên, mà cần phải đưa ra một số lượng tử nữa là số lượng từ spin ms.

 Số lượng tử chính (n)

Các electron của nguyên tử được chia thành từng lớp electron, mỗi lớp được đặc trưng bằng một giá trị của số lượng tử n. Số lượng tử n nhận các giá trị nguyên dương từ 1 trở lên.

Giá trị của n 1 2 3 4 …

Kí hiệu lớp electron K L M N …

Đối với nguyên tử hiđro hoặc ion một electron như He+, Li2+, n đặc trưng cho mức năng lượng của electron trong nguyên tử hay ion được xét và được tính bằng

công thức

E -13,6 Z2 eV . (1.4)

Trong đó, Z là Số proton của nguyên tử được xét.

Đối với nguyên tử nhiều electron, ngoài sự tương tác của các electron với hạt nhân, còn có sự tương tác giữa các electron với nhau, nên năng lượng của electron còn phụ thuộc vào hai số lượng tử, đó là số lượng tử n và số lượng tử l . Vì vậy trong

trường hợp này giá trị của n chỉ đặc trưng cho mức năng lượng trung bình của một lớp.

 Số lượng tử phụ ( l )

Mỗi lớp electron từ n = 2 trở lên gồm nhiều phân lớp. Mỗi phân lớp electron đặc trưng bằng một giá trị của số lượng tử l . Số phân lớp của mỗi lớp bằng giá trị n chỉ lớp đó.

Số lượng tử phụ l nhận các giá trị nguyên dương từ 0 đến (n - 1)

Giá trị của l : 0 1 2 3…(n - 1) Ký hiệu các phân lớp : s p d f…

Để chỉ phân lớp thuộc lớp nào người ta ghi giá trị của n chỉ lớp đó trước ký hiệu phân lớp.

Ví dụ: Lớp K (n = 1) có một phân lớp 1s (số 1 chỉ lớp n = 1, chữ s chỉ phân lớp

l = 0);

Lớp K (n = 2) có hai phân lớp: 2s (n = 2; l = 0) và 2p (n = 2; l = 1);

Lớp M (n = 3) có ba phân lớp:3s (n = 3; l = 0); 3p (n = 3; l = 1) và 3d(n =3; l

= 2);

Lớp N (n = 4) có bốn phân lớp: 4s (n = 4; l = 0); 4p (n = 4; l = 1); 4d (n = 4; l

= 2) và 4f (n = 4; l = 3).

ý nghĩa:

- l đặc trưng cho phân lớp electron;

- l đặc trưng cho phân mức năng lượng của các electron trong lớp eletron khảo sát, trong một lớp electron năng lượng của các electron tăng theo thứ tự ns - np - nd - nf;

- l đặc trưng cho hình dạng obitan (hình 1.3) và mômen động lượng obitan, nghĩa là mỗi giá trị của l , obitan có hình dạng xác định và mômen động lượng obitan có giá trị xác định.

l (l +1)

= 2π

μ : Mômen động lượng obitan, h: Hằng số Plan.

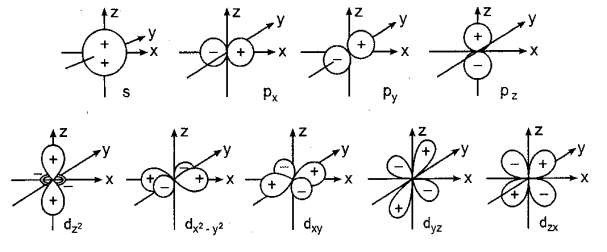
Hình 1.3. Hình dạng và sự định hướng các AO s, p và d

 Số lượng tử từ m

Số lượng tử từ đặc trưng cho sự định hướng của obitan trong không gian (hình 1.3). Nói cách khác nó đặc trưng cho hình chiếu của vectơ momen động lượng obitan

theo phương z: μz =

hm.

2π

z: Hình chiếu của vectơ momen động lượng obitan theo phương z.

Số giá trị của số lượng tử từ phụ thuộc vào số lượng tử phụ l . Ứng với một giá trị của l có ( 2 l + 1) giá trị của m từ - l đến + l (kể cả giá trị 0).

Giá trị của l

Giá trị của m
0	0
1	-1, 0, 1
2	-2, -1, 0, 1, 2
3	-3, -2, -1, 0, 1, 2, 3