Giải pháp điều khiển nghẽn trong mạng OBS bằng phương pháp làm lệch hướng đi - 8

 So sánh các kết quả như hình 4.9:

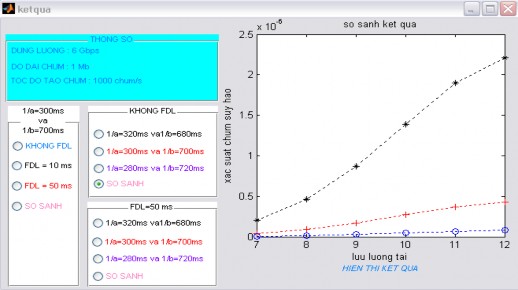
Hình 4.9 Kết quả so sánh

1/

là khoảng thời gian ON tạo chùm và

1/ 

là khoảng thời gian OFF tạo

chùm. Giá trị 1/lớn cũng tương ứng với việc tạo chùm trong hàng đợi lớn. Kết quả

Có thể bạn quan tâm!

• Giải Pháp Điều Khiển Nghẽn Trong Mạng Obs Bằng Phương Pháp Làm Lệch Hướng Đi
• A) Trường Ưu Tiên Trong Gói Điều Khiển
•  N0  1 Thì Tốc Độ Mà Chùm Lấp Đầy Hàng Đợi Là
• Giải pháp điều khiển nghẽn trong mạng OBS bằng phương pháp làm lệch hướng đi - 9
• Giải pháp điều khiển nghẽn trong mạng OBS bằng phương pháp làm lệch hướng đi - 10

Xem toàn bộ 88 trang tài liệu này.

trong hình 4.9 so sánh xác suất chùm suy hao khi thay đổi giá trị

1/

và 1/ . Hình

4.9 cho thấy nếu không sử dụng FDL, khi giảm dần giá trị 1/từ 320ms đến 280ms

thì xác suất chùm suy hao cũng giảm. Điều đó cho thấy quá trình tạo chùm trong hàng đợi nếu với khoảng thời gian ngắn tương ứng với lượng dữ liệu đưa vào mạng ít thì xác suất chùm suy hao sẽ giảm.

Khi sử dụng FDL = 50 ms ta thay đổi khoảng thời gian tạo chùm thì:

 Nếu 1/ 320ms

và 1/  680 ms

thì kết quả như hình 4.10:

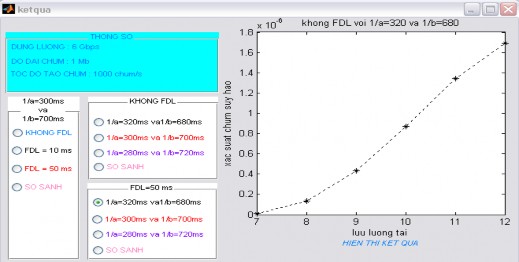
Hình 4.10 Kết quả khi 1/ 320ms và 1/  680 ms

 Nếu 1/ 300ms và 1/  700 ms thì kết quả như hình 4.11:

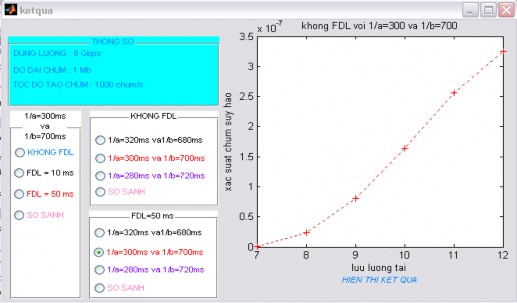
Hình 4.11 Kết quả khi 1/ 300ms và 1/  700 ms

 Nếu 1/ 280ms

và 1/  720 ms

ta có kết quả như hình 4.12:

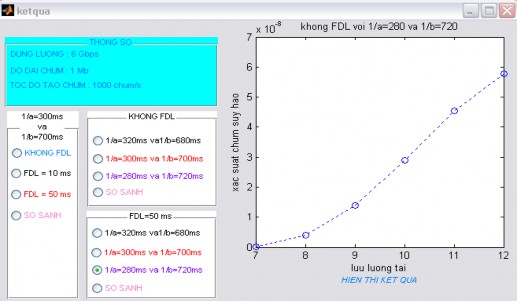
Hình 4.12. Kết quả khi 1/ 280ms và 1/  720 ms

 So sánh các kết quả như hình 4.13.

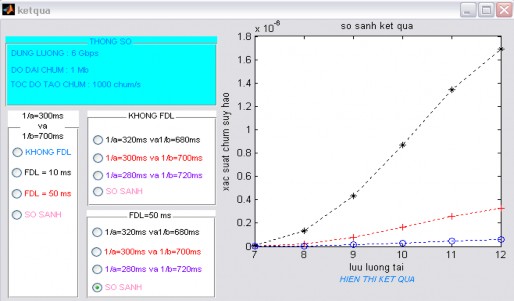
Hình 4.13 Kết quả so sánh

Hình 4.13 thể hiện kết quả xác suất chùm suy hao khi thay đổi giá trị

1/

nhưng trong trường hợp này với việc kết hợp sử dụng FDL=50ms. Với việc sử dụng FDL=50ms thì xác suất chùm suy hao lại càng giảm khi ta giảm dần giá trị 1/.

Ví dụ cụ thể như: lưu lượng tải là 8 nếu không FDL và 1/ 320ms thì xác suất

chùm suy hao đạt giá trị

0.17 10 6 .

0.5 10 6

, nếu FDL=50ms và

1/ 320ms

thì có giá trị

Kết luận chung:

Nội dung tính toán ở trên đã thể hiện xác suất chùm suy hao khi sử dụng phương pháp làm lệch hướng đi trong mạng OBS, kết quả cho thấy khi sử dụng FDL thì giảm được xác suất chùm suy hao, nếu càng tăng giá trị FDL thì thể hiện càng rõ

nét. Mặt khác với việc kết hợp giảm giá trị hao càng được giảm.

1/

và tăng FDL thì xác suất chùm suy

KẾT LUẬN VÀ HƯỚNG PHÁT TRIỂN ĐỀ TÀI

Trong đồ án này đã chỉ ra rằng mạng OBS thực hiện làm lệch hướng đi của chùm đồng nghĩa với việc giải quyết nghẽn chùm. Điều quan trọng để thiết kế lựa chọn tuyến tối ưu dựa trên kết hợp một số thông số như là: khoảng cách tuyến, xác suất chùm suy hao trên tuyến lựa chọn.

Điều đáng quan tâm trong nội dung của thuật toán là đưa ra quyết định có nên làm lệch hướng hay không, dựa trên cơ sở khoảng cách từ nút nghẽn đến nút nguồn và cũng như khả năng chặn chùm của tuyến từ nút nghẽn đến đích. Và thuật toán kiểm tra ngưỡng quyết định có làm lệch hướng chùm hay loại bỏ và gửi lại từ nguồn.

Sau đây, em xin nêu ra một số hướng phát triển cho đề tài:

 Tăng số lượng bước sóng trên mỗi liên kết để có thể giảm nghẽn trong mạng và phân tích ảnh hưởng của số lượng bước sóng đến tốc độ suy hao chum.

 Nghiên cứu nhiều hơn công dụng của FDL( trên mỗi bước sóng, trên mối port) trong mức độ chặn chùm và lưu lượng đưa vào mạng.

 Quan tâm đến những giao thức định tuyến để thực hiện trao đổi những thông tin của nút, của liên kết trong mạng.

DANH MỤC TÀI LIỆU THAM KHẢO

[1] Đặng Thanh Chương, Vũ Duy Lợi, Võ Viết Minh Nhật, Mô hình phân tích định tuyến lệch hướng kết hợp với chuyển đổi bước sóng nhằm giải quyết tắc nghẽn trên mạng chuyển mạch chùm quang OBS, Kỷ yếu Hội thảo quốc gia “Một số vấn đề chọn lọc của Công nghệ thông tin và truyền thông”, pp. 107-118, Hưng Yên, 19-20/08/2010.

[2] Đặng Thanh Chương, Mô hình hàng đợi phân tích ảnh hưởng của sự kết hợp định tuyến lệch hướng và bộ đệm FDL trong giải quyết tắc nghẽn trên mạng chuyển mạch chùm quang, Tạp chí Khoa học (Đại học Huế), 2011, Số 65, pp 19-29.

[3] Đặng Thanh Chương, Vũ Duy Lợi, Võ Viết Minh Nhật, Phân tích mô hình kết hợp giữa định tuyến lệch hướng và đường trễ quang FDL nhằm giải quyết vấn đề tắc nghẽn trên mạng chuyển mạch chùm quang OBS, Tạp chí Tin học và điều khiển học, T.27, S.1, (2011), 61-71.

[4] Đặng Ngọc Khoa & Thân Thanh Hương “ MATLAB VÀ ỨNG DỤNG TRONG VIỄN THÔNG” nhà xuất bản quốc gia HỒ CHÍ MINH

PHỤ LỤC

function varargout = ketqua(varargin) gui_Singleton = 1;

gui_State = struct('gui_Name', mfilename, ... 'gui_Singleton', gui_Singleton, ... 'gui_OpeningFcn', @ketqua_OpeningFcn, ... 'gui_OutputFcn', @ketqua_OutputFcn, ... 'gui_LayoutFcn', [] , ...

'gui_Callback', []); if nargin && ischar(varargin{1})

gui_State.gui_Callback = str2func(varargin{1}); end

if nargout

[varargout{1:nargout}] = gui_mainfcn(gui_State, varargin{:}); else

gui_mainfcn(gui_State, varargin{:}); end

function ketqua_OpeningFcn(hObject, eventdata, handles, varargin) handles.output = hObject;

guidata(hObject, handles); varargout{1} = handles.output;

function NUT1_Callback(hObject, eventdata, handles) set(handles.NUT1,'Value',1); set(handles.NUT2,'Value',0); set(handles.NUT3,'Value',0); set(handles.NUT4,'Value',0); set(handles.NUT5,'Value',0); set(handles.NUT6,'Value',0); set(handles.NUT7,'Value',0); set(handles.NUT8,'Value',0); set(handles.NUT9,'Value',0); set(handles.NUT10,'Value',0);

set(handles.NUT11,'Value',0); set(handles.NUT12,'Value',0);

%THONG SO C = 6;

L = 5;

lamda = 1000;

%KHI KHONG SU DUNG FDL B = 0;

n0 = 10^3.*C./(lamda.*L);

% DIEU KIEN n0+1<i i=7:12;

Ti=B.*C./(lamda.*L.*(i-n0).*(i-n0+1)); a=3.333;

b=1.4286;

% DIEU KIEN n>i n=25;

p=factorial(n)./(factorial(i).*factorial(n-i)).*((b./(a+b)).^i).*((b./(a+b)).^(n-i)); Pl=p.*exp(-i.*a.*Ti);

%VE HAM Pl THEO i

h=plot(i,Pl,'b*-');

title('ket qua khong su dung FDL'); xlabel('luu luong tai');

ylabel('xac suat chum suy hao');

%HIEN THI TREN HE TOA DO

axes(h)

function NUT2_Callback(hObject, eventdata, handles) set(handles.NUT1,'Value',0); set(handles.NUT2,'Value',1); set(handles.NUT3,'Value',0); set(handles.NUT4,'Value',0); set(handles.NUT5,'Value',0); set(handles.NUT6,'Value',0);

set(handles.NUT7,'Value',0); set(handles.NUT8,'Value',0); set(handles.NUT9,'Value',0); set(handles.NUT10,'Value',0); set(handles.NUT11,'Value',0); set(handles.NUT12,'Value',0);

%THONG SO C = 6;

L = 1;

lamda = 1000;

%KHI SU DUNG FDL = 10 ms B1=10;

n0 = 10^3.*C./(lamda.*L);

%CHON i THOA DIEU KIEN i>n0+1 i=7:12;

Ti1=B1.*C./(lamda.*L.*(i-n0).*(i-n0+1)); a=3.333;

b=1.4286;

%CHON n THOA DIEU KIEN n>i n=25;

p=factorial(n)./(factorial(i).*factorial(n-i)).*((b./(a+b)).^i).*((b./(a+b)).^(n-i)); Pl1=p.*exp(-i.*a.*Ti1);

%VE HAM Pl1 THEO i

g=plot(i,Pl1,'ko--');

title('ket qua khi FDL=10ms'); xlabel('luu luong tai'); ylabel('xac suat chum suy hao');

%HIEN THI TREN HE TOA DO

axes(g)

function NUT3_Callback(hObject, eventdata, handles) set(handles.NUT1,'Value',0); set(handles.NUT2,'Value',0);