Phân Tích Hiệp Phương Sai Giữa Anh Chị Em Ruột Và Nửa Ruột Thịt

do ảnh hưởng cộng gây nên), ký hiệu rE.

Theo công thức của hệ số tương quan, ta có: CovP(X,Y) CovP(X,Y)

rP = = [4.12]

VP(X) VP(Y) P(X) P(Y)

CovA(X,Y) CovA(X,Y)

rA = = [4.13]

VA(X) VA(Y) A(X) A(Y)

CovE(X,Y)	CovE(X,Y)
=		[4.14]
VE(X) VE(Y)	E(X) E(Y)

Có thể bạn quan tâm!

Xem toàn bộ 128 trang tài liệu này.

rE =

Do: CovP(X,Y) = CovA(X,Y) + CovE(X,Y)

nên:

rP P(X) P(Y) = rA A(X) A(Y) + rE E(X) E(Y)

Do: h2 = 2 /2 ; nên: 

= hP

Đặt e2 = 1 - h2 = 2 /2

- 2

/2 = (2

- 2

) /2

= 2 /2

; nên: E

= eP

Thay vào công thức trên ta có:

rP P(X)P(Y) = rAhxP(X)hYP(Y) + rEeXP(X)eYP(Y)

rP = rA hX hY + rE eX eY [4.15]

Như vậy, nếu h2 và h2

đều nhỏ, rE

sẽ quyết định rP, ngược lại

nếu h2

và h2 đều lớn, r

sẽ quyết định rP.

2.2. Cách tính hệ số tương quan di truyền

Các phương pháp ước tính hệ số tương quan di truyền tương tự như các phương pháp ước tính hệ số di truyền.

2.1.1. Hồi quy con theo bố (hoặc mẹ)

Xét các cặp bố (hoặc) mẹ và con với các giá trị kiểu hình của 2 tính trạng X và Y như sau:

Tính trạng X	Tính trạng Y
Bè (hoỈc mĐ)	PX1 = GX1 + EX1	PY1 = GY1 + EY1
Con	PX2 = GX2 + EX2	PY2 = GY2 + EY2

Các hệ số hồi quy cần tính:

- Hồi quy giá trị kiểu hình tính trạng Y ở con theo tính trạng X ở bố (hoặc mẹ): bP(X1)P(Y2)

- Hồi quy giá trị kiểu hình tính trạng X ở con theo tính trạng Y ở bố (hoặc mẹ): bP(Y1)P(X2)

- Hồi quy giá trị kiểu hình tính trạng X ở con theo tính trạng X ở bố (hoặc mẹ): bP(X1)P(X2)

- Hồi quy giá trị kiểu hình tính trạng Y ở con theo tính trạng Y ở bố (hoặc mẹ): bP(Y1)P(Y2)

Hệ số tương quan di truyền:

bP(X1)P(Y2) bP(Y1)P(X2)

rA =

2 2

bP(X1)P(X2) bP(Y1)P(Y2) CovP(X1,Y2) CovP (Y1,X2)

P(X1) P(Y1)

CovP (X2, X1) CovP (Y1,Y2)

2 2

P(X1) P(Y1)

CovG(X1,Y2) CovG(Y1,X2)

CovG(X2,X1) CovG(Y1,Y2)

Thay các giá trị hiệp phương sai di truyền giữa bố (hoặc mẹ) và con vào ta có:

rA =

(1/2A(X,Y) + 1/4AA(X,Y) + 1/8AAA(X,Y)+...)

(1/22

A(X)

+1/42

AA(X)

+1/82

AAA(X)

+...)(1/22

A(Y)

+1/42

AA(Y)

+1/82

AAA(X,Y)

+...)

A(X,Y) + 1/2AA(X,Y) + 1/4AAA(X,Y) +...

rA = [4.16]

(2

A(X)

+1/22

AA(X)

+1/42

AAA(X)

+...)( 2

A(Y)

+1/22

AA(Y)

+1/42

AAA(X,Y)

+...)

2.1.2. Phân tích hiệp phương sai giữa anh chị em ruột và nửa ruột thịt

Mô hình thống kê 2 tính trạng X và Y như sau: Tính trạng X: Xijk = + Si + Dij + Eijk

Tính trạng Y: Yijk = ' + S'i + D'ij + E'ijk

Nếu tính trạng X và Y xác định được trên 2 con vật là anh chị em ruột, vậy hiệp phương sai giữa 2 anh chị em ruột:

Cov(Xijk,Yijl) = Cov(+Si+Dij+Eijk,'+S'i+D'ij+E'ijk)

= Cov(Si,S’i) + Cov(Dij,D’ij)

= s(XY) + d(XY)

Nếu tính trạng X và Y xác định được trên 2 con vật là anh chị em nửa ruột thịt, vậy hiệp phương sai giữa 2 anh chị em nửa ruột thịt:

Cov(Xijk,Yiml) = Cov((+Si+Dij+Eijk,'+Si+D'im+E'iml)

= Cov(Si,S'i)

= s(XY)

Thuật toán phân tích hiệp phương sai 2 nhân tố phối giống phân nhóm (heirarchical mating)

được sử dụng để phân tích các số liệu thu được của 2 tính trạng X và Y của đời con ở các nhóm bố -mẹ khác nhau:

Số hiệu bố

Số hiệu mẹ	Số hiệu con	Năng suất con(X)	Năng suất con (Y)
1	11	111	X111	Y111
1	...	...	...	...
1	11	11k	X11k	Y11k
1	1m	1m1	X1m1	Y1m1
1	...	...	...	...
1	1m	1mk	X1mk	Y1mk
...	...	...	...	...
n	n1	n11	Xn11	Yn11
n	...	...	...	...
n	n1	n1k	Xn1k	Xn1k
n	...	...	...	...
n	nm	nm1	Xnm1	Xnm1
n	...	...	...	...
n	nm	nmk	Xnmk	Xnmk

Kết quả phân tích hiệp phương sai thu được như sau:

Nguồn biến đổi Độ tự do Tích chéo trung bình Ước tính hiệp phương sai

Giữa các bố

	s - 1		MCPs	e(XY) +		td(XY) + tds(XY)
Giữa các mẹ		s(d-1)		MCPd	e(XY)	+	td(XY)
trong các bố

Giữa các đời con sd(t - 1) MCPe e(XY)

trong các bố

e(XY) = MCPe

d(XY) = (MCPd - MCPe)/t

s(XY) = (MCPs - MCPd)/td

Từ kết quả phân tích phương sai đối với tính trạng X và tính trạng Y ta thu được:

Tính trạng X Tính trạng Y

Từ thành phần phương sai của bố 2

Từ thành phần phương sai của mẹ 2

Từ thành phần phương sai ngẫu nhiên 2

s(X)

d(X)



s(Y)

d(Y)

2

e(X) e(Y)

Sử dụng các kết quả phân tích phương sai và hiệp phương sai, ước tính được 3 giá trị của hệ số tương quan di truyền:

Từ thành phần phương sai và hiệp phương sai của bố:

s(XY)

rA(XY) =

2

s(X)

2

s(Y)

A(X,Y) + 1/4AA(X,Y) + 1/8AAA(X,Y) +...

rA(XY) = [4.17]

(2

A(X)

+1/42

AA(X)

+1/82

AAA(X)

+...) (2

A(Y)

+1/42

AA(Y)

+1/82

AAA(Y)

+...)

Từ thành phần phương sai và hiệp phương sai của mẹ:

s(XY)

rA(XY) =

2

s(X)

2

s(Y)

A(X,Y) + 1/4AA(X,Y) + 1/8AAA(X,Y) +...

rA(XY) = [4.18]

(2

A(X)

+1/42

AA(X)

+1/82

AAA(X)

+...) (2

A(Y)

+1/42

AA(Y)

+1/82

AAA(X,Y)

+...)

Từ thành phần phương sai và hiệp phương sai của bố và của mẹ:

s(XY) d(XY)

rA(XY) =

2

s(X)

+ 2

d(X)

2

s(Y)

+ 2

d(Y)

A(X,Y) + 1/2AA(X,Y) + 1/2D(X,Y) +...

rA(XY) = [4.19]

(2

A(X)

+1/22

AA(X)

+1/22

D(X)

+...) (2

A(Y)

+1/22

AA(Y)

+1/42

D(Y)

+...)



Phương sai và hiệp phương sai kiểu hình:

2 = 2

+ 2

P(X,Y) = s(X,Y) + d(X,Y) + e(X,Y)

Do đó, tương quan kiểu hình sẽ bằng:

P(XY)

rP(XY) =

2

P(X)

2

P(Y)

s(X,Y) + d(X,Y) + e(X,Y) +...

rP(XY) = [4.20]

(2

s(X)

+ 2

d(X)

+ 2

e(X)

+...) (2

s(Y)

+ 2

d(Y)

+ 2

e(Y)

+...)

Phương sai di truyền cộng bằng:

2 = 42 = 42 = 2(2 +2 )

A s d s d



Phương sai ngoại cảnh bằng:

2 = 2

- 42

= 2 + 2 - 32

= 2

- 42 = 2 + 2 - 32

P d s e d

= 2

- 2(2 + 2 ) = 2 + 2 - 2

P s d e s d

rE(XY) =

d(X,Y) + e(X,Y) - 3s(X,Y) +...

(+ - 3+...) (+ - 3+...)

2 2 2 2 2 2

d(X) e(X) (2s(X) d(Y) e(Y) s(Y)

s(X,Y) + e(X,Y) - 3d(X,Y) +...

rE(XY) =

(2

s(X)

+ 2

e(X)

- 32

d(X)

+...) (2

s(Y)

+ 2

e(Y)

- 32

d(Y)

+...)

e(X,Y) - s(X,Y) - d(X,Y) +...

rE(XY) = [4.21]

(- - +...) (-- +...)

2 2 2 2 2 2

e(X) s(X) d(X) e(Y) s(Y) d(Y)

Bảng 4.2. Hệ số tương quan kiểu hình, di truyền và ngoại cảnh của một số tính trạng

Loại gia súc (Tác giả, năm)

rP	rA	rE
Bò (Barker, 1966)
- Sản lượng sữa - Tỷ lệ mỡ sữa	- 0,26	- 0,38	- 0,18
- Sản lượng sữa kỳ I - Sản lượng sữa kỳ II	0,40	0,75	0,26
Gà
- Khối lượng cơ thể - Khối lượng trứng	0,33	0,42	0,23
- Khối lượng cơ thể - Sản lượng trứng	0,01	- 0,17	0,08
- Khối lượng trứng - Sản lượng trứng	- 0,05	- 0,31	0,02
Lỵn:
- Tăng trọng - Độ dày mỡ lưng	0,00	0,13	-0,18
- Tăng trọng - Hiệu quả sử dụng thức ăn	0,66	0,69	0,64

A. Ducos (1994) đã mô tả bằng sơ đồ hệ số di truyền, hệ số tương quan di truyền giữa các tính trạng tốc độ sinh trưởng, hiệu quả chuyển đổi thức ăn, chất lượng thịt xẻ và chất lượng thịt ở lợn như sau:

h2 = 0,30

Tốc độ sinh trưởng

rA = 0,15 - ++ rA = 0,60

h2 = 0,50 h2 = 0,30

Chất lượng thịt xẻ

Hiệu quả chuyển đổi thức ăn

rA = 0,20 _ 0 _ rA = 0,10

Chất lượng thịt

h2 = 0,23

Hình 4.2. Sơ đồ mối quan hệ di truyền giữa một số tính trạng của lợn (Ducos, 1994)

Sơ đồ cho thấy hệ số tương quan di truyền âm giữa các tính trạng chất lượng thịt xẻ (các tỷ lệ thịt giết mổ, độ dày mỡ...) và chất lượng thịt (năng suất các sản phẩm của công nghệ chế biến thịt), cũng như giữa chất lượng thịt xẻ và tốc độ sinh trưởng (khối lượng con vật, tăng trọng). Các mối tương quan này cho thấy, việc chọn lọc nhằm nâng cao chất lượng thịt sẽ làm

giảm thấp chất lượng thịt xẻ, việc chọn lọc nâng cao tốc độ sinh trưởng cũng làm giảm thấp chất lượng thịt xẻ. Do vậy giải pháp tốt nhất là phải lựa chọn một phương pháp chọn lọc để có thể cùng một lúc cải tiến được các tính trạng đã nêu trên.

3. Hệ số lặp lại

3.1. Khái niệm

Khi một tính trạng được quan sát nhiều lần trên một cá thể, giá trị kiểu hình của mỗi lần quan sát ngoài tác động của ngoại cảnh chung (còn gọi là ngoại cảnh thường xuyên) còn chịu

ảnh hưởng của ngoại cảnh đặc biệt (còn gọi là ngoại cảnh tạm thời), ta có thể tính toán được hệ số lặp lại của tính trạng đó.

Giả sử ta có i cá thể, mỗi cá thể có k lần quan sát được nhắc lại:

Số hiệu cá thể

Số lần nhắc lại	Quan sát thu được
1	11	X11
...	...	...
1	1m	X1m
2	21	X21
...	...	...
2	2m	X2m
...	...	...
n	n1	Xn1
...	...	...
n	nm	Xnm

Phương sai kiểu hình của tất cả các quan sát của tất cả các cá thể bao gồm phương sai giữa các cá thể (do di truyền khác nhau giữa các cá thể và do ngoại cảnh chung gây nên) và phương sai trong từng cá thể (do ngoại cảnh khác nhau giữa các lần nhắc lại quan sát gây nên):

VP = VGiữa các cá thể + VTrong từng các thể

Sai lệch ngoại cảnh bao gồm sai lệch ngoại cảnh chung (ngoại cảnh thường xuyên) và ngoại cảnh riêng (ngoại cảnh tạm thời):

E = Eg + Es = Ep + Et

Hệ số lặp lại (ký hiệu ) là tỷ số giữa tổng của phương sai di truyền, phương sai ngoại cảnh chung và phương sai kiểu hình:

VG + VEg

= [4.22]

So với hệ số di truyền, hệ số lặp lại luôn bằng hoặc lớn hơn vì so với hệ số di truyền theo nghĩa rộng, trong công thức trên, tử số của hệ số lặp lại có thêm phần phương sai ngoại cảnh chung. Người ta thường gọi hệ số lặp lại là giới hạn trên của hệ số di truyền: h2

3.2. Cách ước tính

Có 2 phương pháp ước tính hệ số lặp lại:

- Ước tính hệ số lặp lại trên cơ sở hệ số tương quan giữa các số liệu quan sát được của 2 lần nhắc lại

- Ước tính hệ số lặp lại bằng phươngpháp phân tích phương sai các số liệu quan sát được của 2 hay nhiều lần nhắc lại.

Trên thực tế ta thường dùng phương pháp phân tích phương sai 1 nhân tố để ước tính hệ số lặp lại. Nếu có i cá thể, mỗi cá thể có k lần nhắc lại các quan sát (số liệu cân bằng), kết quả phân tích phương sai thu được như sau:

e i

2

Nguồn biến đổi Độ tự do Bình phương trung bình Ước tính phương sai Giữa các cá thể i - 1 MSi 2 + k2 Giữa các lần nhắc lại k(i - 1) MSe 2

e = MSe

2

i = (MSi - MSe)/k

2 2 2

P = i + e



VÝ dô:

=

2 2

i + e

Ước tính hệ số lặp lại một tính trạng xác định được ở 6 cá thể, mỗi cá thể có 10 quan sát nhắc lại (trường hợp số liệu cân bằng), tổng số 60 quan sát như sau:

Cá thể

28	26	19	17	18	20
22	31	26	24	20	19
22	27	27	21	22	26
25	28	23	21	20	22
24	25	19	20	20	23
23	22	21	23	21	20
26	29	18	24	20	25
30	22	20	26	20	25
22	22	21	25	18	20
23	30	22	27	17	17
Xm	245	262	216	228	196	217

Số cá thể: i = 6

Số quan sát nhắc lại của mỗi các thể: k = 10 Tổng số quan sát: ik = 6 x 10 = 60

Xnm = 28 + 22 + ... + 17 = 1.364 (Xnm)2/ik = 1.3642/60 = 31.008,266

X2nm = 282 + 222 + ... + 172 = 31.718

(Xm)2/k = 2452/10 + 2622/10 + ... + 2172/10 = 31.281,4

Tổng bình phương giữa các cá thể:

2 2

(Xm) /k - (X ) /ik = 31.281,4 - 31.008,266 = 273,134

Tổng bình phương giữa các lần nhắc lại trong các cá thể:

nm m

X2 - (X )2/k = 31.718 - 31.281.4 = 436,6

Bảng phân tích phương sai:

Nguồn biến đổi Bậc tự do Tổng bình phương Bình phương trung bình Giữa các cá thể 6-1=5 273,134 273,134/5 = 54,6268

Giữa các lần nhắc lại 6(10-1)=54 436,6 436,6/54 = 8,0852 Phương sai giữa các cá thể: 2 = 8,0852

Phương sai giữa các lần nhắc lại: 2 = (54,6268 - 8,0852)/10 = 4,6542 Hệ số lặp lại:

i i e

= 2 /(2 +2 ) = 4,6542/(8,0852+4,6542) = 0,365

Hệ số lặp lại một số tính trạng năng suất bò sữa như sau (Barker, 1960): Sản lượng sữa kỳ I và kỳ II: = 0,40

Tỷ lệ mỡ sữa kỳ I và kỳ II : = 0,67

3.3. ứng dụng của hệ số lặp lại

Khi các quan sát được nhắc lại nhiều lần trên một các thể, chẳng hạn bò sữa có số liệu năng suất sữa của nhiều chu kỳ vắt sữa, lợn nái có số liệu về số con đẻ ra trong nhiều lứa đẻ, sử dụng hệ số lặp lại sẽ tăng được độ chính xác của việc đánh giá giá trị kiểu hình của con vật. Nguyên nhân như sau:

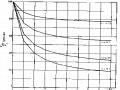
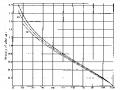
Khi các tính trạng của một cá thể được nhắc lại nhiều lần, phương sai sai lệch ngoại cảnh riêng (VEs) sẽ giảm đi. Giả sử mỗi cá thể có m lần quan sát được nhắc lại, phương sai kiểu hình trung bình của m lần nhắc lại này ký hiệu là VP(m) , phương sai sai lệch ngoại cảnh riêng sẽ giảm đi m lần, do vậy:

VP(m) = VG + VEg + 1/m VEs [4.23]

Số lần nhắc lại m càng tăng, phương sai sai lệch ngoại cảnh riêng càng giảm, dẫn tới phương sai kiểu hình trung bình của m lần nhắc lại giảm, điều đó có nghĩa là giá trị kiểu hình trung bình trong m lần nhắc lại ít bị phân tán hơn, nó biểu thị cho một giá trị kiểu hình chính xác hơn.

Do: VG + VEg + VEs = VP

VG + VEg VEs

+ = 1

VP VP

VEs

= 1 -

VG + VEg

= 1 - 

Do đó:

VP VP

VEg = (1 - )VP [4.24]

Do: VG + VEg = VP