Biện Pháp 5: Bồi Dưỡng Khả Năng Gắn Kết Toán Học Với Thực Tiễn Cho Svsp

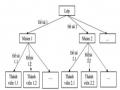
Sáng tạo bài toán afin mới :

Khi chọn BD làm đường thẳng vô tận, ta có :

Bài toán 1 :Trong mặt phẳng afin cho hình thang MNIJ( MJ//NI) có các cạnh bên cắt nhau tại K. Trên hai đáy lấy điểm A, C(A MJ, CNI) sao cho

AI//CJ. Gọi Q là điểm bất kì thuộc AI, KQ cắt CJ tại P. Chứng minh rằng MP// NQ.

Khi chọn BC làm đường thẳng vô tận ta có bài toán :

Bài toán 2 : Trong mặt phẳng afin cho hình thang BOMJ(BO//MJ) có các cạnh bên cắt nhau tại P. Lấy điểm A bất kì thuộc MJ, trên AD lấy Q. Đường thẳng qua M song song với OQ cắt PQ tại K. Chứng minh KJ//AD.

Chọn AB làm đường thẳng vô tận , ta có :

Bài toán 3 : Trong mặt phẳng afin cho tứ giác KNQI, trên IQ lấy điểm D. Qua D kẻ đường thẳng song song với IN cắt NQ tại O. Qua O kẻ đường thẳng song song với KN cắt KQ tại P. Chứng minh DP//IK.

Bài toán 4 :Chứng minh rằng nếu hai tam giác có các cạnh tương ứng song song thì đường thẳng nối các đỉnh tương ứng đồng quy.

Có thể bạn quan tâm!

Xem toàn bộ 200 trang tài liệu này.

Bài toán đối ngẫu : Trong mặt phẳng xạ ảnh cho tứ giác ABCD ; I= AC∩BD. E,F là 2 điểm bất kì trong mặt phẳng sao cho E, I, F thẳng hàng ; J=AE∩FC ;K=ED∩BF. Chứng minh rằng JK, AD, BC đồng quy.

(2) Sử dụng bất biến của các phép biến đổi sáng tạo bài toán mới Ví dụ 2( Ví dụ 1.6)

(3) Sử dụng các công cụ của HHCC sáng tạo phương pháp mới giải bài toán HHPT

Ví dụ 3

Đối với các bài toán liên quan tới bất biến Afin chúng ta có thể sử dụng một

phép biến đổi Afin thường gặp, đó là Phép chiếu song song. Có thể sử dụng tính chất của một phép chiếu song song phù hợp để giải quyết vấn đề hoặc sử dụng mô hình tương đương Afin. Cách giải của hình học cao cấp này cũng có thể chuyển thành ngôn ngữ PT.

Ta xét cụ thể:

Phép chiếu song song

Định nghĩa: Cho α là một m- phẳng trong không gian Afin An; là một không gian con bù tuyến tính với không gian liên kết của α trong An.

Ánh xạ f : An → α biến điểm M thuộc An thành M’ là giao của m- phẳng α

và (n-m) - phẳng qua M có phương gọi là phép chiếu song song cơ sở α , phương .

Tính chất

- Phép chiếu song song là một ánh xạ Afin.

- Phép chiếu song song từ một m – phẳng α đến một m- phẳng α’ cùng có không gian liên kết bù tuyến tính với là một đẳng cấu Afin.

- Đặc biệt, nếu α và α’ là 2 mặt phẳng trong không gian Afin 3 chiều; là một không gian con 1 chiều không thuộc không gian liên kết với α và α’ thì phép chiếu song song từ α đến α’ là đẳng cấu Afin.

Như vậy mọi bất biến Afin đều bất biến qua phép chiếu song song từ mặt phẳng đến mặt phẳng thỏa mãn điều kiện trên.

- Luôn tồn tại phép chiếu song song biến tam giác thành tam giác đều, hình bình hành thành hình vuông, elip thành đường tròn.

Cụ thể :

a) Tam giác thành tam giác đều :

Cho tam giác ABC ; Trên mặt phẳng không chứa tam giác dựng tam giác ABC’ đều. Xét phép chiếu song song từ ( ABC ) đến ( ABC’) phương CC'sẽ

biến tam giác ABC thành tam giác đều ABC’.

b) Hình bình hành thành hình vuông

Cho hình bình hành ABCD; Trên mặt phẳng không chứa hình bình hành dựng hình vuông ABC’D’. Xét phép chiếu song song từ (ABCD) đến (ABC’D’)

phương CC'sẽ biến hình bình hành ABCD thành hình vuông ABC’D’.

c) Elip thành hình tròn :

Cho elip tâm O. Trong mặt phẳng Q không song song với mặt phẳng P chứa elip và qua điểm A thuộc elip dựng đường tròn tâm O’,tiếp xúc với elip tại A. Xét phép chiếu song song từ P tới Q phương OO’, biến elip thành đường tròn.

Ứng dụng phép chiếu song song giải toán hình học phổ thông

Ví dụ 1. Qua mỗi đỉnh của tam giác ABC kẻ 2 đường thẳng chia cạnh đối diện của tam giác thành 3 phần bằng nhau. Chứng minh rằng các đường chéo nối các đỉnh đối diện của lục giác được tạo thành từ 6 đường thẳng đó đồng quy tại 1 điểm.

Lời giải. Gọi là mặt phẳng chứa tam giác ABC, ’ là mặt phẳng qua BC, khác . Trong ’ lấy điểm A’ sao cho tam giác A’BC là tam giác đều. Xét phép chiếu song song từ lên ’ theo phương AA’. Do phép chiếu song

song bảo toàn tỉ số đơn, sự đồng quy nên nó biến tam giác ABC thành tam giác A’BC và 6 đường thẳng tương ứng thành các đường thẳng có tính chất tương tự trên tam giác A’BC. Ta chỉ cần chứng minh bài toán trên tam giác đều A’BC.

Hình 2

M P'

Thật vậy, lấy P’ là trung điểm của BC. Vì B và C , R’ và N là 2 cặp điểm đối xứng qua A’P’, ta có các đường thẳng BN và CR’đối xứng qua A’P’ nên giao điểm của chúng là X’ thuộc A’P’. Tương tự, điểm X là giao của CR và BR’ cúng thuộc A’P’. Hay nói cách khác XX’ là đường cao tam giác A’BC.

Tương tự ta có YY’ và ZZ’ là các đường cao còn lại. Do 3 đường cao của tam giác đồng quy, ta có điều phải chứng minh.

Ví dụ 2. Chứng minh rằng trong một tứ diện bất kỳ, tổng của tích 2 cặp cạnh

đối lớn hơn tích của cặp cạnh đối còn lại.

Định hướng :

Trong tứ diện ABCD, cần chứng minh AC.BD < AB.CD + AD.BC. Ta đã biết bất đẳng thức Ptôlêmê đối với tứ giác :

trong tứ giác ABCD, ta có AC.BD ≤ AB.CD + AD.BC.

Liên tưởng trên dẫn tới việc cần tìm mối liên hệ giữa độ dài các cạnh của tứ diện ABCD với độ dài các cạnh của một tứ giác. Từ đó liên hệ với việc cần sử dụng một phép chiếu song song phù hợp.

Lời giải

Hình 3

Xét mặt phẳng α song song với hai cạnh AC và BD của tứ diện. Xét phép chiếu vuông góc xuống α biến tứ diện ABCD thành tứ giác A’B’C’D’.

Do α song song với AC và BD, ta có AC = A’C’ ; BD = B’D’ ; AB >A’B’ ; AD>A’D’ ; BC > B’C’ ; CD > C’D’ ;

Theo định lý Ptolemy, A’C’.B’D’ ≤ A’B’.C’D’ + A’D’.B’C’

Do đó : AC.BD < AB.CD + AD.BC

Biện pháp 4 nhằm tổ chức cho SV học tập một cách chủ động, sáng tạo, thể hiện được khả năng của mình đồng thời giúp họ nắm được cách thức tổ chức hoạt động nhóm để sau này họ có thể vận dụng vào dạy học Toán ở trường PT. Cách dạy học này thể hiện tính phân hóa cao trong SV. Việc tổ chức thảo luận trong nhóm với sự có mặt của giảng viên nhằm tối đa hóa số lượng SV được báo cáo trước đám đông bởi vì số SV được báo cáo trước lớp là không nhiều, ngoài ra giảng viên có thể đánh giá được chính xác hơn năng lực và đóng góp của mỗi cá nhân.

Với sự lựa chọn chủ đề hợp lí cho đối tượng SV của lớp và số lần tổ chức vừa phải thì hình thức dạy học này góp phần làm cho SV nắm vững nội dung HHCC, biết cách khai thác những hiểu biết về HHCC để giải quyết các vấn đề HHPT. Thông qua hoạt động này, việc học môn HHCC càng trở nên

hứng thú, hiệu quả hơn. Qua biện pháp, SV hình thành NL tổ chức, tự học, NL bồi dưỡng tư duy HS… và rèn luyện thêm bản lĩnh nghề nghiệp sau này.

2.2.5. Biện pháp 5: Bồi dưỡng khả năng gắn kết toán học với thực tiễn cho SVSP dựa trên tư tưởng của HHCC.

2.2.5.1. Mục tiêu của biện pháp

Biện pháp này nhằm mục đích phát triển năng lực gắn kết toán học với thực tiễn cuộc sống cũng như thực tiễn nghề nghiệp của SV.

2.2.5.2. Nội dung của biện pháp

Theo phân tích ở chương I, phần 1.5.7, giáo dục nói chung, giáo dục đại học nói riêng phải đạt được hai mục tiêu là mục tiêu lý luận và mục tiêu thực tiễn. Tức là, SV ĐH không những được trang bị kiến thức khoa học một cách có hệ thống mà còn phải là những con người có NL thực hành, áp dụng các kiến thức đã học được vào thực tiễn đời sống cũng như nghề nghiệp sau này. Do đó việc bồi dưỡng năng lực gắn kết toán học với thực tiễn cho SV là thực sự cần thiết. Bồi dưỡng cho SVSP Toán năng lực gắn kết toán học với thực tiễn có thể theo một số cách thức:

(1) Bồi dưỡng cơ sở tư duy biện chứng cho SV thông qua việc cài đặt một cách hợp lý vào các bài giảng HHCC

Toán học cũng như các môn khoa học khác đều luôn trong quá trình vận động và phát triển. Sự kế tiếp của mỗi thời kỳ tuân theo một logic nhất định phản ánh tiến trình phát triển nội tại của toán học và của những nhân tố bên ngoài, tác động vào nó. Cũng như các tri thức khác, sự phát triển của tri thức toán học mang tính biện chứng sâu sắc. Nó là quá trình vừa kế thừa vừa đổi mới về chất giữa các thời kỳ. Các tri thức toán học ở thời kỳ sau chung hơn, sâu sắc hơn, đa dạng hơn thời kỳ trước và bao quát nó như trường hợp riêng. Khi nghiên cứu lịch sử hình học, ta nhận thấy, ban đầu, các khái niệm hình học chỉ được xem xét thông qua những trường hợp riêng bằng việc quan

sát, đo đạc thực tế. Qua quá trình phát triển, các bài toán mới được hình thành bằng suy luận logic chặt chẽ, chứa những bài toán trước đó như những trường hợp riêng. Chẳng hạn, định lý Pitago được hình thành từ thời kỳ cổ đại, thế kỷ 5, 4 trước Công nguyên, với nhiều cách phát biểu khác nhau như:, “Tổng diện tích của hai hình vuông vẽ trên cạnh kề của một tam giác vuông bằng diện tích hình vuông vẽ trên cạnh huyền của tam giác này.”, “Trong một tam giác vuông, bình phương của cạnh huyền bằng tổng bình phương 2 cạnh góc

vuông”…Đến khi hình học vectơ ra đời vào thế kỷ 18, định lý này được phát

biểu dưới dạng:” Cho 2 vectơ

x, y , ta có

x y 

x y

, đẳng thức xảy ra

khi x trực giao với y ”. Khi nghiên cứu HHCC, định lý được phát biểu tổng quát với đơn hình vuông. Do đó khi nghiên cứu một vấn đề toán học nói chung, hình học nói riêng, SV cần xem xét nó trong sự vận động và phát triển và trong mối tương quan với các vấn đề khác, hay nói một cách khác, SV cần có tư duy biện chứng. Theo [67], tư duy biện chứng trong toán học cũng tuân theo quy luật từ trực quan sinh động đến tư duy trừu tượng và từ trừu tượng trở về thực tiễn, được đặc trưng bởi những khả năng nhận thức được một số quy luật sau đây:

- Quy luật vể mối liên hệ giữa nguyên nhân và kết quả: Tư duy toán học, nội dung, kiến thức toán học là một chuỗi liên kết chặt chẽ với nhau, các nội dung đã biết tạo tiền đề và giải thích cho sự xuất hiện nội dung mới và ngược lại, một nội dung mới xuất hiện có thể giải thích căn nguyên của sự tồn tại các kiến thức cũ.

- Quy luật vể mối liên hệ giữa cái chung và cái riêng: Sự sắp xếp chương trình học toán nói chung thường dẫn dắt HS đi từ các trường hợp riêng rồi khái quát, mở rộng lên những cái chung. Các phát minh toán học cũng chủ yếu là sự mở rộng từ một cái riêng đã biết thành một hay nhiều cái

chung trước đó chưa ai biết. Như vậy, thuộc tính chung, thuộc tính tổng quát chỉ có thể tìm trong những trường hợp riêng cụ thể. Từ đó, trong dạy học toán, cần luyện tập cho SV biết cách khảo sát các trường hợp riêng rồi thực hiện các thao tác phân tích, tổng hợp, so sánh, khái quát hóa… để tìm ra những thuộc tính chung của đối tượng toán học. Ngược lại, trong thực hành, phải biết áp dụng các quy luật chung để giải quyết từng trường hợp cụ thể.

- Quy luật vể mối liên hệ giữa cụ thể và trừu tượng: Quy luật này thể hiện quan điểm nhận thức được nhấn mạnh trong triết học Mác- Lênin, từ trực quan sinh động đến tư duy trừu tượng, từ tư duy trừu tượng quay trở về với thực tiễn. Sự phát triển của toán học là một quá trình trừu tượng hóa liên tiếp.

Do đó, để SV có thể nhận thức nội dung toán học cũng như có thể ứng dụng các hiểu biết ở trường ĐH vào công tác dạy học ở trường PT sau này, trong quá trình dạy học ở ĐH, GV cần quan tâm sử dụng trực quan để hỗ trợ khám phá kiến thức mới như: sơ đồ, hình vẽ, đồ thị, hình biểu diễn, hình động tạo nên từ các phần mềm dạy học… Sau đó mới từ từ nâng từng bước tư duy trừu tượng của SV thông qua các thao tác mở rộng, khái quát hóa...

- Quy luật vể mối liên hệ giữa nội dung và hình thức: Ta nhận thấy, cùng một nội dung toán học có thể có nhiều hình thức thể hiện khác nhau, ngược lại một hình thức có thể phù hợp với nhiều nội dung. Do đó với mỗi vấn đề toán học, SV cần rèn luyện khả năng nhìn nhận mối liên hệ bên trong và bên ngoài của các nội dung kiến thức, để từ đó phát hiện cách giải quyết vấn đề nhờ huy động các kiến thức liên quan và lựa chọn hình thức thể hiện phù hợp và hiệu quả nhất.

Việc dạy học toán ở các trường ĐHSP cần hướng tới việc hình thành thế giới quan duy vật biện chứng cho SV. Điều đó giúp cho thế hệ trẻ có một cách nhìn, cách xem xét hiện thực thực tiễn hơn về lĩnh vực chuyên môn của