phổ gamma, năng lượng của đỉnh xác định sự có mặt của nguyên tố trong mẫu hay còn gọi là phép định tính, và diện tích đỉnh cho phép ta định lượng nguyên tố đó [1].
1.1.2. Nguyên tắc cơ bản trong phân tich kích hoạt
Cơ sở cho việc phân tích kích hoạt neutron là dựa vào phản ứng hạt nhân của các đồng vị bia với neutron lò phản ứng hạt nhân. Phản ứng được quan tâm nhiều nhất trong phân tích kích hoạt neutron là phản ứng (n, γ) với một hạt nhân X (nhân bia) hấp thụ một neutron sẽ tạo ra một nhân phóng xạ có cùng số Z nhưng khối lượng nguyên tử tăng lên một đơn vị và phát ra bức xạ gamma tức thời. Quá trình này diễn ra như sau:
A X+ 1 n ( A+1 X)* A+1 X+γ
Trong đó:
Z 0 Z z
Có thể bạn quan tâm!
-
Đánh giá ô nhiễm trầm tích biển - 1 -
Khái Niệm Và Nguồn Gốc Hình Thành Trầm Tích Biển -
Hệ Phổ Kế Gamma Sử Dụng Detector Hpge Gmx-30190 Tại Ptn Inaa, Viện Nghiên Cứu Hạt Nhân Đà Lạt -
Hàm Lượng Trung Bình, Dải Hàm Lượng Của 26 Nguyên Tố Trong 11 Mẫu Trầm Tích Trong Core 170408-3.
Xem toàn bộ 76 trang tài liệu này.
A: số khối của nguyên tố bia, Z: số điện tích hạt nhân bia,
Ký hiệu (*) biểu diễn nhân hợp phần.
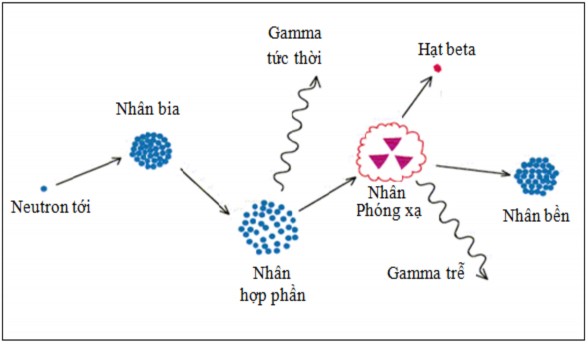
Hình 1.1. Mô hình kích hoạt nhân bia tạo nhân phóng xạ.
1.1.3 Phổ thông lượng neutron trong lò phản ứng hạt nhân
Neutron trong lò phản ứng hạt nhân ban đầu là các neutron nhanh được sinh ra từ phản ứng phân hạch nhiên liệu, sau đó các neutron này bị mất dần năng lượng và bị nhiệt hóa do tương tác với chất làm chậm (thường là nước) bên trong lò phản ứng. Do vậy ở các vị trí khác nhau trong lò phản ứng phân bố thông lượng neutron cũng bị thay đổi đáng kể. Ban đầu neutron sinh ra có năng lượng ban đầu khoảng từ 0 đến 20 Mev. Trong khoảng năng lượng này tính chất tương tác của neutron với vật chất là khác nhau trong miền năng lượng khác nhau. Vì vậy, một cách tương đối, neutron trong lò phản ứng được chia làm ba vùng năng lượng ứng với phân bố thông lượng khác nhau của mỗi vùng như sau:
- Neutron nhiệt: có năng lượng nằm trong khoảng 0 < En < 0,5 eV. Neutron nhiệt có phổ neutron phân bố theo phân bố Maxwell-Boltzmann:
dn = 2π .e
E
-
kTn .E1/ 2dE
(1.1a)
n
n (πkT ) 3/ 2
Trong đó: dn là số neutron với năng lượng khoảng từ E đến E+dE, n là số neutron tổng cộng trong hệ, k = 8,61x10-5 eV/K là hằng số Boltzmann, Tn là nhiệt độ neutron hay môi trường (đơn vị K). Ở nhiệt độ phòng thí nghiệm T = 293,6 K và E = kT = 0,0253 eV thì v = 2200 m.s-1.
Phổ thông lượng của neutron nhiệt tại nhiêt độ Tn phân bố như sau:
' (E) =
E e-E/(kTn )
(1.1b)
2
Với m
m m
(kTn )
- thông lượng neutron toàn phân theo phân bố Maxwell. Khi đó phân bố
thông lượng tương ứng là:
'm (v) = n'm (v).v
(1.1c)
- Neutron trên nhiệt: Có năng lượng trong khoảng từ 0,5 eV < E < 0,5 MeV. Vùng này còn được gọi là vùng trung gian hay vùng cộng hưởng. Sự phân bố neutron trên
nhiệt tuân theo quy luật 1/E và phân bố thông lượng neutron trên nhiệt tỉ lệ nghịch với năng lượng neutron:
e
e (E) =
E
(1.2a)
Trong đó
e (E) - thông lượng neutron trên nhiệt ở năng lượng E và
e - thông
lượng neutron trên nhiệt. Nhưng do cấu trúc vật chất trong lò phản ứng nên phổ neutron nhiệt sẽ bị lệch khỏi quy luật 1/E và được thay bởi dạng 1/E1+α:
e (E) =
e
E1+α
(1eV) α
(1.2b)
Trong đó α là hằng số đặc trưng cho sự lệch phổ lý tưởng và nó độc lập với năng lượng.
- Neutron nhanh (neutron phân hạch): là vùng neutron sinh ra trong phân hạch và có năng lượng E > 0,5 MeV. Phân bố neutron nhanh cực đại ở 0,7 MeV và được mô tả bởi phân bố Watt. Qua quá trình tương tác với chất làm chậm, neutron nhanh bị nhiệt hóa và chuyển thành neutron trên nhiệt và nhiệt. Do sự tiếp diễn của quá trình phân hạch nên cả neutron nhanh, nhiệt và trên nhiệt cùng tồn tại với nhau. Một số công thức bán thực nghiệm mô tả phổ neutron nhanh thường được dùng:
Phổ phân hạch của Watt:
2E
-E
f (E) = 0,484.f .e sinh
(1.3a)
Phổ phân hạch của Cranberg:
2,29E
-E/0,965
f (E) = 0,453.f .e sinh
(1.3b)
Phổ phân hạch của Grundl và Usner:
- 0,776E
f (E) = 0,77.f . E.e
(1.3c)
Trong đó f
và f (E)
là thông lượng neutron nhanh và thông lượng neutron
nhanh ở năng lượng E [4].
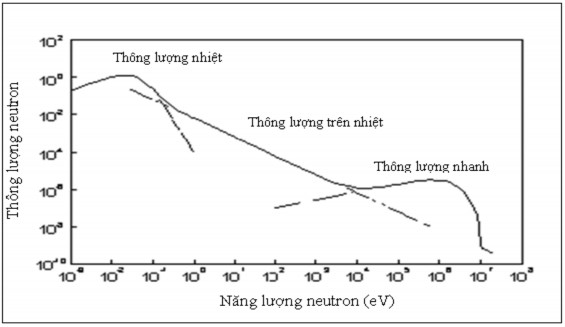
Hình 1.2 Thông lượng neutron biểu diễn theo năng lượng
1.1.4. Phương trình phân tích kích hoạt
Sau khi kích hoạt nhân bia từ lò phản ứng, và hoạt độ của các nhân hình thành được đo bằng hệ phổ kế gamma sử dụng detector bán dẫn Germanium siêu tinh khiết (HPGe), ta có được mối quan hệ giữa số đếm (Np) và tốc độ phản ứng (R) được cho bởi phương trình sau:
R = G . .σ +G .
.I(α) =
N p /t m
S.D.C.W
(1.4)
th th 0 e e
N A .θ.ε p .γ/A
Theo quy ước Hogdahl, phương trình cơ bản cho việc xác định một nguyên tố dùng phản ứng (n, γ) và phổ kế γ là:
N / t
W..NA .
..G
G I()S.D.C
(1.5)
p m M
p th th 0 e e
Với Np/tm Tốc độ xung đo được của đỉnh gamma quan tâm, đã được hiệu chỉnh cho thời gian chết và các hiệu ứng ngẫu nhiên cũng như trùng phùng thực [4].
NA : Hằng số Avogadro, Np : Diện tích đỉnh,
tm : Thời gian đo,
ti : Thời gian chiếu, td : Thời gian rã,
W : Khối lượng nguyên tố được chiếu xạ (g),
θ : Độ phổ cập đồng vị bia,
M : Khối lượng nguyên tử của nguyên tố bia, Gth : Hệ số hiệu chỉnh tự che chắn neutron nhiệt,
Ge : Hệ số hiệu chỉnh tự che chắn neutron trên nhiệt,
S = 1-exp(-λt i ) : Hệ số hiệu chỉnh thời gian chiếu,
D = exp(-λt d ) : Hệsố hiệu chỉnh thời gian phân rã,
C = [1-exp(-λt m )]/(λt m ) : Hệ số hiệu chỉnh thời gian đo,
γ : Cường độ tuyệt đối của tia gamma được đo,
εp : Hiệu suất ghi tuyệt đối tại đỉnh năng lượng,
I : Tích phân cộng hưởng hay tiết diện phản ứng trên nhiệt, α : Độ lệch khỏi quy luật 1/E tại vùng neutron trên nhiệt,
0
σ : Tiết diện phản ứng (n, γ) có vận tốc 2200ms-1.
Theo quy ước Hogdahl, phương trình cho phép ta tính hàm lượng (g) của nguyên tố như sau:
W N p / t m . M . 1
(1.6)
S.D.C N A ...p G th .th .0 G e .e .I()
1.1.5. Các phương pháp chuẩn hóa trong phân tích kích hoạt neutron
1.1.5.1. Phương pháp chuẩn hóa tuyệt đối
Hàm lượng nguyên tố ρ(μg/g) có thể thu được bằng việc chiếu kèm mẫu với một monitor chuẩn (*) được tính theo phương trình:
N p /t m
w.D.S.C
Mθ*σ* γ*
G* f+G*Q* (α)
ε p 6
ρ(μg/g) =
* . * 0
.th e 0.
* .10
(1.7)
A sp
M θσ 0γ
G thf+G eQ 0 (α) ε p
f = th
e
: Tỉ số thông lượng neutron nhiệt/trên nhiệt,
N p /t m *
A
sp
* =
W.S.D.C
: Hoạt độ riêng của monitor (*) (phân rã/giây/gam),
Q0 (α) =
I 0 (α) =
σ 0
Q0 -0,429 +
E
r
0,429 (2α+1).0,55
Với: w: Khối lượng mẫu (g), W: Khối lượng nguyên tố làm chuẩn (g).
Phương pháp chuẩn hóa tuyệt đối về mặt thực nghiệm thì rất đơn giản, chỉ cần xác định được chính xác các thông số A, θ, γ, σ0, v.v.. của nguyên tố phân tích và mornitor. Phương pháp này đòi hỏi phải sử dụng một loạt số liệu hạt nhân và số liệu thực nghiệm nên kết quả phân tích sẽ bị ảnh hưởng bởi nhiều nguồn sai số, vì vậy phương pháp này ít được sử dụng trong thực tế [5].
1.1.5.2. Phương pháp chuẩn hóa tương đối
Trong phương pháp chuẩn hóa tương đối mẫu cần đo được chiếu kèm với một mẫu chuẩn với hàm lượng Ws đã được biết trước, mẫu cần đo và và mẫu chiếu được đo trong cùng một điều kiện hình học do đó các thông số liên quan sẽ bị triêt tiêu và phương trình (1.4) sẽ được viết lại như sau:
N m /t m
ρ(μg/g) =
w.S.D.C.106
(1.8)
N p /t m *
W.S.D.C
Cần chú ý là mẫu phân tích và mẫu chuẩn sử dụng trong phương pháp này phải đồng nhất về thành phần hóa học (đồng matrice), dạng hình học mẫu, cấu hình đo, phải được hiệu chỉnh hiệu ứng tự che chắn neutron khi chiếu và hiệu chỉnh hiệu ứng suy giảm tia gamma trong khi đo mẫu.
Tuy nhiên, nhược điểm của phương pháp này là trong một số trường hợp không tìm được mẫu chuẩn có thành phần và hàm lượng tương đồng với mẫu phân tích
dẫn đến khó khăn trong việc xác định hàm lượng của nguyên tố trong mẫu phân tích.
1.1.5.3. Phương pháp chuẩn hóa đơn nguyên tố
Chuẩn hóa đơn nguyên tố là phương pháp dựa trên việc gộp các thông số hạt nhân, điều kiện chiếu xạ và điều kiện đo vào trong hệ số k, lúc đó ta tính hàm lượng nguyên tố như sau:
ρ(μg/g) =
N p /t m
w.S.D.C
. 1 .10 6
(1.9
N p /t m k
*
W.S.D.C
Đối với các nguyên tố được lựa chọn làm chuẩn thì hệ số k được xác định thông qua thực nghiệm:
M*.θ.σ.γ G f+G Q (α) ε p
k = .th e 0.
(1.10)
th e P
M.θ*.σ*.γ* G * f+G *Q(α) ε *
Ưu điểm của phương pháp này là dễ dàng cho việc phân tích tất cả các nguyên tố mà không cần mẫu chuẩn đa nguyên tố. Tuy nhiên, phương pháp này đòi hỏi ta phải xác định chính xác thư viện hệ số k cho tất cả các nguyên tố cần phân tích đối với nguyên tố đơn chuẩn, mà hệ số này lại phụ thuộc vào phổ neutron (cấu hình hệ chiếu) và hiệu suất ghi của detector (cấu hình hệ đo), do đó, khi có bất kỳ một sự thay đổi của hệ chiếu hay hệ đo thì phải xác định lại toàn bộ thư viện hệ số k, điều này làm cho phương pháp chuẩn hóa đơn nguyên tố thiếu đi tính linh hoạt [5].
1.1.5.4. Phương pháp chuẩn hóa k0
Việc sử dụng các phương pháp chuẩn hóa thông thường trong thực tế dùng để phân tích mẫu gặp phải những khó khăn nhất định về tính linh hoạt trong điều kiện đo cũng như ảnh hưởng của sai số trong phép đo. Người ta đã đưa ra một phương pháp mới là phương pháp chuẩn hóa k0-NAA để khắc phục được các nhược điểm cũng như thỏa mãn được yều cầu về độ chính xác cao, linh họat và thuận tiện trong
việc tính toán. Dựa trên hệ số k từ phương pháp chuẩn hóa đơn nguyên tố, hệ số k0 trong phương pháp chuẩn hóa k0 được xác định theo phương trình sau:
0
0
k 0 =
M *.θ.γ.σ M.θ*.γ *.σ*
(1.11)
Hằng số k0 là đại lượng độc lập với điều kiện chiếu và đo, đóng vai trò quan trọng trong việc tính toán hàm lượng mẫu phân tích.
Mẫu và mẫu chuẩn Au có thể có hình dạng và các đặc điểm hấp thụ neutron và tia gamma khác nhau. Quá trình hiệu chỉnh những khác biệt cũng được xem là một phần không thể thiếu của phương pháp k0. Mẫu phân tích chỉ cần chiếu cùng với một mẫu so sánh (hay còn gọi là lá dò thông lượng), thường là Au. Các sai số trong việc tính toán thông thường cho phép sai số của hằng số k0 là dưới 3,5% [4].
Theo quy ước Hogdahl, hằng số k0 của các đồng vị được xác định bằng thực nghiệm dựa vào phương trình:
N p /t m
W.S.D.C 1 f+Q (α) ε
k (a) =
a . .0,Au.p,Au.10 6
(1.12)
0,Au
N /t
ρ(a)
f+Q (α) ε
p m
w.S.D.C Au
0,a
p,a
Với k0 được xác định bằng thực nghiệm với độ chính xác cao (~ 1%), chất so sánh tối ưu là vàng (Au) dùng phản ứng Au 197(n, γ) Au 198 với các số liệu hạt nhân:
σ 0 = 98,65 ± 0,9 barn,
Q0 = 15,71 ± 0,28 ,
I 0 = 1550 ± 28 barn,
(a) là hàm lượng nguyên tố a có đơn vị là g/g.
Khi đó công thức tính hàm lượng của nguyên tố quan tâm a trở thành:
N p /t m
1 G * f+G *Q* (α) ε *
ρ(μg/g) =
w.S.D.C. .th e 0.
p .10 6
(1.13)
A* k 0,Au (a)
G f+G Q (α) ε
sp th e 0 p