Minh Hoạ Các Bước Cơ Bản Trong Một Hệ Thống Xử Lý Và Nhận Dạng Ảnh.

+ Liên kết m (liên kết hỗn hơp)̣ : hai điểm p và q vớ i giá tri ̣từ V là liên kết m nếu thỏa mãn môṭ trong hai điều kiêṇ sau:

- Một là: q thuộc N4(p)

- Hai là: q thuộc NP(p)

1.1.9. Biên ảnh (Image boundary)

Biên ảnh là một vấn đề chủ yếu trong phân tích ảnh, vì các kỹ thuật phân đoạn ảnh chủ yếu dựa vào biên. Theo [3], một điểm ảnh có thể coi là điểm biên nếu ở đó có sự thay đổi mạnh một cách đột ngột về mức xám. Tập hợp các điểm biên tạo thành biên hay đường bao ảnh của ảnh (Boundary). Hay nói cách khác, đường biên ảnh là nơi mà các điểm ảnh lân cận nhau có cường độ thay đổi mạnh một cách đột ngột.

Ví dụ: Trong một ảnh nhị phân, một điểm có thể gọi là biên nếu đó là điểm đen và có ít nhất một điểm trắng là lân cận.

1.2. GIỚI THIỆU CHUNG VỀ XỬ LÝ VÀ NHẬN DẠNG ẢNH

Cũng như xử lý dữ liệu bằng đồ hoạ, xử lý ảnh là một lĩnh vực của tin học ứng dụng. Xử lý dữ liệu bằng đồ họa đề cập đến những ảnh nhân tạo, các ảnh này được xem xét như là một cấu trúc dữ liệu và được tạo ra bởi các chương trình. Xử lý ảnh bao gồm các phương pháp và kỹ thuật để biến đổi, để truyền tải hoặc mã hóa các ảnh tự nhiên. Mục đích của xử lý ảnh gồm:

- Thứ nhất: Biến đổi ảnh và làm đẹp ảnh.

- Thứ hai: Tự động nhận dạng hay đoán nhận ảnh và đánh giá các nội dung của ảnh.

Thực hiện xử lý ảnh thường theo nguyên tắc: xử lý thông qua việc sử dụng hàm biến đổi ảnh. Biến đổi ảnh là quá trình thực hiện thông qua các toán tử. Một toán tử thực hiện lấy một ảnh vào đầu vào của hệ thống và tạo ra một ảnh khác theo yêu cầu xử lý. Để thực hiện quá trình biến đổi ảnh chúng ta chủ yếu quan tâm tới các toán tử tuyến tính.

Giả sử O(f) là toán tử O của một ảnh f thì toán tử O được gọi là tuyến tính nếu ta có: O[af + bg] = aO(f) + bO(g) với mọi f, g và a, b.

Trong xử lý ảnh thì các toán tử được định nghĩa là hàm trải điểm. Một hàm trải điểm của một toán tử là kết quả mà chúng ta thu nhận được sau khi thực hiện cung cấp luật của toán tử đó cho nguồn điểm: O[nguồn điểm] = hàm trải điểm. Hay chúng ta có: O[δ(x-α, y- β)] = h(x, α, y, β). Trong đó δ(x-α, y-β) là nguồn điểm có cường độ sáng bằng 1 đặt tại điểm (α,β) và nếu toán tử là tuyến tính thì ta có: O[aδ(x-α, y-β)] = ah(x, α, y, β); tức nếu tăng cường độ sáng lên a lần thì kết quả thu được cũng tăng lên a lần.

Nhận dạng ảnh là quá trình liên quan đến các mô tả đối tượng mà người ta muốn đặc tả nó. Quá trình nhận dạng thường đi sau quá trình trích chọn các đặc tính chủ yếu của đối tượng. Có hai kiểu mô tả đối tượng:

- Mô tả tham số (nhận dạng theo tham số).

- Mô tả theo cấu trúc (nhận dạng theo cấu trúc).

Nhận biết và đánh giá các nội dung của ảnh là sự phân tích một hình ảnh thành những phần có nghĩa để phân biệt đối tượng này với đối tượng khác. Dựa vào đó ta có thể mô tả cấu trúc của hình ảnh ban đầu. Có thể liệt kê một số phương pháp nhận dạng cơ bản như nhận dạng biên của một đối tượng trên ảnh, tách cạnh, phân đoạn hình ảnh, vv... Trong thực tế người ta đã áp dụng kỹ thuật nhận dạng khá thành công với nhiều đối tượng khác nhau như: nhận dạng ảnh vân tay, nhận dạng chữ cái, nhận dạng loài hoa, nhận dạng vật nuôi, vv…

Các quá trình của xử lý và nhận dạng ảnh có thể được tiến hành theo sơ đồ sau:

Thu nhận ảnh

Số hoá ảnh

Tiền xử lý ảnh

Trích chọn đặc trưng

Dữ liệu huấn luyện

Huấn luyện phân lớp

Mô hình Dữ liệu huấn luyện nhận dạng

Kết quả nhận dạng

Nhận dạng

Hình 1.1: Minh hoạ các bước cơ bản trong một hệ thống xử lý và nhận dạng ảnh.

1.2.1. Thu nhận ảnh (Image acquisition)

Trong quá trình xử lý ảnh thì trước hết là phải thu nhận ảnh (Image acquisition). Chất lượng của ảnh thu được sẽ quyết định nhiều đến kết quả của việc nhận dạng. Sau đó ảnh phải được lưu trữ theo một định dạng phù hợp với các bước xử lý sau này.

Ảnh có thể là ảnh chụp từ ống kính máy ảnh hay điện thoại. Ảnh có thể thu nhận qua camera, thường thì ảnh thu nhận qua camera là tín hiệu tương tự loại camera ống kiểu (CCIR), nhưng cũng có thể là tín hiệu số hoá loại CCD (Charge Coupled Device). Ảnh cũng có thể thu nhận từ vệ tinh qua các bộ cảm ứng (sensor), hay ảnh được quét qua máy quét scanner.

1.2.2. Số hóa ảnh (Image digitalizer)

Số hoá ảnh (Image digitalizer) là quá trình số hóa để biến đổi tín hiệu tương tự sang tín hiệu rời rạc (lấy mẫu) và số hóa bằng lượng hóa, trước khi chuyển sang giai đoạn xử lý, phân tích hay lưu trữ lại.

1.2.3. Tiền xứ lý ảnh (Image processing)

Bước này tăng khả năng nhận dạng chính xác, có vai trò nâng cao chất lượng ảnh trước khi đem phân tích và nhận dạng. Do những nguyên nhân khác nhau có thể do thiết bị thu nhận ảnh, do nguồn sáng hay do nhiễu, ảnh có thể có độ tương phản thấp, có thể bị suy

biến. Do vậy, công việc chính của tiền xử lý ảnh là nâng cao chất lượng ảnh. Nâng cao chất lượng ảnh là một bước quan trọng, nó là tiền đề cho xử lý ảnh. Mục đích chính là nhằm làm nổi bật một số đặc tính ảnh như độ tương phản, làm nổi màu, lọc nhiễu, làm trơn ảnh, khuếch đại ảnh, tăng cường ảnh hay khôi phục lại ảnh để làm nổi bật một số đặc tính chính của ảnh để nâng cao chất lượng ảnh, hay làm cho ảnh gần giống với trạng thái gốc (trạng thái trước khi ảnh bị biến dạng), vv…

Tăng cường ảnh là việc cải tiến ảnh sao cho nó thể hiện rõ được các đặc trưng của ảnh, như là điều khiển mức xám, độ tương phản ảnh, giảm nhiễu, vv... Tùy vào yêu cầu mong muốn, song có thể có hai vấn đề quan trọng đó là: thống kê mức xám của ảnh và tần số ảnh.

1.2.3.1. Lọc nhiễu

Nhiễu có nhiều loại nhưng có thể phân ra các loại nhiễu như: nhiễu do thiết bị thu nhận ảnh, nhiễu ngẫu nhiên độc lập, nhiễu do vật quan sát. Thường người ta xấp xỉ các loại nhiễu bằng các quá trình tuyến tính bất biến vì có nhiều công cụ tuyến tính có thể giải quyết vấn đề phôi phục ảnh cũng như tăng cường ảnh hơn so với phi tuyến và hơn nữa còn cho phép xử lý dễ dàng hơn trên máy tính.

Từ các vấn đề trên ta có thể làm trơn ảnh bằng việc lọc nhiễu theo các loại bộ lọc tuyến tính (Liner filter) hay lọc phi tuyến. Loại bộ lọc tuyến tính bao gồm như bộ lọc trung bình không gian (Mean filter, Average filter), lọc thông thấp (Low pass filter), Bộ lọc thông cao lý tưởng, Lọc Gaussian blur, vv… Loại bộ lọc phi tuyến bao gồm như Lọc trung vị (Median filter), Lọc giả trung vị, Lọc ngoài (Oulier filter), vv… Ở luận văn này tôi chỉ xin đề cập đến bộ lọc tuyến tính Gaussian blur như sau:

Theo tài liệu [5], Lọc Gaussian blurring là cách làm mờ một ảnh bằng hàm Gaussian. Phương pháp này được ứng dụng rộng rãi và hiệu quả trong các phần mềm xử lý đồ họa. Nó cũng là công cụ phổ biến để thực hiện quá trình tiền xử lý hình ảnh dùng để làm dữ liệu đầu vào tốt cho các phân tích cao cấp hơn trong thị giác máy tính (Computer vision), hoặc cho các giải thuật được thực hiện trong một tỉ lệ khác của hình đã được cho.

Như vậy, ta có thể nói Gaussian blurring là một loại bộ lọc làm mờ ảnh, sử dụng lý thuyết hàm Gaussian cũng được biết đến như là dạng phân tán chuẩn (Normal distribution) trong thống kê để tính toán việc chuyển đổi (Transformation) mỗi điểm ảnh của hình, giúp làm giảm nhiễu và mức độ chi tiết không mong muốn của hình ảnh. Sau đây là phương trình hàm Gaussian (Gaussion distribution) trong không gian hai chiều:

[ ] 1

m2 + n2

Gaussian m, n

= . exp (−

√2πσ

2σ2 ) (1.1)

Mặt nạ của bộ lọc này được xây dựng từ hàm Gaussian (1.6) trên. Mặt nạ Gaussian dạng hình vuông. Các hệ số của mặt nạ thường được tính giới hạn trong khoảng 4σ đến 6σ có thể cho ta hiệu quả cao.

1.2.3.1. Mức xám đồ

Mức xám đồ

Mức xám đồ của một ảnh xám là lược đồ biểu diễn tần suất xuất hiện của mỗi mức xám tức mức xám đồ của một hình ảnh là một hàm rời rạc. Lược đồ này được biểu diễn theo trục tọa độ (x,y). Trục hoành biểu diễn các mức xám từ 0 đến 255, còn trục tung biểu diễn số lượng điểm ảnh tương ứng với mức xám trên trục hoành.

Như vậy ta có mối quan hệ: y = f(x) = số điểm ảnh có cùng mức xám x.

Khi hàm được chuẩn hóa mà tổng của các mức xám là 1 thì hàm có thể được coi là một hàm mật độ. Đưa ra giá trị mức xám được tìm thấy trong ảnh. Theo đó thì giá trị mức xám là một giá trị ngẫu nhiên.

y = p(x) = h(x)

L − 1

với L thường bằng 256 (1.2)

Như vậy mức xám đồ cung cấp thông tin về mức xám của ảnh, nó là một công cụ hữu hiệu trong nhiều giai đoạn của quá trình xử lý ảnh.

Biến đổi mức xám đồ

Mức xám đồ biểu diễn cho một ảnh càng rộng càng tốt. Nếu coi x là giá trị mức xám của ảnh gốc và giá trị mức xám ảnh mới là:

s = T(x) với T được gọi là hàm biến đổi mức xám.

Một số biện pháp tăng cường ảnh bằng biến đổi mức xám đồ:

- San bằng mức xám đồ:

u

v = LTHĐ[f(u)] = LTHĐ [∑ p(x)] với 𝑥 = 0,1, … , 𝑢 (1.3)

x=0

Với p(x) là hàm mức xám đồ kiểu tỷ lệ, còn LTHĐ là phép lượng tử hóa đều giá trị của f(u) sang các giá trị mức xám từ 0 đến L-1. Sử dụng hàm lấy mẫu phần nguyên Int có thể có LTHĐ như sau:

LTHĐ[x] = Int [x − xmin (L − 1) + 0,5] với x = f(u) (1.4) 1 − xmin

- Biến đổi phi tuyến mức xám:

Trước khi thực hiện LTHĐ người ta sử dụng phi tuyến hàm f(u) biến đổi mức xám

u. Có thể có các dạng hàm f(u) như sau:

∑u [p(x)]1/n

f(u) =x=0

x=0

∑L−1[p(x)]1/n

với n là số nguyên > 1 (1.5)

f(u) = log(1 + u)

với u ≥ 0	(1.6)
f(u) = u1/n	với u ≥ 0 và n là số nguyên > 1	(1.7)

Có thể bạn quan tâm!

• Áp dụng độ đo entropy cho bài toán tách đặc trưng của bọt khí trên video và đề xuất kết hợp SVM cho vấn đề tự động theo dõi sục khí tại trạm quan trắc môi trường - 1
• Áp dụng độ đo entropy cho bài toán tách đặc trưng của bọt khí trên video và đề xuất kết hợp SVM cho vấn đề tự động theo dõi sục khí tại trạm quan trắc môi trường - 2
• Ví Dụ Về Các Hàm Thuộc Khác Nhau Số Tập Mờ Số Gần 2
• Nhận Dạng Và Nội Suy Ảnh (Image Recognition And Interpretation)
• Mô Hình Phân Lớp Ảnh Cho Bài Toán Nhận Dạng Bọt Khí

Xem toàn bộ 69 trang tài liệu này.

1.2.4. Phân tích và trích chọn đặc trưng ảnh (Image analysis and Feature extraction)

1.2.4.1. Giới thiệu chung về phân tích ảnh

Ảnh thu được sau khi được nâng cao sẽ cho ảnh trung thực hơn, rõ nét hơn. Nhưng các ảnh không đơn thuần chỉ là lưu trữ và hiển thị cho người xem, mà quá trình xử lý còn tiếp tục với ý nghĩa tự động tìm ra các thông tin chứa đựng trong ảnh đó để cung cấp cho nhu cầu của con người. Việc làm như vậy gọi là quá trình phân tích ảnh (Image analysis) hay còn gọi là biểu điễn và mô tả ảnh.

Phân tích ảnh là giai đoạn tiếp theo của tiền xử lý ảnh. Quá trình này biến đổi ảnh để từ đó đưa ra các đặc trưng quan trọng của ảnh. Đây là giai đoạn quan trọng nhất của quá trình xử lý ảnh. Trong một ảnh có thể có nhiều đối tượng, mỗi đối tượng mang những thông tin khác nhau, trong đó có những thông tin cần biết. Trong phân tích ảnh thường tìm các vùng đặc trưng điểm ảnh như biên ảnh (Boundary), vùng ảnh (Region), phân đoạn ảnh (Image segmentation) thành các vùng riêng biệt, vv… và biểu diễn lại thông qua các điểm ảnh đặc trưng. Phân tích ảnh mang hai ý nghĩa chính sau:

- Giảm bớt các thông tin không cần thiết trong ảnh, chỉ để lại những thông tin mang tính chất đặc trưng như là đường biên, khung xương, vv... của đối tượng.

- Phân tách các đối tượng trong ảnh ra một cách riêng rẽ nhau.

1.2.4.2. Tiêu chuẩn hoá và trích chọn đặc trưng ảnh

Tiêu chuẩn hoá (Normalization)

Sự biến đổi là thuộc tính cố hữu trong tự nhiên, và chính sự đa dạng về hình thức mà một bài toán nhận dạng còn tồn tại. Câu hỏi chính đặt ra cho bài toán nhận dạng là những biến đổi có thể giải quyết như thế nào? Có những đặc trưng của đối tượng là bất biến đối với tác động bên ngoài nên quá trình trích chọn đặc trưng có thể hoạt động được, nhưng cũng có những đặc trưng rất khó nắm bắt được khi đối tượng biến đổi. Chính vì vậy bước tiêu chuẩn hóa này thường có và cần thiết trong các bài toán nhận dạng. Nó thực hiện giảm bớt các thông số chịu ảnh hưởng nhiều của biến đổi, nói cách khác là việc thu nhỏ dữ liệu về một dạng chung mà ở dạng đó việc trích chọn các đặc trưng có thể được thực hiện đúng đắn.

Trích chọn đặc trưng (Feature extraction)

Trích chọn đặc trưng là bước biểu diễn các mẫu bằng các đặc trưng của đối tượng. Trong quá trình số liệu ảnh sẽ được thu gọn lại. Điều này hết sức cần thiết cho việc tiết kiệm bộ nhớ trong việc lưu trữ và thời gian tính toán. Nhiệm vụ đặt ra cho bước này là phải rút ra các thuộc tính đặc trưng riêng của đối tượng trong vùng ảnh. Sau đó mỗi đặc tính của đối tượng sẽ được mô tả dưới dạng số, các giá trị này tập hợp thành vector mô tả mẫu. Thực hiện nhiệm vụ này bao gồm hai công việc:

- Giảm nhỏ tập số liệu.

- Tập trung vào các số liệu đó để phân lớp các thông tin thiết yếu.

Việc trích chọn các đối tượng đặc trưng của đối tượng là việc lựa trọn ra các yếu tố hình học. Sự biến đổi từng yếu tố riêng có thể làm thay đổi trạt tự các đại lượng àm điều này có thể làm ảnh hưởng đến việc phân lớp. Vấn đề này thường được giải quyết bằng một phép biến đổi tuyến tính thích hợp đối với các thành phần của vector đặc trưng.

Một phương pháp trích chọn đặc trưng tốt nếu như nó trích cọn các đặc trưng của đối tượng mà các đặc trưng đó sẽ giúp cho việc phân biệt được các lớp mẫu khác nhau, đồng thời nó cũng biến đổi được các thuộc tính cố hữu của đối tượng hay do các thiết bị thu nhận ảnh tạo ra.

Cho đến nay thì chưa có một phương pháp toán học tối ưu nào để đáp ứng được yêu cầu trên. Các chuyên gia vẫn phải dựa vào trực giác và khả năng tưởng tượng để tìm ra đặc trưng thích hợp của đối tượng. Một số phương pháp lựa chọn điển hình như: phương pháp Morphology, phương pháp PCA [17], phương pháp tìm biên Canny [6], [16], [22], [23], phương pháp xác định độ đo Entropy[8], [20], vv…

1.2.4.3. Kỹ thuật tìm biên ảnh (Image boundary)

1.2.4.3.1. Khái quát về tìm biên

Biên của đối tượng ảnh:

Biên là nơi phân tách giữa hai vùng có mức xám tương đối khác nhau. Để xác định đối giới hạn của một đối tượng ảnh, người ta căn cứ vào đường biên của đối tượng ảnh. Biên của đối tượng cho biết khá nhiều thông tin đặc trưng của đối tượng vì vậy quá trình nhận dạng thượng dựa vào đường biên của đối tượng. Xét về mặt tín hiệu thì biên của ảnh tập hợp các điểm mà tại đó xác định một sự thay đổi đột ngột về cường độ sáng. Đây là cơ sở cho các kỹ thuật tìm biên.

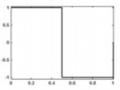
Một số kiểu đường biên hay gặp trong thực tế:

(a)

Biên dạng nhảy bậc

(b) Biên dốc

(c) Biên dạng xung vuông

(d) Biên dạng hình nón

Hình 1.2: Một số kiểu đường biên ảnh thông dụng

Phân loại kỹ thuật tìm biên:

Có hai phương pháp tìm biên cho đối tượng:

- Phương pháp trực tiếp: Sử dụng đạo hàm để tìm sự biến thiên của cường độ sáng. Ví dụ như kỹ thuật Gradient dùng đạo hàm bậc nhất, kỹ thuật Laplace dùng đạo hàm bậc

hai. Phương pháp này hiệu quả khi cường độ tại biên thay đổi đột ngột, ngoài ra nó ít chịu ảnh hưởng của nhiễu.

- Phương pháp gián tiếp: Thực hiện phân vùng ảnh trước và biên của vùng ảnh được phân tách ra chính là đường biên cần tìm. Phương pháp này hiệu quả đối với trường hợp sự thay đổi cường độ tại biên là nhỏ. Một số phương pháp phân vùng ảnh chính như: phân vùng ảnh dựa theo ngưỡng biên độ, phân vùng ảnh dựa theo miền đồng nhất, phân vùng ảnh dựa theo đường biên.

Theo [1], phương pháp phát hiện biên trực tiếp tỏ ra khá hiệu quả và ít chịu ảnh hưởng của nhiễu, song nếu sự biến thiên độ sáng không đột ngột, phương pháp tỏ ra kém hiệu quả, phương pháp phát hiện biên gián tiếp tuy khó cài đặt, song lại áp dụng khá tốt trong trường hợp này

Theo [6], các phương pháp phát hiện biên truyền thống thường dựa trên kết quả của phép tích chập (Convolution) giữa bức ảnh cần nghiên cứu f(x,y) và một bộ lọc 2D (Filter) h(x,y) thường được gọi là mặt nạ h (Mask).

+∞ +∞

h(x, y) ∗ f(x, y) = ∫ ∫ h(k1,k2)f(x − k1,, y − k2,)dk1,dk2

(1.8)

−∞ −∞

Nếu h(x,y) và f(x,y) có dạng rời rạc thì công thức (1.8) sẽ được viết lại thành:

+∞ +∞

h(n1, n2) ∗ f(n1, n2) = ∑ ∑ h(k1,k2)f(n1 − k1,, n2 − k2) (1.9)

k1=−∞ k2=−∞

Trên thực tế người ta hay dùng h(n, n) là ma trận [3*3 ] như sau:

h(−1,1) h(0,1) h(1,1)

h = [h(−1,1) h(0,1) h(1,1)]

h(−1,1) h(0,1) h(1,1)

Cấu trúc và giá trị của các toán tử phát hiện biên sẽ xác định hướng đặc trưng mà toán tử nhạy cảm với biên. Có một số toán tử thích hợp cho các đường biên có hướng nằm ngang, một số toán tử lại thích hợp cho việc tìm kiếm biên dạng thẳng đứng hay theo hướng đường chéo. Có nhiều phương pháp phát hiện biên đang được áp dụng, tuy nhiên ta có thể phân thành hai nhóm cơ bản là phát hiện biên dùng Gradient và phương pháp Laplacian. Ở luận văn này tôi chỉ xin giới thiệu với phương pháp Gradient như sau:

1.2.4.3.2. Kỹ thuật Gradient

Khái niệm Gradient:

Gradient là một vector có hai thành phần biểu thị tốc độ thay đổi giá trị cường độ sáng theo hai hướng x và y. Theo tài liệu [1], [6] và [23], nếu cho một ảnh liên tục f(x,y) thì hai thành phần của Gradient (ký hiệu: Gx, Gy) chính là đạo hàm riêng của f(x,y) theo hai hướng x và y như hai công thức (1.10 và 1.11) sau:

G = f

= ∂f(x, y) ≈ f(x + dx, y) − f(x, y)

(1.10)

x x ∂x dx

G = f

= ∂f(x, y) ≈ f(x, y + dy) − f(x, y)

(1.11)

y y ∂y dy

Trong đó dx, dy là khoảng cách tính theo hai hướng x và y. Trên thực tế, người ta hay dùng với dx = dy = 1.

Kỹ thuật Gradient:

Kỹ thuật này sử dụng một cặp mặt nạ h1 và h2 trực giao (theo 2 hướng vuông góc). Theo tài liệu [6], nếu định nghĩa Gx, Gy là gradient tương ứng theo 2 hướng x và y, thì biên độ của gradient ký hiệu là g tại điểm (m,n) được tính theo công thức (1.12):

𝐴0 = 𝑔(𝑚, 𝑛) = √𝐺2(𝑚, 𝑛) + 𝐺2(𝑚, 𝑛) (1.12)

𝑥 𝑦

Hướng của gradient vector được xác định theo công thức (1.13) sau:

𝜃 (𝑚, 𝑛) = 𝑡𝑎𝑛−1 (𝐺𝑥(𝑚, 𝑛)) (1.13)

𝑟 𝐺𝑦(𝑚, 𝑛)

Hướng của biên sẽ vuông góc với chiều của gradient vector này.

Ngoài ra các toán tử đạo hàm được áp dụng là khá nhiều, tiêu biểu như: toán tử Robert, Sobel, Prewitt, Sobel, Canny (dựa vào tính giá trị cực đại và cực tiểu của đạo hàm bậc nhất của ảnh) theo [6], [22], [23] và [25] như sau:

a) Toán tử Sobel:

Trên thực tế Sobel sử dụng hai mặt nạ có kích thước [3 * 3] trong đó một mặt nạ chỉ đơn giản là sự quay của mặt nạ kia đi một góc 900 như ở hình dưới. Các mặt nạ này được thiết kế để tìm ra các đường biên theo hướng dọc và hướng ngang một cách tốt nhất. Khi thực hiện phép tích chập (Convolution) giữa ảnh và các mặt nạ này ta nhận được các gradient theo hướng dọc và hướng ngang Gx, Gy. Toán tử Sobel có dạng như (hình 1.3) sau:

-1

-2	-1		-1	0	+1
0	0		0	-2	0	+2
+1	+2		+1	-1	0	+1

Hình 1.3: Cửa sổ mặt nạ dùng cho toán tử Sobel

b) Toán tử Prewitt

Phương pháp Prewitt gần giống với Sobel. Prewitt là phương pháp cổ điển nhất. Toán tử Prewitt được mô tả như (hình 1.4) sau:

-1

-1	-1		-1	0	+1
0	0		0	-1	0	+1
+1	+1		+1	-1	0	+1

Xem tất cả 69 trang.