Mô Hình Phân Lớp Ảnh Cho Bài Toán Nhận Dạng Bọt Khí

2.3. VẤN ĐỀ PHÂN LỚP CHO DỮ LIỆU ẢNH BỌT KHÍ

Phân lớp ở bài toán nhận dạng bọt khí này mục đích là phân tách ảnh vào thành 2 lớp riêng biệt là lớp ảnh có bọt khí và lớp ảnh không có bọt khí. Trong hệ thống nhận dạng bọt khí thì công việc quan trọng là xác định xem ảnh đưa vào có dạng bọt khí hay không. Khâu này rất quan trọng vì nó ảnh hưởng đến độ chính xác nhận dạng của toàn hệ thống. Ở đây việc lựa chọn tôi lựa chọn phương pháp phân lớp phù hợp là hết sức quan trọng để giải quyết phân lớp cho bài toán nhận dạng bọt khí này. Quá trình phân lớp sẽ được thực hiện theo 2 bước dưới đây:

2.3.1. Huấn luyện mô hình phân lớp dữ liệu ảnh

Chuẩn bị dữ liệu cho quá trình huấn luyện là các tập dữ liệu ảnh đã qua quá trình xử lý phân tích và trích chọn đặc trưng ở trước. Tập dữ liệu được đưa vào huấn luyện phân lớp. Sau khi kết thúc quá trình huấn luyện, hệ thống sẽ lưu lại giá trị các tham số này (các tham số quyết định phân lớp - mô hình sau khi huấn luyện) để phục vụ cho quá trình nhận dạng sau này. Quá trình huấn luyện dữ liệu nhanh hay chậm phụ thuộc vào số lượng mẫu dữ liệu tham gia huấn luyện, thuật toán chọn để huấn luyện dữ liệu.

2.3.2. Phân lớp dữ liệu ảnh – Thử nghiệm mô hình

Sau khi đã xây dựng xong mô hình huấn luyện dữ liệu ở bước 1 thì tiến hành phân lớp với một mẫu dữ liệu mới X. Dữ liệu X sẽ được thực hiện tiền xử lý, phân tích và trích chọn đặc trưng, sau đó được sẽ được đưa vào tính toán thông qua các tham số của hàm quyết định (các tham số của mô hình huấn luyện) để xác định lớp của mẫu dữ liệu X như hình sau:

Số hóa

Tiền xử lý

Dữ liệu huấn luyện

Dữ liệu nhận dạng

Huấn luyện Phân lớp

Trích chọn

đặc trưng

Mô hình sau khi huấn luyện

Nhận dạng

Kết quả nhận dạng

Hình 2.5: Mô hình phân lớp ảnh cho bài toán nhận dạng bọt khí

Bước phân lớp dữ liệu này gồm nhiều giai đoạn:

- Giai đoạn tiền xử lý ảnh:

Vì ảnh đầu vào (dữ liệu nhận dạng/ phân lớp) có thể có chứa nhiễu do ánh sáng, sóng trên mặt nước, màu nền không thích hợp, vv… nên dữ liệu này có thể được tiến hành tiền xử lý, phân tích và trích chọn đặc trưng trước khi nhận dạng.

- Giai đoạn trích chọn đặc trưng:

Để thực hiện quá trình phân lớp, bước trích chọn đặc trưng ảnh có vai trò rất quan trọng. Đặc trưng ảnh ở đây chính là đặc trưng nội dung ảnh, là phân tích nội dung thực sự của các frame ảnh. Nội dung ảnh được thể hiện bằng màu sắc, hình dạng, kết cấu (Texture), các đặc trưng cục bộ (Local features), vv... hay bất cứ thông tin nào có từ chính nội dung ảnh. Luận văn này sử dụng phương pháp trích chọn đặc trưng theo 2 hướng sử dụng phương pháp biến đổi Wavelet cho hướng trích chọn đặc trưng ảnh bằng việc kết hợp Entropy và Fuzzy Logic và phương pháp tìm biện như đã trình bày ở phần trên.

- Chọn thuật toán huấn luyện và phân lớp dữ liệu:

Sau khi hoàn thành giai đoạn trích chọn đặc trưng ảnh, tiếp theo là chọn thuật toán huấn luyện và phân lớp dữ liệu ảnh. Trong luận văn này là lựa chọn việc tiếp cận thuật toán học SVM cho huấn luyện và phân lớp dữ liệu sẽ được trình bày cụ thể ở phần phương pháp SVM cho bài toán nhận dạng bọt khí dưới đây.

2.4. PHƯƠNG PHÁP SVM CHO BÀI TOÁN NHẬN DẠNG BỌT KHÍ

2.4.1. Giới thiệu chung về SVM

Theo tài liệu [15], [16], [27] và [28], máy vector hỗ trợ (SVM: Support Vector Machines) là phương pháp phân loại rất hiệu quả được Vapnik giới thiệu năm 1995. Ý tưởng của phương pháp là cho trước một tập huấn luyện được biểu diễn trong không gian vector, trong đó mỗi một dữ liệu văn bản, một dữ liệu hình ảnh, vv… được xem như một điểm trong không gian này.

Phương pháp này tìm ra một siêu mặt phẳng (Optimal hyperplane) quyết định tốt nhất có thể chia các điểm trên không gian này thành các lớp riêng biệt. Chất lượng của siêu mặt phẳng này được quyết định bởi một khoảng cách (được gọi là biên) của điểm dữ liệu gần nhất của mỗi lớp đến mặt phẳng này. Khoảng cách biên càng lớn thì càng có sự phân chia tốt các điểm ra thành hai lớp, nghĩa là sẽ đạt được kết quả phân loại tốt. Mục tiêu của thuật toán SVM là tìm được khoảng cách biên lớn nhất để tạo kết qủa phân loại tốt.

Một máy vector hỗ trợ xây dựng một siêu phẳng hoặc một tập hợp các siêu phẳng trong một không gian nhiều chiều hoặc vô hạn chiều, có thể được sử dụng cho phân loại, hồi quy, hoặc các nhiệm vụ khác.

Một cách trực giác, để phân loại tốt nhất thì các siêu phẳng nằm ở càng xa các điểm dữ liệu của tất cả các lớp (gọi là hàm lề) càng tốt, vì nói chung lề càng lớn thì sai số tổng quát hóa của thuật toán phân loại càng bé.

Ví dụ về SVM tuyến tính:

Một không gian có nhiều điểm và các kí hiệu như hình (2.3) sau:

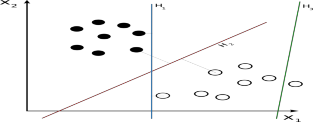
Hình 2.6: Mô tả 1 không gian nhiều điểm cho SVM tuyến tính Trong đó:

• yi: là các lớp (bản lề) chứa các điểm dữ liệu xi. Ở ví dụ này mang giá trị 1 và -1.

• xi: là một vector thực nhiều chiều.

Nhiệm vụ là cần phải tìm một siêu phẳng có lề lớn nhất chia tách các điểm dữ liệu có ban đầu để huấn luyện và các điểm sau này. Mỗi siêu phẳng đều có thể được viết dưới dạng một tập các điểm thỏa mãn: w.x - b = 0 (2.1)

Hình 2.7: Mô tả siêu phẳng cho SVM tuyến tính

Trong đó :

• w: là một vector pháp tuyến của siêu phẳng.

• Tham số b/||w|| : xác định khoảng cách giữa gốc tọa độ và siêu phẳng theo hướng vectơ pháp tuyến w.

Giả sử có tới 3 siêu phẳng là H1, H2, H3 như hình (2.6) trên thì H3 sẽ bị loại đầu tiên vì không thể phân loại các điểm huấn luyện cho trước. H1 bị loại vì khoảng cách từ các điểm vector hổ trợ đến siêu phẳng chưa phải là cực đại. H2 là siêu phẳng cần tìm. Lúc này các siêu phẳng đó được xác định:

w.x - b = 1 và w.x - b = -1 (2.2)

Các điểm dữ liệu cho trước nằm trên các siêu phẳng song song được gọi là vector hổ trợ (Support vector).

2.4.2. SVM cho bài toán 2 lớp

Giả sử có hai lớp khác nhau được mô tả bởi các điểm trong không gian nhiều chiều, hai lớp này là Linearly separable, tức tồn tại một siêu phẳng phân chia chính xác hai lớp đó.

Mục đích là tìm một siêu mặt phẳng phân chia hai lớp đó, tức tất cả các điểm thuộc một lớp nằm về cùng một phía của siêu mặt phẳng đó và ngược phía với toàn bộ các điểm thuộc lớp còn lại. Chúng ta đã biết rằng, thuật toán PLA (Perceptron Learning Algorithm) có thể làm được việc này nhưng nó có thể cho chúng ta vô số nghiệm như hình (2.8) dưới đây:

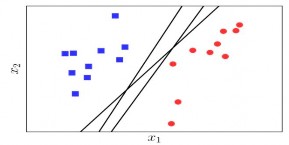
Hình 2.8: Các mặt phân cách hai lớp cho bài toán SVM 2 lớp

Vấn đề đặt ra ở đây là trong vô số các mặt phân chia ở trên, đâu là mặt phân chia tốt nhất theo một tiêu chuẩn nào đó? Trong ba đường thẳng minh họa trong hình (2.8) ở trên, có hai đường thẳng khá lệch về phía lớp có hình tròn đỏ. Điều này có thể khiến cho lớp màu đỏ không “thỏa” vì bị lấn chiếm nhiều.

Như vậy, cần xây dựng dựng một phương pháp để tìm được đường phân chia mà cả hai lớp đều cân bằng.

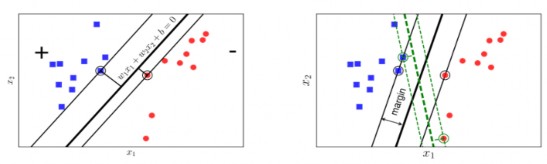
(a) (b)

Hình 2.9: Margin của hai lớp là bằng nhau và lớn nhất có thể

Nếu ta định nghĩa mức độ “thỏa” của một lớp chính là tỉ lệ thuận với khoảng cách gần nhất từ một điểm của lớp đó tới đường/mặt phân chia, khi đó ta nhận thấy:

- Xét hình 2.9(a): Lớp có hình tròn đỏ sẽ không được “thỏa” vì đường phân chia gần nó hơn so với lớp có hình vuông xanh rất nhiều. Do vậy, cần một đường phân chia sao cho khoảng cách từ điểm gần nhất của mỗi lớp tới đường phân chia là như nhau. Khoảng cách này được gọi là lề (Margin).

- Xét hình 2.9(b): Khi khoảng cách từ đường phân chia tới các điểm gần nhất của mỗi lớp là như nhau. Xét hai cách phân chia bởi đường nét liền màu đen và đường nét đứt màu xanh lục, đường nét liền màu đen chia hai lớp “thỏa” hơn bởi vì nó tạo ra một Margin rộng hơn.

Như vậy, việc Margin rộng hơn sẽ mang lại hiệu ứng phân lớp tốt hơn vì sự phân chia giữa hai lớp rạch ròi hơn. Đây là một điểm khá quan trọng giúp SVM mang lại kết quả

phân loại tốt hơn so với mạng neuron (Neural Network) với 1 layer (Perceptron Learning Algorithm).

Bài toán tối ưu trong SVM chính là bài toán đi tìm đường phân chia sao cho Margin là lớn nhất. Đây cũng là lý do vì sao SVM còn được gọi là Maximum Margin Classifier.

2.4.3. Xây dựng bài toán tối ưu cho SVM 2 lớp bọt khí

Sau khi nghiên cứu về một số phương pháp, thuật toán học máy như mạng neuron nhân tạo ANN (Artificial Neural Network) hay máy vector hổ trợ SVM (Support Vector Machine) và so sánh, tôi quyết định tiếp cận thuật toán học SVM và xây dựng bài toán tối ưu với 2 lớp ảnh như sau:

- Giả sử gọi bộ dữ liệu ảnh đưa vào phân lớp là (X,Y); với X=(x1,…xn) và

Y=(y1,…yn).

- Các cặp dữ liệu ảnh (điểm) biết trước: (x1,y1), (x2,y2),…, (xn,yn) ∈ X*Y gọi là tập dữ liệu huấn luyện (Training Data).

Với:

• Vector xi ∈ Rd: thể hiện đầu vào của một điểm dữ liệu ảnh (DataSet)

• Vector yi: là nhãn (Lable) của điểm dữ liệu đó

• d: là số chiều của dữ liệu

• n: là số điểm dữ liệu.

- Nhãn của mỗi điểm dữ liệu được xác định bởi yi=1 tương ứng với ảnh có bọt khí (Lớp 1) và yi=-1 tương ứng với ảnh không có bọt khí (Lớp 2).

Khi dữ liệu là phân tách tuyến tính, như một đường thẳng trên đồ thị của x1 và x2 phân tách hai lớp khi d = 2 và một siêu phẳng trên đồ thị của x1, x2… xT phân tách hai lớp với d>2.

Hình 2.10: Mô tả siêu phẳng cho SVM tuyến tính

Theo (2.1), siêu phẳng có thể được mô tả bởi phương trình: w.x - b = 0 và công việc sẽ được thực hiện tuần tự như sau:

1- Tìm đường biên thứ nhất (lớp1): w.x – b = 1 2- Tìm đường biên thứ hai (lớp2): w.x – b = -1

3- Tìm đường phân chia từ 2 đường biên và tính lề: Margin = 2/||w|| 4- Khử các lỗi.

2.4.4. Ưu điểm của SVM cho phân lớp ảnh bọt khí

SVM là phương pháp học có giám sát, có gán nhãn, thường dùng phân loại (Classification) đa lớp và được sử sụng rất nhiều trong phân loại. Khi huấn luyện phân lớp với dữ liệu biết trước và được gán nhãn đưa vào phân lớp dạng: (Data, Label).

Mặt khác, theo kết quả phân lớp lá cây trong [12], phân loại trong Tin sinh học [13], phân loại văn bản [14], có thể coi SVM là phương pháp phân lớp khá nhanh, có hiệu suất tổng hợp tốt và hiệu suất tính toán cao. SVM rất hiệu quả để giải quyết bài toán dữ liệu có số chiều lớn (như ảnh của dữ liệu biểu diễn gene, protein, tế bào, vv…). Đồng thời SVM cũng giải quyết vấn đề Overfitting rất tốt (dữ liệu có nhiễu và tách dời nhóm hoặc dữ liệu huấn luyện quá ít) như [12].

Như vậy, việc sử dụng SVM cho nghiên cứu này là nhằm xây dựng một siêu phẳng giữa hai lớp ảnh bọt khí và ảnh không bọt khí sao cho khoảng cách từ nó tới các điểm gần siêu phằng nhất của hai lớp là cực đại. Đường phân lớp tốt nhất chính là đường có khoảng cách lề (Margin) lớn nhất (tức là sẽ tồn tại rất nhiều đường phân cách xoay theo các phương khác nhau, và sẽ chọn ra được đường phân tách mà có khoảng cách lề là lớn nhất). Cụ thể ở luận văn này, SVM được sử dụng phân lớp trên ảnh đã trích chọn đặc trưng theo 2 hướng đã trình bày ở các phần trên như sau:

 Hướng 1: Để phân biệt sự khác nhau về độ lớn Entropy giữa các điểm ảnh thuộc và không thuộc khu vực có bọt khí. Sử dụng SVM để phân 2 lớp Có Bọt và Không Bọt.

 Hướng 2: Để phân biệt giữa ảnh có bọt và không bọt. Sử dụng SVM để phân 2 lớp Có Bọt và Không Bọt.

Chương 3: THỰC NGHIỆM VÀ ĐỀ XUẤT ỨNG DỤNG PHƯƠNG PHÁP TRÍCH CHỌN ĐẶC TRƯNG ẢNH CHO BÀI TOÁN NHẬN DẠNG ẢNH BỌT KHÍ

3.1. MÔI TRƯỜNG CÀI ĐẶT VÀ CÔNG CỤ SỬ DỤNG

Dựa vào cơ sở lý thuyết ở chương 1 và chương 2 ở trên, tôi xem xét và quyết định thực nghiệm trên môi trường cài đặt như sau:

- Ngôn ngữ lập trình Matlab.

- Cài đặt và chạy trên máy tính Dell Intel® Core™ ị-3320M CPU @2.60GHz, Ram 4.00GB.

3.2. DỮ LIỆU VÀ XÂY DỰNG TẬP DỮ LIỆU ẢNH BỌT KHÍ

Để thực nghiệm giải quyết vấn đề xử lý, phân tích trích chọn đặc trưng ảnh, tôi chuần bị 4 video clip từ 4 camera giám sát bể nuôi vi sinh, được trích xuất từ 4 trạm khác nhau vào các thời gian và không gian khác nhau (mỗi video clip tương ứng trên dưới 10.000 frame ảnh). Từ đó, với mỗi video clip của từng trạm sẽ được tách thành 2 tệp video clip khác nhau (một tệp là video clip tương ứng với trường hợp lúc bể có sục khí và một tệp là video clip với trường hợp lúc bể không được sục khí). Như vậy, tổng cộng có 8 tệp video clip đã được tách (4 tệp cho trường hợp có bọt khí tương ứng 4 trạm và 4 tệp cho trường hợp không có bọt khí tương ứng 4 trạm) để phục vụ cho việc xử lý, phân tích trích chọn đặc trưng ảnh trước khi chọn ảnh mẫu cho việc huấn luyện phân lớp.

Từ 8 tệp video clip ứng với 4 trạm đã tách trên, tôi tiến hành trích xuất các frame ảnh và chuyển đổi không gian màu sang mức xám (Image Gray).

Từ đó, thử nghiệm xử lý, phân tích trích chọn đặc trưng ảnh theo 2 hướng như đã trình bày ở chương 2 như sau:

- Hướng thứ nhất: Xác định giá trị Entropy cho các pixel (điểm ảnh) để xác định độ độ bất định các ảnh có các pixel ảnh có khả năng là ảnh có bọt khí hay không bọt khí cho từng tập ảnh (mỗi tập 100 ảnh) như đã trình bày ở chương 2. Sau đó sử dụng Fuzzy logic bằng việc dùng 1 hàm Activation để khử các những pixel ảnh không rõ ràng (trường hợp Entropy gần bằng 0). Đồng thời sử dụng phép biến đổi Wavelet Haar để thu gọn dữ liệu và kích thước ảnh về một dạng nhỏ mà tại đây vẫn hội đủ các thông tin quan trọng của các pixel ảnh ở các frame ảnh.

- Hướng thứ hai: Ứng dụng phương pháp và kỹ thuật dò biên ảnh Gradient (bằng việc sử dụng một số toán tử như: Roberts, Prewitt, Sobel, Canny) dựa vào tính giá trị cực đại và cực tiểu của đạo hàm bậc nhất của ảnh. Từ đó so sánh các kết quả và chọn ra phương pháp mang lại ảnh có chất lượng biên tốt nhất để phục vụ cho việc huấn luyện phân lớp mẫu và nhận dạng sau này.

3.3. ỨNG DỤNG ĐỘ ĐO ENTROPY KẾT HỢP FUZZY LOGIC VÀ WAVELET CHO TRÍCH CHỌN ĐẶC TRƯNG BỌT KHÍ

Từ 8 tệp video clip ứng với 4 trạm đã tách và chuyển đổi không gian màu sang mức xám như trình bày ở các phần trên, tôi tiến hành thử nghiệm xác định giá trị Entropy các pixel ảnh cho từng tập ảnh. Ở đây tôi chọn 1 tập là 100 ảnh vì lý do: cứ 1 giây camera đọc được khoảng 8 frame ảnh mà các con vi sinh sẽ chết vào khoảng 15 đến 16 giây nếu bể nuôi thiếu oxi. Như vây chọn 100 ảnh là vào khoảng 12 giây vừa đủ báo động cho trường hợp thiếu oxi (không được sục khí).

Sau cài đặt thực nghiệm trên Matlab, kết quả Entropy có được cho ảnh có bọt và không có bọt tương ứng như bảng (3.1) và bảng (3.2) dưới đây:

0	0	0	0	0	0	0	0	0	0	0
0.3685567775377070.0814620269150600 0 0									0	0	0
0.9078619154263700 0 0.4721893846767510									0	0	0
0	0	0.2885385136944100				0.1425733302598990.142573330259899
0	0	0 0 0 0				0 0 0

0	0	0	0	0	0	0	0	0	0
0	0	0	0	0	0	0	0	0	0	0	0
0	0	0	0	0	0	0	0	0	0	0	0
0	0	0	0	0	0	0	0	0	0	0	0
0	0	0	0	0	0	0	0	0	0	0	0
0.0244141642388290 0 0 0 0 0 0 0 0
0	0	0	0	0	0	0	0	0	0	0	0
0	0	0	0	0	0	0	0	0	0	0	0
0	0	0	0	0	0	0	0	0	0	0	0
0	0	0	0	0	0	0	0	0	0	0	0
0 0 0.0814620269150600 0 0 0 0 0 0
0	0	0	0	0	0	0	0	0	0	0	0
0	0	0	0	0	0	0	0	0	0	0	0
0	0	0	0	0	0	0	0	0	0	0	0
0	0	0	0	0	0	0	0	0	0	0	0
0	0	0	0	0	0	0	0	0	0	0	0
0	0	0	0	0	0	0	0	0	0	0	0
0	0	0	0	0	0	0	0	0	0	0	0
0	0	0	0	0	0	0	0	0	0	0	0
0	0	0	0	0	0	0	0	0	0	0	0
0	0	0	0	0	0	0	0	0	0	0	0
0	0	0	0	0	0	0	0	0	0	0	0
0	0	0	0	0	0	0	0	0	0	0	0
0	0	0	0	0	0	0.0814620269150600				0	0
0 …	0	0	0	0	0	0 0 0 0

0	0.142573330259899
0 0 0.3685567775377070 0 0	0	0 0 0
0 0.3685567775377070.5879303728017200	0	0 0

0	0	0	0.5610284863400680
0.8724752054851930	0	0	0	0 0 0 0	0