Trang chủ / Môi Trường

Ví Dụ Về Các Hàm Thuộc Khác Nhau Số Tập Mờ Số Gần 2

Hình 1.4: Cửa sổ mặt nạ dùng cho toán tử Prewitt

c) Toán tử Robert

Tương tự như Sobel, ta tính đường biên ngang và dọc một cách riêng rẽ dùng 2 mặt nạ như (hình 1.5) ở dưới, sau đó tổng hợp lại để cho ra đường biên thực của ảnh. Tuy nhiên do mặt nạ của Robert khá nhỏ nên kết quả là bị ảnh hưởng khá nhiều của nhiễu.


0

0

0


0

0

0

0

-1

0

0

0

-1

0

0

+1

0

+1

0

Có thể bạn quan tâm!

Xem toàn bộ 69 trang tài liệu này.

Áp dụng độ đo entropy cho bài toán tách đặc trưng của bọt khí trên video và đề xuất kết hợp SVM cho vấn đề tự động theo dõi sục khí tại trạm quan trắc môi trường - 4

Hình 1.5: Cửa sổ mặt nạ dùng cho toán tử Roberts

d) Toán tử Canny

Phương pháp này sử dụng hai mức ngưỡng cao và thấp. Ban đầu ta dùng mức ngưỡng cao để tìm điểm bắt đầu của biên, sau đó chúng ta xác định hướng phát triển của biên dựa vào các điểm ảnh liên tiếp có giá trị lớn hơn mức ngưỡng thấp. Ta chỉ loại bỏ các điểm có giá trị nhỏ hơn mức ngưỡng thấp. Các đường biên yếu sẽ được chọn nếu chúng được liên kết với các đường biên khỏe.

Phương pháp Canny có thể thực hiện theo 4 bước sau:

Bước 1. Dùng bộ lọc Gaussian (1.14) để làm mịn ảnh.

G′(x) = (− x ) e

σ2

−( x2 )

2

2σ


(1.14)

Bước 2. Tính toán gradient theo 2 công thức (1.15) và (1.16) dưới đây cho đường biên của ảnh đã được làm mịn. Vì đường biên trong ảnh là nơi phân cách giữa các đối tượng khác nhau, nên tại đó gradient của nó sẽ biến đổi mạnh mẽ nhất.

j x2+y2


C [x, y] = − (

x

σ2

i

) e−(

2σ2 ) (1.15)

x2+y2

y

C [x, y] = − (

σ2

) e−(

2σ2 ) (1.16)

Bước 3. Loại bỏ những điểm không phải là cực đại. Bước này sẽ tìm ra những điểm ảnh có khả năng là biên ảnh nhất bằng cách loại bỏ đi những giá trị không phải là cực đại trong bước tìm gradient ảnh ở trên.

Bước 4. Loại bỏ những giá trị nhỏ hơn mức ngưỡng. Vì nếu gradient tại một điểm trong ảnh có giá trị lớn hơn ngưỡng cao thì ta xác nhận đó là một điểm biên trong ảnh. Ngược lại, nếu giá trị này bé hơn ngưỡng thấp thì đó không phải điểm biên nên cần loại bỏ những giá trị này. Trường hợp giá trị gradient nằm giữa ngưỡng cao và ngưỡng thấp thì nó chỉ được tính là điểm trên biên khi các điểm liên kết bên cạnh của nó có giá trị gradient lớn hơn ngưỡng trên.

1.2.4.4. Độ đo Entropy

Trong tiếng việt chúng ta chưa có từ tương đương với từ Entropy, tuy nhiên có thể định nghĩa về mặt toán học như sau: Entropy là một đại lượng toán học dùng để đo lương thông tin không chắc chắn (hay lượng ngẫu nhiên) của một sự kiện hay của phân phối ngẫu nhiên cho trước. Hay một số tài liệu tiếng anh gọi là Uncertainty Measure.

Entropy của một sự kiện:

Theo tài liệu [8], giả sử có một sự kiện A có xác suất xuất hiện là p. Khi đó ta nói A có một đại lượng không chắc chắn được đo bởi hàm số h(p) với p ⊆ [0,1]. Hàm h(p) được gọi là Entropy nếu nó thõa mãn 2 tiêu đề toán học sau:

- Tiêu đề 1: h(p) là hàm liên tục không âm và đơn điệu giảm.

- Tiêu đề 2: Nếu A và B là 2 sự kiện độc lập nhau, có xác suất xuất hiện lần lượt là p(A) và p(B). Khi đó p(A,B) = pA.pB nhưng h(A,B) = h(pA)+h(pB).

Entropy của một phân phối:

Xét biến ngẫu nhiên X có phân phối:


X

x1 x2 x3 … xn

p

p1 p2 p3 … pn

Nếu Ai là sự kiện X=xi, (với i=1,2,3,…) thì Entropy của Ai là: h(Ai) = h(pi).

Gọi Y= h(X) là hàm ngẫu nhiên của X và nhận các giá trị là dãy các Entropy của các sự kiện X = xi, tức là Y = h(X) = {h(p1), h(p2),…, h(pn)}.

Như vậy, Entropy của X chính là kỳ vọng toán học của Y= h(X) có dạng:

H(X) = H(p1, p2, p3,…, pn) = p1h(p1) + p2h(p2) + … + pnh(pn) (1.17) Tổng quát là:

n

H(X) = ∑ pih(pi)

i=1


Định lý dạng giải tích của Entropy theo [8]: Hàm:


(1.18)

n

H(X) = H(p1, p2, … pn) = C ∑ pi log(pi) (1.19)

i=1

Trong đó:

• C: là 1 hằng số > 0

• n: là tổng số các giá trị có thể nhận

• i: là giá trị rời rạc thứ i


(bit).

• p(i): là xác suất xuất hiện của giá trị i

• Cơ số logarit là bất kỳ

• Bổ đề h(p) = -C.log(p)

• Trường hợp C =1 và cơ số logarit = 2 thì đơn vị tính là bit.

Khi đó h(p) = -log2(p), với đơn vị tính là bit và:

n

H(X) = H(p1, p2, … pn) = − ∑ pi log(pi) (1.20)

i=1

Quy ước trong cách viết là: log(pi) = log2(pi)

X

x1 x2 x3

p

½ ¼ ¼

Ví dụ: Nếu sự kiện A có xác suất xuất hiện là ½ thì h(A) = h(1/2) = -log(1/2) = 1 Giả sử biến ngẫu nhiên X có phân phối như sau:


1 , 1 , 1

) = −(

1

log (

1

) +

1

log (

1

) +

1

log (

1

) =

3

2 4 4


2


2


4


4


4


4


2

Lúc này Entropy sẽ là:


H(X)

= H (

(bit)


Theo tài liệu [20] của Claude Shannon thì tác giả xây dựng định nghĩa về Entropy để thõa mãn các giả định sau:

- Entropy phải tỷ lệ thuận liên tục với các xác suất xuất hiện của các phần tử ngẫu nhiên. Thay đổi nhỏ trong xác suất phải dẫn đến thay đổi nhỏ trong Entropy.

- Nếu các phần tử ngẫu nhiên đều có xác suất xuất hiện bằng nhau, việc tăng số lượng phần tử ngẫu nhiên phải làm tăng Entropy.

- Có thể tạo các chuỗi tín hiệu theo nhiều bước và Entropy tổng cộng phải bằng tổng số trọng số của Entropy của từng bước.

Shannon cũng chỉ ra rằng, bất cứ định nghĩa nào của Entropy cho 1 tín hiệu có thể nhận các giá trị rời rạc thõa mãn các giả định của ông thì đều có dạng:

n

−C ∑ pi log(pi) (1.21)

i=1

Như vậy, có thể gọi Entropy là đại lượng đo thông tin (hay còn gọi là độ bất định).

Nó được tính như một hàm phân bố xác suất.

Giả sử ta có một biến ngẫu nhiên X nhận các giá trị trên một tập hữu hạn theo một phân bố xác suất p(X). Thông tin thu nhận được bởi một sự kiện xảy ra tuân theo một phân

bố p(X) là gì?. Tương tự, nếu sự kiện còn chưa xảy ra thì cái gì là độ bất định và kết quả?. Đại lượng này được gọi là Entropy của X và được kí hiệu là H(X).

Ví dụ 1: Giả sử biến ngẫu nhiên X biểu thị phép tung đồng xu. Phân bố xác suất là: p(mặt xấp)= p(mặt ngữa)= 1/2. Có thể nói rằng, thông tin (hay Entropy) của phép tung đồng xu là một bit vì ta có thể mã hoá mặt xấp bằng 1 và mặt ngữa bằng 0. Tương tự Entropy của n phép tung đồng tiền có thể mã hoá bằng một xâu bít có độ dài n.

Ví dụ 2: Giả sử ta có một biến ngẫu nhiên X có 3 giá trị có thể là x1, x2, x3 với xác suất tương ứng bằng 1/2, 1/4, 1/4. Cách mã hiệu quả nhất của 3 biến cố này là mã hoá x1 là 0, mã của x2 là 10 và mã của x3 là 11. Khi đó số bít trung bình trong phép mã hoá này là:

1/2 1 +1/4 2 + 1/4 2 = 3/2

Các ví dụ trên cho thấy rằng, một biến cố xảy ra với xác suất 2-n có thể mã hoá được bằng một xâu bít có độ dài n. Tổng quát hơn, có thể coi rằng, một biến cố xảy ra với xác suất p có thể mã hoá bằng một xâu bít có độ dài xấp xỉ -log2 p. Nếu cho trước phân bố xác suất tuỳ ý p1, p2,. . ., pn của biến ngẫu nhiên X, khi đó độ đo thông tin là trọng số trung bình của các lượng -log2pi.

Điều này dẫn tới định nghĩa hình thức hoá như sau: Giả sử X là một biến ngẫu nhiên lấy các giá trị trên một tập hữu hạn theo phân bố xác suất p(X). Khi đó Entropy của phân bố xác suất này được định nghĩa là lượng:

n

H(X) = − ∑ pi log2(pi) (1.22)

i=1

Nếu các giá trị có thể của X là xi ,1 i n thì ta có:

n

H(X) = − ∑ p(X = xi) log2 p(X = xi) (1.23)

i=1

Nhận xét:

Nhận thấy rằng, log2 pi không xác định nếu pi = 0. Bởi vậy đôi khi Entropy được định nghĩa là tổng tương ứng trên tất cả các xác suất khác 0. Vì limx0 x log2x = 0 nên trên thực tế cũng không có trở ngại gì nếu cho pi = 0 với giá trị i nào đó. Tuy nhiên ta sẽ tuân theo giả định là khi tính Entropy của một phân bố xác suất pi , tổng trên sẽ được lấy trên các chỉ số i sao cho pi 0. Ta cũng thấy rằng việc chọn cơ số của logarit là tuỳ ý, cơ số này không nhất thiết phải là 2. Một cơ số khác sẽ chỉ làm thay đổi giá trị của Entropy đi một hằng số.

Chú ý rằng, nếu pi = 1/n với 1 i n thì H(X) = log2n. Cũng dễ dàng thấy rằng H(X) 0 và H(X)= 0 khi và chỉ khi pi = 1 với một giá trị i nào đó và pj = 0 với mọi j i.

Xét Entropy của các thành phần khác nhau của một hệ mật. Ta có thể coi khoá là một biến ngẫu nhiên K nhận các giá trị tuân theo phân bố xác suất pK và bởi vậy có thể tính được H(K). Tương tự ta có thể tính các Entropy H(P) hay H(C) theo các phân bố xác suất tương ứng của bản mã và bản rõ.

Ví dụ 3: Từ ví dụ 2 ở trên ta có thể tính được H(P) như sau:

H(P) = -1/4log21/4 - 3/4log23/4 = -1/4(-2) - 3/4(log23-2) = 2 - 3/4log23 0,81 Với các tính toán tương tự, ta sẽ có được H(K) = 1,5 và H(C) 1,85.

1.2.4.5. Fuzzy Logic


Tập mờ:

Các tập mờ được xác định bởi hàm thuộc mà các giá trị của nó là các số thực từ 0 đến 1. Chẳng hạn tập mờ những người thoả mãn tính chất người trẻ (chúng ta sẽ gọi là tập mờ người trẻ) được xác định bởi hàm thu ộc nhận giá trị 1 trên tất cả những người dưới 30 tuổi, nhận giá trị 0 trên tất cả những người trên 60 tuổi và nhận giá trị giảm dần từ 1 tới 0 trên các tuổi từ 30 đến 60.

Nguoitre = {1/0, 1/10, 1/20, 1/30, 0.75/40, 0.5/50, 0.25/60, 0/70, 0/80, 0/90, 0/100}

Theo tài liệu [9], một tập mờ A trong vũ trụ U được xác định là một hàm µA: U → [0,1]. Hàm µA được gọi là hàm thuộc (hàm đặc trưng) của tập mờ A còn µA(x) được gọi là mức độ thuộc của x vào tập mờ A. Như vậy tập mờ là sự tổng quát hoá tập rõ bằng cách cho phép hàm thuộc lấy giá trị bất kỳ trong khoảng [0,1], trong khi hàm thuộc của tập rõ chỉ lấy hai giá trị 0 hoặc 1.

Tập mờ A trong vũ trụ U được biểu diễn bằng tập tất cả các cặp phần tử và mức độ thuộc của nó:

A = {(x, µA(x)) | x ∈ U} (1.24)

Ví dụ 1: Giả sử các điểm thi được cho từ 0 đến 10, U = {0, 1, …, 10}. Chúng ta xác định ba tập mờ A = “điểm kém”, B = “điểm trung bình”, C = “điểm khá” bằng cách cho mức độ thuộc của các điểm vào mỗi tập mờ như bảng sau:


Điểm

A

B

C

0

1

0

0

1

1

0

0

2

1

0.25

0

3

0.75

0.5

0

4

0.5

0.75

0

5

0.25

1

0.25

6

0

0.75

0.5

7

0

0.5

0.75

8

0

0.25

1

9

0

0

1

10

0

0

1

Bảng 1.1: Ví dụ về các tập mờ điểm thi cho A, B, C


Một số ký hiệu truyền thống của tập mờ:

- Theo tài liệu [9], nếu vũ trụ U là rời rạc và hữu hạn thì tập mờ A trong vũ trụ U được biểu diễn như sau:

A = ∑ µA

x

(1.25)

x∈U

Ví dụ 2: Giả sử U ={a, b, c, d, e}, ta có thể xác định một tập mờ A như sau:

A = 0.7 0 0.3


1 0.5


a + b +

c + d + e

Ví dụ 3: Giả sử tuổi của người là từ 0 đến 100. Tập mờ A = “tuổi trẻ” có thể xác định như sau:


25 100

1


(1 + (

−1

y − 25

5 ))

A = ∑ y + ∑ y

y=0 y=25

Đó là một cách biểu diễn củ tập mờ có hàm thuộc là:

1 0 ≤ y ≤ 25

y − 25 2 −1

µA(y) =

(1 + (

{

5 ) )

25 ≤ y ≤ 100

- Cũng theo [9], khi vũ trụ U là liên tục, người ta sử dụng cách viết sau để biểu diễn tập mờ A như sau:

A = ∫ µA(x)/x (1.26)

U

Trong đó, dấu tích phân (cũng như dấu tổng ở trên) không có nghĩa là tích phân mà để chỉ tập hợp tất cả các phần tử x được gắn với mức độ thuộc của chính nó

Ví dụ 4: Tập mờ A = “số gần 2” có thể được xác định bởi hàm thuộc như bên dưới:

−∞

A

µ (x) = e−(x−2)2 , chúng ta viết A = ∫∞

e−(x−2)2 /x

Cần chú ý rằng, hàm thuộc đặc trưng cho tập mờ số gần 2 có thể được xác định bằng cách khác, chẳng hạn:


µA(x) =

0 x < 1

x − 1 1 ≤ x < 2

1 x = 2

−x + 3 2 < x ≤ 3

{ 0 x > 3


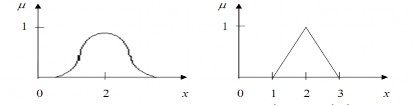
Hình 1 6 Ví dụ về các hàm thuộc khác nhau số tập mờ số gần 2 Các tập mờ 1

Hình 1.6: Ví dụ về các hàm thuộc khác nhau số tập mờ số gần 2

Các tập mờ được sử dụng rộng rãi trong các ứng dụng là các tập mờ trên đường thẳng thực R và các tập mờ trong không gian Ơclit n chiều Rn(n≥ 2).

Ví dụ 5: Giả sử tốc độ của một chuyển động có thể lấy giá trị từ 0 với νmax = 150 (km/h). Chúng ta có thể xác định 3 tập mờ “tốc độ chậm”, “tốc độ trung bình”, “tốc độ nhanh” như trong hình:

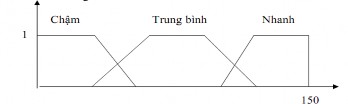
Hình 1 7 Ví dụ các tập mờ tốc độ chậm tốc độ trung bình tốc độ nhanh 2

Hình 1.7: Ví dụ các tập mờ tốc độ chậm, tốc độ trung bình, tốc độ nhanh.

Các tập mờ này được gọi là các tập mờ hình thang, vì hàm thuộc của chúng có dạng hình thang.

Thông thường khi thiết kế một tập mờ người ta thường sử dụng các dạng hình học của nó, theo tài liệu [9] và [10] có 3 dạng hình học khi thiết kế tập mờ là: tập mờ hình tam giác, hình thang, hình chuông.

Ví dụ 6: Tập mờ hình tam giác

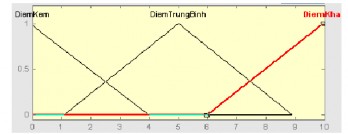
Hình 1 8 Ví dụ các tập mờ ở dạng hình tam giác Từ dạng hình tam giác trên ta 3

Hình 1.8: Ví dụ các tập mờ ở dạng hình tam giác

Từ dạng hình tam giác trên ta xác định được các tập mờ A, B, C như sau:


Điểm

A

B

C

0

1

0

0

1

0.75

0

0

2

0.5

0.25

0

3

0.25

0.5

0

4

0

0.75

0

5

0

1

0

6

0

0.75

0.25

7

0

0.5

0.5

8

0

0.25

0.75

9

0

0

0.25

10

0

0

1

Bảng 1.2: Ví dụ minh họa các tập mờ điểm thi cho A, B, C dạng tam giác

Trong thực tế, đặc biệt là khi lập trình ứng dụng ta thường biểu diễn tập mờ bằng một cấu trúc mảng.

Ví dụ 7:

U = [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10]

C = [1, 0.75, 0.5, 0.25, 0, 0, 0, 0, 0, 0, 0]

B = [0, 0, 0.25, 0.5, 0.75, 1, 0.75, 0.5, 0.25, 0,0]

A = [0, 0, 0, 0, 0, 0, 0, 0.25, 0.5, 0.75, 1]

Nhận xét:

Các tập mờ được đưa để biểu diễn các tính chất không chính xác, không rõ ràng, mờ, chẳng hạn các tính chất “người già”, “số gần 2”, “nhiệt độ thấp”, “áp suất cao”, “tốc độ nhanh”, vv...

Khái niệm tập mờ là một khái niệm toán học hoàn toàn chính xác. Một tập mờ trong vũ trụ U là một hàm xác định trên U và nhận giá trị trong đoạn [0,1]. Các tập rõ là tập mờ, hàm thuộc của tập rõ chỉ nhận giá trị 0, 1. Khái niệm tập mờ là sự tổng quát hoá khái niệm tập rõ.

Một tính chất mờ có thể mô tả các tập mờ khác nhau, trong các ứng dụng ta cần xác định các tập mờ biểu diễn các tính chất mờ sao cho phù hợp với thực tế, với các số liệu thực nghiệm.

Hàm Activation:

( ) 𝟏

𝟏 + 𝒆∝𝒙


𝐟 ∝, 𝐱

= ∝ . 𝒍𝒐𝒈𝟏𝟎 (𝟏 + 𝒆∝(𝒙−𝟏)) (1.27)

Hàm Activation là một hàm phi tuyến, thường được dùng trong mạng nơron 2 lớp, có thể được chứng minh là một xấp xỉ hàm phổ quát. Hàm trên thể hiện một đường dốc phụ thuộc tham số ∝. Các hệ số ở hàm trên là phi tuyến nên để độ dốc là tuyến tính cần phải xấp xỉ từ nhiều hàm phi tuyến


1.2.4.6. Phép biến đổi Wavelet


Biến đổi Wavelet liên tục thuận:

Theo [19], [21]. phương pháp Wavelet liên tục thuận có thể hiểu như sau:

Gọi f(x) là tín hiệu 1-D, phép biến đổi wavelet liên tục của f(x) sử dụng hàm wavelet ψ0 được biểu diễn bởi:

𝑊(s, b) = 1

∞

𝑥 − 𝑏

∫ 𝑓(𝑥) ψ∗ ( ) 𝑑𝑥 (1.28)


Trong đó:


√𝑠

−∞

0 𝑠

..... Xem trang tiếp theo?
⇦ Trang trước - Trang tiếp theo ⇨

Ngày đăng: 13/03/2023