Hình 1.17 – Hình ảnh nhóm 6 cọc bị gãy (Kok, 2009)
![]() Nhận xét:
Nhận xét:
Tổng hợp từ các nghiên cứu trên thì các nguyên nhân chính gây ra sự cố cọc bên trong hố đào là do:
- Tiến hành đào trước khi lắp đặt hệ chống đỡ.
- Lựa chọn hệ thống tường chắn không phù hợp để khống chế chuyển vị của đất.
- Không xét tới tải thi công trên công trường.
- Thiết kế cọc không xét tới ảnh hưởng của tải trọng ngang do quá trình thi công.
- Cốt thép trong cọc không đủ để chống chuyển vị của đất.
- Lớp đất sét yếu quá dày.
Ngoài ra, vị trí moment uốn lớn nhất trong cọc là tại mặt tiếp giáp giữa lớp đất yếu và đất tốt.
Chương 2: CƠ SỞ LÝ THUYẾT
Một số phương pháp được sử dụng giải quyết bài toán địa kỹ thuật là: Phương pháp thực nghiệm, phương pháp cân bằng giới hạn và phương pháp số. Phương pháp số bao gồm các phương pháp sai phân hữu hạn, phương pháp phần tử biên và phương pháp phần tử hữu hạn (PTHH). Phương pháp phân tử hữu hạn là một công cụ hữu ích để giải quyết bài toán về sự tương tác của cấu tạo đất như thiết kế hố đào và nền móng. Sử dụng phương pháp phần tử hữu hạn thích hợp hơn các phương pháp khác bởi vì:
Phương pháp PTHH có khả năng phân tích bài toán 2 chiều và 3 chiều.
Phương pháp PTHH có thể kết hợp dễ dàng ứng xử phi tuyến của đất.
Phương pháp phần tử hữu hạn có nhiều ứng dụng, với nhiều gói phần mềm với công cụ phương pháp phần tử hữu hạn như: Abaqus, ACTRAN, ADNIA, FLAC và Plaxis…
2.1. Phân tích phần tử hữu hạn trong PLAXIS
Sự phát triển của phần mềm phần tử hữu hạn có tính thương mại trong phân tích địa kỹ thuật được bắt đầu vào cuối những năm 80, và ngày nay đã phổ biến rộng rãi. Có nhiều cách khác nhau để ứng dụng phần tử hữu hạn vào các ngành kỹ thuật khác nhau, và vấn đề phân tích bài toán địa kỹ thuật cũng có những đặc trưng riêng và thường rất phức tạp (Potts, 2002).
Trong chương này sẽ giới thiệu về phần mềm Plaxis 3D Foundation. Nó cũng bao gồm giới thiệu cách thức tạo mô hình, sau đó sẽ đi tìm các đặc trưng trong Plaxis 3D foundation của vật liệu.
2.1.1. PLAXIS 3D Foundation
Plaxis được nghiên cứu tại Đại học Delft vào năm 1987, là phần mềm sử dụng phương pháp phần tử hữu hạn để phân tích khu vực ven sông ở Hà Lan. Mãi đến năm 2001 mới có mô hình 2D và khi đó PLAXIS 3D Tunnel đã được phát hành. Ba năm sau, PLAXIS 3D Foundation được tạo ra, nó được phát tiển nhằm phục vụ tính toán nền móng công trình và dùng trong ngành địa kỹ thuật như tính toán ổn định, độ lún và biến dạng.
Khi nói rằng chuyển từ phân tích 2D sang 3D rất khả thi nhưng đồng thời sự phức tạp cũng tăng lên. Điều này cũng chính là tăng khối lượng tính toán. Nếu một tính toán chi tiết chỉ mất vài phút để thực hiện trong phân tích 2D, nhưng tính toán tương tự trong phân tích 3D có thể mất hàng giờ. Mô hình phân tích ảnh hưởng của các giai đoạn thi công hố đào đến cọc bên trong hố đào cũng là một trong các trường hợp đó. PLAXIS 3D Foundation gồm ba phần chính, đó là mô hình (model), tính toán (calculation) và xuất kết quả (Output).
2.1.2. Mô hình
Trong chế độ mô hình thì hình dạng của mô hình được xây dựng. Biên của các lớp đất và đặc trưng vật liệu được thiết lập. Xây dựng các phần tử như tường và dầm tại các vị trí trong mô hình và đặc trưng tiếp xúc được định nghĩa. Cuối cùng lưới được tạo ra và đạt một độ mịn thích hợp. Trong đó việc lựa chọn mô hình đất là rất quan trọng, và sẽ được trình bày trong phần sau.
2.1.3. Tính toán
Trong chế độ tính toán, một số bước tính toán có thể được tạo ra. Khác nhau trường hợp tải và hình dạng được thiết lập để mô phỏng trình tự xây dựng công trình thực tế. Đối với mỗi bước có thể thiết lập các điều kiện mực nước ngầm khác nhau, các bộ phận công trình có thể được kích hoạt. Hố đào được mô phỏng bằng cách chấm dứt hoạt động của các tập hợp. Các loại tính toán phải được định nghĩa có thể là tính dẻo (Plastic) hoặc cố kết (consolidation). Phân tích cố kết (consolidation) được sử dụng khi mô hình các ứng xử phụ thuộc vào thời gian như sự phát triển và tiêu tán áp lực nước lỗ rỗng hay khi yêu cầu tính toán độ lún do từ biến. Tính toán tích dẻo (Plastic) được dùng để phân tích biến dạng đàn – dẻo (elastic-plastic) theo lý thuyết biến dạng nhỏ (Brinkgreve, 2007). Ứng suất và biến dạng được tính toán cho tất cả các nút còn trong trạng thái giới hạn.
2.1.4. Xuất kết quả
Trong phần chính thứ ba của Plaxis là chế độ xuất kết quả tính toán và được dùng xử lý kết quả tính toán. Biến dạng, ứng xuất và áp lực nước lỗ rỗng sẽ được
thể hiện trong mỗi bước tính toán, còn đối với các cấu kiện công trình ta có thể xem được moment uốn và lực cắt.
2.2. Tạo mô hình
Để phân tích phần tử hữu hạn trên phần mềm PLAXIS 3D Foundation thì điều quan trọng đầu tiên là phải tạo mô hình hình học cho bài toán. Mô hình này mô tả cấu trúc của công trình trong không gian 3 chiều được chương trình định nghĩa thông qua các mặt phẳng làm việc và các hình trụ hố khoan địa chất. Mô hình bao gồm các lớp địa tầng, kết cấu của công trình và các loại tải trọng. Mô hình phải đủ lớn để biên bài toán không ảnh hưởng đến kết quả phân tích.
Mặt phẳng làm việc (Work Planes): là các mặt phẳng nằm ngang theo trục x - z tương ứng với một cao độ y.
Điểm và đường thẳng (Geometry line): dùng để tạo mô hình hình học cho bài toán.
Phần tử dầm (Beam): dùng để mô hình cho kết cấu thanh mảnh chịu uốn và lực dọc trục như dầm móng…
Phần tử sàn (Floor): dùng mô phỏng cho kết cấu có chiều dày nhỏ theo phương ngang và chịu uốn như bản móng…
Phần tử tường (Wall): dùng mô hình cho kết cấu có chiều dày nhỏ theo phương đứng và chịu uốn như vách tầng hầm…
Phần tử cọc (Pile): dùng mô hình cho các loại cọc.
Phần tử lò xo (Spring): dùng để gắn kết vào một mặt của kết cấu và khống chế mặt đó so với mặt khác. Phần tử này thường dùng mô phỏng sự làm việc của cọc đơn.
Phần tử biên (Line Fixity): dùng để tạo biên khống chế cho bài toán.
Phần tử hố khoan (Borehole): dùng khai báo các lớp địa chất cho bài toán.
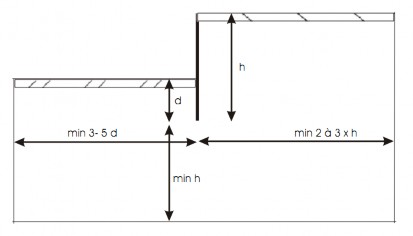
Hình 2.1 – Yêu cầu tối thiểu của mô hình hố đào (Bakker, 2005)[5]
2.3. Chia lưới phần tử
Để thực hiện tính toán phần tử hữu hạn,mô hình hình học trong PLAXIS 3D Foundation phải được chia thành các phần tử nhỏ hơn, được gọi là chia lưới phần tử hữu hạn. Mỗi phần tử bao gồm một số lượng nhất định các nút hình thành hệ thống phương trình cho việc tính toán. Số lượng các nút nhiều sẽ kéo theo hệ thống phương trình lớn hơn để máy tính giải quyết . Trong 2D mỗi nút có hai bậc tự do, tức là các nút có thể di chuyển theo phương x và y, xem Hình 4.2
Phần tử
Nút
Hình 2.2 – Các phần tử và nút trong một mô hình 2D. Mỗi nút có hai bậc tự do, được mô tả bởi các mũi tên trong hình nhỏ hơn, (Wiberg, 1974)[4]
Khi mô hình trong không gian ba chiều, mỗi nút có ba bậc tự do, kết quả là sẽ cho một hệ thống phương trình lớn hơn vì thực tế rằng mỗi nút cũng có thể di chuyển theo phương z.
Phân tích phần tử hữu hạn sẽ tiến hành theo ba bước, xem hình 2.3. Bước đầu tiên là phân chia mô hình thành các phần nhỏ hơn bằng cách tạo ra các phần tử (Generate elements) vào mô hình, trong đó mỗi phần tử tương đối dễ để giải từng cái một. Bước tiếp theo là phân tích các phần tử (Element analysis). Bước cuối cùng là phân tích hệ thống (System analysis) nơi mà tất cả các phần tử được kết nối với một hệ thống bằng các điều kiện biên, (Wiberg, 1974).
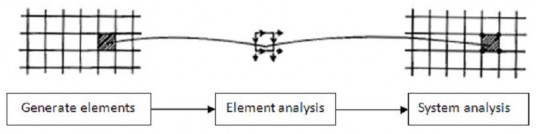
Hình 2.3 – Các bước phân tích phần tử hữu hạn (Wiberg, 1974)[4]
Phân tích phần tử hữu hạn là một phương pháp tính gần đúng và nguồn lỗi nhiều và thường không thể tránh khỏi (Wiberg, 1974). Số lượng nút trong mô hình có tác động đáng kể đến kết quả tính toán. Số lượng phần tử lớn hơn tạo ra một số lượng lớn các nút cho kết quả chính xác hơn mô hình có ít nút. Khi thiết kế các mô hình phức tạp thì thích hợp có số nút cao hơn so với trường hợp đơn giản hơn.
Các thiết lập mặc định cho kích thước cluster trong PLAXIS 3D Foundation là lưới thô (Coarse mesh). Chia lưới thế này có thể đủ kích thước khi mô hình các trường hợp đơn giản và tính chính xác của tính toán không cần cao. Hệ thống phương trình dễ dàng hơn cho máy tính để giải quyết và thời gian tính toán tương đối ngắn.
Nếu cần độ chính xác cao hơn thì cần sự làm mịn các cluster. Nếu toàn bộ mô hình cần được làm mịn, thì sử dụng chức năng Global coarseness để thay đổi kích thước phần tử cả phương đứng và ngang với khoảng từ rất thô (Very coarse) đến rất mịn (Very fine). Lưu ý rằng nếu chúng ta chia lưới 2D quá mịn sẽ làm tăng phần tử khi tiến hành chia lưới 3D và đồng nghĩa là thời gian tính toán sẽ tăng lên.
Số lượng nút và chuyển vị
Tổng chuyển vị (mm)
Để xác định mô hình gồm bao nhiêu nút là đủ, Hannes và Daniel (2010) đã thực hiện mô phỏng với số lượng các nút là tăng dần dần trên cùng một mô hình. Kết quả được so sánh với chuyển vị, xem hình 2.4.
Hình 2.4 – Kết quả chuyển vị với số nút tăng dần trong mô hình 3D, (Hannes và Daniel, 2010) [4]
2.4. Mô hình ứng xử của đất
2.4.1. Mô hình Mohr – Coulumb (MC)
Mô hình Mohr-Coulomb trong Plaxis được dựa trên ý tưởng của quy luật cơ bản đàn - dẻo với mặt ngưỡng cố định không bị tác động bởi biến dạng dẻo và trạng thái ứng suất của một điểm nằm trong mặt ngưỡng là đàn hồi thuần túy.
Không có quy luật tái bền hay hóa mềm yêu cầu đối với mô hình Mohr- Coulomb vì nó được giả dịnh là dẻo thuần túy. Hàm ngưỡng dẻo, f , được giới thiệu như là một hàm ứng suất và biến dạng mà có thể được trình bày như là một mặt trong không gian ứng suất chính. Mô hình Mohr – Coulumb yêu cầu 5 thông số cơ bản, xem Bảng 4.1.
Bảng 2.1 – Đặc trưng vật liệu đất trong mô hình Mohr – Coulumb
Đơn vị | Định nghĩa | |
E, Mô đun Young | kN/m2 | Mô đun đàn hồicủa đất |
, Hệ số poisson | - | Sự thay đổi ứng suất vuông góc với hướng tải tác dụng |
, Góc ma sát | ° | Góc nội ma sát của đất |
c, Lực dính | kN/m2 | Sức hút của các phân tử đất hạt mịn |
, Góc giãn nở | ° | Sự thay đổi thể tích của đất trong suốt quá trình cắt |
Có thể bạn quan tâm!
-
 Ảnh hưởng của hố đào sâu nền đất yếu tới cọc chống - 1
Ảnh hưởng của hố đào sâu nền đất yếu tới cọc chống - 1 -
 Ảnh hưởng của hố đào sâu nền đất yếu tới cọc chống - 2
Ảnh hưởng của hố đào sâu nền đất yếu tới cọc chống - 2 -
 Toàn Cảnh Hố Đào – Công Trình 15 Tầng, Quận 8, Tp. Hồ Chí Minh
Toàn Cảnh Hố Đào – Công Trình 15 Tầng, Quận 8, Tp. Hồ Chí Minh -
 Đặc Trưng Vật Liệu Đất Trong Mô Hình Hardening Soil
Đặc Trưng Vật Liệu Đất Trong Mô Hình Hardening Soil -
 Phân Tích Ảnh Hưởng Của Cọc Bên Trong Hố Đào Ứng Với Công Trình Thực Tế
Phân Tích Ảnh Hưởng Của Cọc Bên Trong Hố Đào Ứng Với Công Trình Thực Tế -
 Thông Số Thanh Chống Xiên Và Giằng Đầu Cừ Larsen
Thông Số Thanh Chống Xiên Và Giằng Đầu Cừ Larsen
Xem toàn bộ 90 trang tài liệu này.
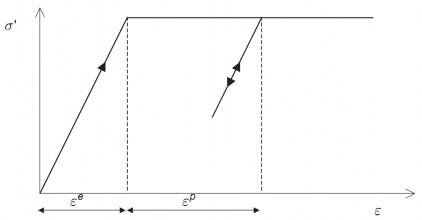
Hình 4.5 – Mô hình dẻo lý tưởng
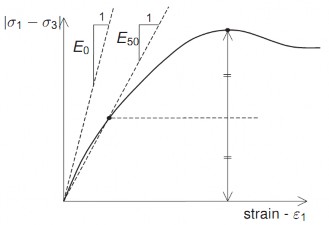
Hình 2.6 – Xác định Eo và E50 qua thí nghiệm nén 3 trục thoát nước
2.4.2. Mô hình Hardening Soil (HS)
Đáp ứng đất khi chịu tải trọng là không tuyến tính, không đàn hồi và rất là phụ thuộc vào cường độ của ứng suất. Mô hình đàn hồi không tuyến tính có thể được