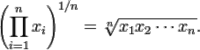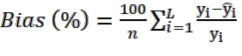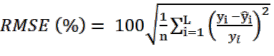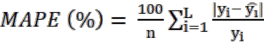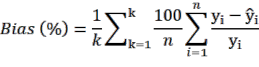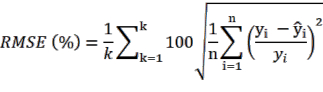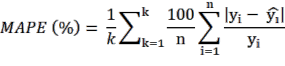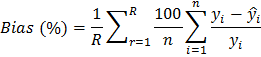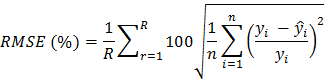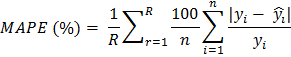Trong đó: RMSE: Root Mean Squared Error: Sai số trung phương; y’ là đạo hàm bậc nhất của biến phụ thuộc y và bằng 1; nếu biến phụ thuộc được đổi biến số là ln(y) thì sẽ bằng 1/y.
Công thức tính trung bình hình học (Geometric mean):
| (2.5) |
Có thể bạn quan tâm!
-
Thẩm Định Chéo (Cross-Validation) Mô Hình Sinh Trắc -
Ứng Dụng Hệ Thống Mô Hình Sinh Khối Cây Rừng Để Ước Tính Carbon Tích Lũy Trong Bể Chứa Trong Cây Rừng Trên Mặt Đất -
Thu Thập Số Liệu Sinh Khối Trên Cây Mẫu Chặt Hạ Và Dữ Liệu Sinh Thái Môi Trường Và Lâm Phần Nghiên Cứu -
Phương Pháp Thiết Lập Đồng Thời Hệ Thống Mô Hình Sinh Khối (Seemingly Unrelated Regression – Sur)) Và So Sánh Với Phương Pháp Thiết Lập Mô Hình Độc Lập -
Hệ Thống Mô Hình Sinh Khối Cây Rừng Theo Hệ Thống Phân Loại Thực Vật Áp Dụng Phương Pháp Thiết Lập Mô Hình Độc Lập -
Hệ Thống Mô Hình Ước Tính Đồng Thời Sinh Khối Theo Sur Và So Sánh Với Phương Pháp Thiết Lập Mô Hình Độc Lập
Xem toàn bộ 207 trang tài liệu này.
2.3.3.2 Phương pháp thẩm định chéo mô hình sinh khối cây rừng (Cross Validation) để xác định sai số và lựa chọn mô hình
Nghiên cứu này thử nghiệm ba phương pháp thẩm định chéo mô hình sinh khối
Phương pháp thẩm định chéo - Leave-One-Out Cross Validation (LOOCV):
Từ n dữ liệu cây mẫu, phương pháp Leave-One-Out Cross Validation (LOOCV) sử dụng n-1 dữ liệu lập mô hình và 1 dữ liệu độc lập dùng để đánh giá sai số. Mỗi lần như vậy tính toán các chỉ tiêu thống kê đánh giá, so sánh các mô hình như AIC (Akaike information criterion), hệ số xác định R2 và các sai số như Bias%, RMSE%, MAPE%. Lặp lại như vậy với n lần lập mô hình và đánh giá sai số, với sai số mỗi lần được tính từ một dữ liệu độc lập không tham gia lập mô hình, sau đó lấy trung bình (Moore, 2017).
Cách tính các sai số tương đối khi áp dụng LOOCV (Bảo Huy, 2017):
(2.6) | |
| (2.7) |
(2.8) |
Trong đó, L là số lần lặp lại tính sai số, mỗi lần sử dụng một dữ liệu độc
lập để tính sai số mô hình (L = n dữ liệu); 
và 
là giá trị quan sát và dự đoán qua mô hình.
Phương pháp thẩm định chéo - K-Fold
Phương pháp này phân chia dữ liệu thành K phần bằng nhau (K-Fold) (Kohavi, 1995; Picard và ctv, 2012), phổ biến với K = 10 thì một phần dữ liệu (1/10 dữ liệu) không tham gia lập mô hình dùng để đánh giá sai số, trong khi đó K-1 phần dữ liệu (9/10 dữ liệu) dùng lập mô hình. Mỗi lần như vậy tính toán các chỉ tiêu thống kê đánh giá, so sánh các mô hình như AIC, R2 và các sai số như Bias%, RMSE%, MAPE%. Tiến hành lặp lại như vậy K = 10 lần, và tính sai số trung bình từ K lần lặp (Moore, 2017).
Cách tính các sai số tương đối theo phương pháp k-fold như sau (Bảo Huy 2017):
(2.9) | |
| (2.10) |
| (2.11) |
Trong đó, k là số phần dữ liệu bằng nhau được phân chia (k-fold), với k
= 10; n là số dữ liệu đánh giá của mỗi lần và 
, 
là giá trị quan sát và dự đoán qua mô hình.
Phương pháp thẩm định chéo - Monte Carlo
Phương pháp Monte Carlo dùng để thẩm định chéo các mô hình sinh khối được mô tả như sau: Phân chia dữ liệu ngẫu nhiên làm 2 phần, một phần dùng để lập mô hình (80% dữ liệu) và một phần dùng để đánh giá sai số (20% dữ liệu). Mỗi lần như vậy tính toán các chỉ tiêu thống kê đánh giá, so sánh các mô hình như AIC, R2 và các sai số như Bias%, RMSE%, MAPE%. Tiến hành lặp lại như vậy R = 200 lần để thẩm định các mô hình và đánh giá sai số, cuối cùng giá trị thống kê so sánh các mô hình và sai số được tính trung bình từ 200 lần thẩm định chéo (Temesgen và ctv, 2014 và Huy và ctv, 2016a,b).
Các sai số áp dụng theo phương pháp thẩm định chéo Monte Carlo với R lần lặp lại ngẫu nhiên như sau (Swanson và ctv, 2011; Huy và ctv, 2016a,b,c):
(2.12) | |
| (2.13) |
| (2.14) |
Trong đó, R = 200 là số lần phân chia dữ liệu ngẫu nhiên thành hai phần, n là số dữ liệu đánh giá của mỗi lần rút mẫu (20% mẫu rút ngẫu nhiên) và 
và 
là giá trị quan sát và dự đoán qua mô hình.
Công thức tính toán AIC như sau:
(2.15) |
Trong đó L là Likelihood của mô hình, p là tổng số tham số của mô hình.
Để lựa chọn mô hình tối ưu qua thẩm định chéo sai số, chỉ tiêu AIC là ưu tiên, mô hình có AIC bé nhất là tốt nhất, kết hợp với R2 càng cao càng tốt. Trong trường hợp các mô hình có AIC xấp xĩ nhau thì mô hình có các sai số bé hơn là có độ tin cậy hơn và được lựa chọn.
Trong xử lý số liệu theo các phương pháp thẩm định chéo, các phương pháp tính toán thông thường trên các phần mềm thống kê phổ biến như Excel, Statgraphics, SPSS, … không thể thực hiện được vì sự phức tạp của phân chia dữ liệu ngẫu nhiên, chạy mô hình và tính các chỉ tiêu thống kê, sai số được lặp lại nhiều lần, do đó công việc này cần được lập Code để thực hiện trong phần mềm mã nguồn mở R hoặc SAS.
Cuối cùng, sau khi lựa chọn dạng mô hình nhờ thẩm định chéo và xác định được các sai số của mô hình lựa chọn, mô hình lựa chọn được thiết lập lại dựa vào toàn bộ dữ liệu.
2.3.4 Phương pháp thiết lập hệ thống mô hình sinh khối cây rừng theo hệ thống phân loại thực vật áp dụng phương pháp thiết lập mô hình độc lập
2.3.4.1 Lựa chọn biến số đầu vào, độc lập (Predictor(s)) cho mô hình sinh khối cây rừng khộp
Nghiên cứu này sử dụng biến đầu vào quan trọng cho mô hình sinh khối là đường kính ngang ngực (ở độ cao 1,3 m so với mặt đất (D, cm) trong tất cả hệ thống mô hình sinh khối, vì D luôn có quan hệ với sinh khối toàn bộ và thành phần, đồng thời đây là biến cơ bản và dễ đo đạc trong điều tra rừng (Brown và ctv, 1989, 1997, 2001; Brown và Iverson, 1992).
Ngoài ra nghiên cứu này được tiến hành trên các vùng sinh thái khác nhau của rừng khộp, vì vậy biến đầu vào chiều cao cây rừng (H, m) cũng
được nghiên cứu, đánh giá để phản ánh sự khác nhau của lập địa ảnh hưởng đến tích lũy sinh khối cây rừng (Basuki và ctv, 2009; Chave và ctv, 2005, 2014; Huy và ctv, 2016a,b,c; Kralicek và ctv, 2017).
Đồng thời rừng khộp là kiểu rừng hỗn loài khác tuổi, vì vậy biến đầu vào khối lượng thể tích gỗ (WD (g/cm3) cũng được sử dụng để phản ánh khả năng tích lũy sinh khối/carbon khác nhau theo loài (Basuki và ctv, 2009; Chave và ctv, 2005, 2014; Huy và ctv, 2016a,b,c; Kralicek và ctv, 2017)
Như vậy nghiên cứu này thử nghiệm ba biến số đầu vào cho mô hình ước tính AGB và sinh khối các bộ phận (bao gồm sinh khối thân Bst (kg), sinh khối cành Bbr (kg), sinh khối lá Ble (kg) và sinh khối vỏ cây Bba (kg): Đó là D (cm), H (m) và WD (g/cm3), đồng thời sử dụng tổ hợp các biến, bao gồm:
D2H (m3) = 
) là đại diện cho thể tích cây gỗ, và tổ hợp D2HWD (kg)
= D2H×WD×1000) là đại diện cho sinh khối thân cây gỗ.
2.3.4.2 Chọn dạng phương trình sinh khối cây rừng
Dựa trên đã công bố trong và ngoài nước (Brown, 1997; Basuki và ctv, 2009; Chave và ctv, 2005, 2014; Picard và ctv, 2015; Huy và ctv, 2016 a,b,c), luận án sử dụng dạng hàm Power như là dạng phương trình sinh khối trong nghiên cứu này.
Ngoài ra Hình 2.3 và Hình 2.4 cũng cho thấy AGB và các thành phần sinh khối của cây rừng khộp theo hệ thống phân loại thực vật cũng quan hệ với D theo hàm Power, trong đó sinh khối có xu hướng tăng mạnh khi D tăng. Do đó, nghiên cứu này áp dụng hàm Power để lập và thẩm định hệ thống mô hình sinh khối cây rừng khộp với các biến số đầu vào khác nhau.
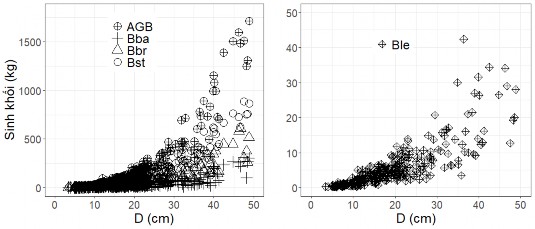
Hình 2.3. Phân bố sinh khối thân cây (Bst, kg), cành (Bbr, kg), lá (Ble, kg), vỏ cây (Bba, kg) và tổng sinh khối cây rừng khộp trên mặt đất (AGB, kg) theo đường kính ngang ngực (D, cm) trong trường hợp chung loài.
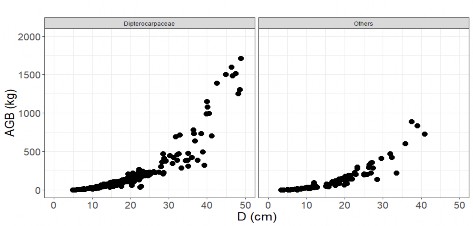
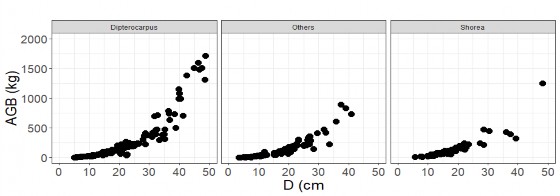
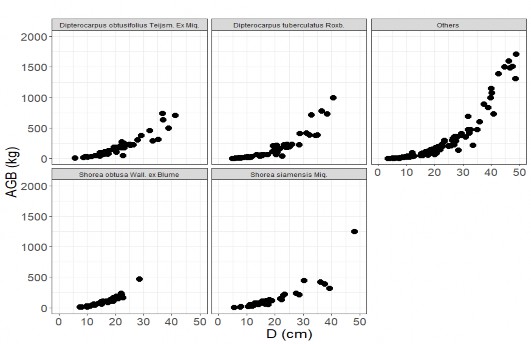
Hình 2.4. Quan hệ AGB theo D theo hệ thống phân loại thực vật ưu thế rừng khộp
2.3.4.3 Ước lượng mô hình sinh khối có trọng số
Các mô hình phi tuyến tính dạng Power được áp dụng trọng số để điều chỉnh độ không đồng nhất trong sai số ở các cây có kích thước khác nhau do hiện tượng phân hóa biến sinh khối mạnh khi kích thước cây tăng lên (heteroscedasticity) (Hình 2.5) (Davidian và Giltinan, 1995; Picard và ctv, 2012; Huy và ctv, 2016a,b,c; Kralicek và ctv, 2017).
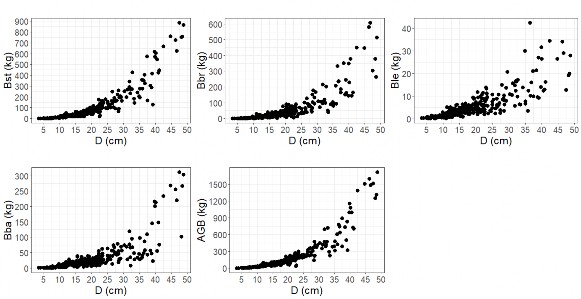
Hình 2.5. Phân hóa mạnh dữ liệu sinh khối khi kích thước cây tăng lên theo hiện tượng heteroscedasticity
2.3.4.4 Phương pháp lập mô hình phi tuyến tính có trọng số theo phương pháp “Hợp lý cực đại” (Weighted Non-Linear Fixed by Maximum Likelihood)
Sử dụng phương pháp Maximum Likelihood có trọng số để thiết lập mô hình phi tuyến (Weighted Nonlinear Fixed Models fit by Maximum Likelihood) với kiểu dạng mô hình power tổng quát như sau (Huy và ctv, 2016a,b,c; Kralicek và ctv, 2017):
(2.16) | |
| (2.17) |
Trong đó 
là Bst, Bba, Bbr, Bl, AGB (kg) ứng với cây thứ j; 
và 
là tham số của mô hình; 
là các biến số D (cm), H (m), WD (g/cm3), hoặc tổ
hợp biến đại diện cho thể tích cây: D2H hoặc tổ hợp biến đại diện cho sinh khối: D2HWD ứng với cây thứ j và là sai số ngẫu nhiên ứng với cây thứ j.