Điều Kiện Cân Bằng Tĩnh Điện. Tính Chất Của Vật Dẫn Mang Điện

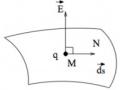
Một điện tích điểm

q 2 .109 C

nằm cách sợi dây dài tích điện đều một

khoảng r1=4cm; dưới tác dụng của điện trường do sợi dây gây ra, điện tích dịch chuyển theo hướng đường sức điện trường đến khoảng cách r2=2cm, khi

đó lực điện trường thực hiện công

Bài 1.18.

A  50.107 J . Tính mật độ điện dài của dây.

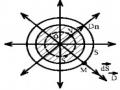
Một vòng dây bán kính 4cm tích điện đều với điện tích Q 1 .109 C. Tính

Có thể bạn quan tâm!

Xem toàn bộ 258 trang tài liệu này.

điện thế tại:

a. Tâm vòng dây

b. Một điểm M trên trục vòng dây, cách tâm của vòng dây h=3cm.

Bài 1.19.

Cho hai mặt phẳng song song vô hạn mạng điện tích đều, mật độ bằng nhau và trái dấu nhau, đặt cách nhau 5mm. Cường độ điện trường giữa chúng là 104V / m . Tính hiệu điện thế giữa hai mặt phẳng đó.

Bài 1.20.

Tại hai đỉnh C, D của một hình chữ nhật ABCD (có các cạnh

AB  4cm, BC  3cm ), người ta đặt hai điện tích điểm q 3.108C tại C,

8

q2  3.10 C tại D. Tính hiệu điện thế giữa A và B.

Bài 1.21.

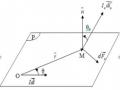
Có một điện tích điểm q đặt tại tâm O của hai đường tròn đồng tâm bán kính r và R. Qua tâm O ta vẽ một đường thẳng cắt hai đường tròn tại các điểm A, B, C, D (Hình 3).

A B

C D

Hình 3

a. Tính công của lực điện trường khi dịch chuyển một điện tích q0 từ A

đến C và từ A đến D.

b. So sánh công của lực tĩnh điện khi dịch chuyển điện tích q0 từ A đến C

và từ C đến D.

Chương 2.VẬT DẪN

2.1. ĐIỀU KIỆN CÂN BẰNG TĨNH ĐIỆN. TÍNH CHẤT CỦA VẬT DẪN MANG ĐIỆN

2.1.1. Định nghĩa vật dẫn cân bằng tĩnh điện

Một vật dân

đươc

tích đi ện mà các haṭ mang đi ện của nó ch ỉ tham gia

chuyển động nhiệt hỗn loạn chứ không tham gia chuyển động có định hướng

(tạo thành dòng điện), đươc

goi

là vật dân

cân bằng tin

h điện.

2.1.2. Điều kiện cân bằng tĩnh điện

Vectơ cường độ điện trườ ng E tại mọi điểm trong vật dân điện bằng không:

cân bằng tinh

Etr  0

Thật vậy, nếu Etr  0thì F  0 kéo các điện tích chuyển động có hướng tạo thành dòng điện bên trong vật dẫn nghĩa là không thỏa mãn điều kiện cân bằng tĩnh điện.

Tại mọi điểm trên bề m ặt của v ật dân

cân bằng tin

h đi ện, vectơ E (do

đó cả đườ ng sứ c điện trườ ng nữa) phải vuông góc với bề mặt vật dân:

Emat En, Et  0

Thật vậy, nếu taị một điểm nào đó trên bề mặt vật dân

cân bằng tin

h điện

có véctơE không vuông góc với bề m ặt, khi đó ta phân tích E Et En và chắc chắn thành phần tiếp tuyến với bề mặt Et 0 . Do vậy một điện tích bất kỳ nằm ở đó sẽ chịu tác dụng của lực tiếp tuyến với bề m ặt Ft qEt 0 khiến

q bị dịch chuyển, vật dân

không còn ở traṇ g thái cân bằng tĩnh điện nữa.

2.1.3. Những tính chất của vật dẫn mang điện.

Vật dân

cân bằng tin

h đi ện là một khối đẳng thế , bề mặt vật dân

là m ột

mặt đẳng thế.

Thật vậy, xét hai điểm M, N bất kỳ nằm trên vật dân và L là đường cong

AN

bất kỳ nối hai điểm đó, ta có: VM VN MNEdS ,

q M

 Nếu M,N nằm bên trong vật dẫn:

E Etr  0 VM VN

tứ c là V = const bên trong lòng vật dân.

 Nếu M,N nằm trên mặt vật dẫn:

 

N



E En VM VN En dS  0 vì En dS VM VN

nên mặt vật dân là một mặt đẳng thê.́

 Do tính chất liên tục của điện thế nên điện thế tại một điểm sát mặt vật dẫn bằng điện thế trên mặt vật dẫn.

Vậy toàn bộ vật là một khối đẳng thế.

Điện tích chỉ phân bố trên bề mặt của vật dân

cân bằng tin

h điện.

Thật vậy, nếu chon

S là một mặt kín nằm tron

trong lòng v ật dân

và rất

sát với bề mặt vật dân

, khi đó áp dun

g điṇ h lý O-G cho mặt kín S này ta có:

qiDtr .dS  0

i  (S )

vì Dtr  0 qi 0

Vì mặt kín S được chọn bất kì nên các điện tích không phân bố trong lòng vật dẫn, chỉ phân trên bề mặt vật dẫn.

 Đối với một vật dẫn rỗng đã ở trạng thái cân bằng tĩnh điện, điện trường ở phần rỗng và thành trong của vật dẫn rỗng cũng luôn luôn bằng 0.

 Nếu đem một quả cầu kim loại mang điện cho tiếp xúc với mặt trong của vật dẫn rỗng thì điện tích trên quả cầu mang điện sẽ được truyền hết ra mặt ngoài vật dẫn rỗng.

Sự phân bố điện tích trên mặt vật dẫn chỉ phụ thuộc vào hình dạng của mặt đó. Điện tích được tập trung ở những chỗ có mũi nhọn. Vì lí do đối xứng, trên những vật dẫn có dạng mặt cầu, mặt phẳng vô hạn, mặt trụ dài vô hạn, điện tích được phân bố đều.

Bài toán 1:

Một quả cầu kim loại đặt trong chân không có bán kính bằng 50cm ,

mang một điện tích một điểm:

q  5.105 C . Xác định cường độ điện trường và điện thế tại

a. Nằm cách mặt quả cầu 100cm ;

b. Nằm sát mặt quả cầu;

c. Ở tâm quả cầu.

Giải:

q  5.105 C



a. EM , VM ?



Cho R  50cm  5.101 m

Hỏi

b. EN

,VN ?

l  10cm  1m c. E ,V ?

0 0

a. Cường độ điện trường và điện thế do một quả cầu kim loại mang điện tích gây ra tại một điểm nằm ngoài quả cầu bằng cường độ điện trường và điện thế gây bởi một điện tích điểm có điện tích bằng điện tích của quả cầu đặt tại tâm của nó.

Gọi r là khoảng cách từ tâm O của quả cầu đến điểm M mà ta xét, thì:

EM 

40r

 2.105V / m,

VM 

40r

 3.105V .

b. Cường độ điện trường ngay trên mặt quả cầu thì không xác định được, nhưng tại một điểm nằm sát mặt quả cầu vẫn được xác định gần đúng theo công thức trên:

1 5.105 6

EN  4

(50)2 .104  1,8.10 V / m,

1 5.105 5

VN  4

5.102  9.10 V .

c. Cường độ điện trường tại tâm quả cầu bằng không vì quả cầu kim loại

cân bằng tĩnh điện (E0  0) .

Điện thế tại tâm quả cầu bằng điện thế tại một điểm trên mặt quả cầu vì quả cầu kim loại là một vật đẳng thế.

Do đó: V0

 9.105V.

2.2. HIỆN TƯỢNG ĐIỆN HƯỞNG

2.2.1. Hiện tượng điện hưởng. Định lý các phần tử tương ứng

a. Hiện tượng điện hưởng

Khi đặt một vật dẫn B chưa mang điện trong một điện trường ngoài E 0 . Dưới tác dụng của lực điện trường các

electron trong vật dẫn B sẽ chuyển động

trong vật dẫn ngược chiều điện trường. Kết quả trên hai mặt giới hạn của vật dẫn B xuất hiện các điện tích trái dấu. Các điện tích này gọi là các điện tích cảm ứng.

Hình 2.1. Hiện tượng điện hưởng

Các điện tích cảm ứng gây ra bên trong vật dẫn B một điện trường phụ

E ngày càng lớn. Đến một lúc nào đó E đủ lớn, cân bằng E làm cho điện

trường tổng hợp trong vật dẫn E E E  0. Khi đó, các điện tích ngừng chuyển động. Vì vậy, vật dẫn ở trạng thái cân bằng tĩnh điện.

Hiện tượng các điện tích cảm ứng xuất hiện trên vật dẫn (lúc đầu không mang điện) khi đặt trong điện trường ngoài gọi là hiện tượng điện hưởng.

b. Định lí các phần tử tương ứng

Xét tập hợp đường cảm ứng tựa trên chu vi của phân tử diện tích S trên

vật A. Giả sử tập hợp này tới diện tích

S

trên B. Các thành phần diện tích

S và

S

được chọn như trên được gọi là các thành phần tử tương ứng.

Xét mặt kín (S) hợp bởi ống đường cảm ứng nêu trên và hai mặt tựa trên

diện tích S và S.

Từ thông gửi qua mặt kín:

Định lý:

CD.dS qiq q 0

(S )

q q

Điện tích cảm ứng trên các phần tử tương ứng có độ lớn bằng nhau và trái dấu nhau.

2.2.2. Điện hưởng một phần và điện hưởng toàn phần

a. Điện hưởng một phần

Là hiện tượng vật lý mà chỉ có một số đường cảm ứng điện xuất phát từ vật mang điện (A) tới được vật dẫn (B), còn một số đường cảm ứng điện từ A lại đi xa vô cùng:

qq

Trong trường hợp điện hưởng một phần, độ lớn của điện tích cảm ứng nhỏ hơn độ lớn điện tích trên vật mang điện.

b. Điện hưởng toàn phần

Là hiện tượng toàn bộ các đường cảm ứng điện xuất phát từ (A) đều đi tới (B):

qq

Trong trường hợp điện hưởng toàn phần, độ lớn của điện tích cảm ứng bằng độ lớn điện tích trên vật mang điện.

2.3. ĐIỆN DUNG CỦA MỘT VẬT DẪN CÔ LẬP

2.3.1. Định nghĩa

Một vật dân

đươc

goi

là cô l ập về điện nếu gần nó không có m ột vật nào

khác có thể gây ảnh hưởng đến sự phân bố điện tích trên vật dân đang xét.

Khi ta truyền cho v ật dân

A một điện tích Q nào đó. Theo tính chất của

vật dân

mang điện (đã ở traṇ g thái cân bằng tin

h điện), điện tích Q đươc

phân

bố trên bề mặt vật dân

sao cho điện trường trong lòng vật dân

bằng không.

Thưc nghiệm cho thấy: nêú ta thay đổi giá tri ̣đi ện tích Q của vật dân cô

lập và đo điện thế V của nó thì tỉ số giữa Q và V luôn luôn không thay đổi. Nghĩa là điện thế V của vật dẫn cô lập tỉ lệ với điện tích Q của vật dẫn đó:

Q CV

C là hằng số đặc trưng cho khả nă ng tích đi ện của vật ở điện thế V nhất điṇ h

nào đó, đươc

goi

là điện dung của vật dẫn, C phụ thuộc hình dạng kích thước

và tính chất của môi trường cách điện bao quanh.

Vậy:Điện dung của một vật dẫn cô lập là một đại lượng về giá trị bằng điện tích mà vật dẫn tích điện được khi điện thế của nó bằng một đơn vị điện thế.

Đơn vị

Đơn vị của C là Fara (F): 1Fara 1Culong ,

1Von

1F  106 F , 1nF  109 F, 1pF  1012 F.

2.3.2. Điện dung của một quả cầu kim loại

C Q Q  4R

V Q0

40 R

2.4. HỆ VẬT DẪN TÍCH ĐIỆN CÂN BẰNG. TỤ ĐIỆN

2.4.1. Điện dung và hệ số điện hưởng

Xét hệ 3 vật dẫn tích điện ở trạng thái cân bằng có các giá trị điện tích và

điện thế lần lượt là:

q1, q2 , q3

và V1,V2 ,V3.

Đối với vật dẫn cô lập:

q CV

Đối với hệ 3 điện tích trên:

Trong đó:

q1 C11V1 C12V2 C13V3 q2 C21V1 C22V2 C23V3 q3 C31V1 C32V2 C33V3

Cii  0 và Cik Cki

(i, k  1, 2,3).

C11, C22, C33 là điện dung của các vật dẫn 1, 2 và 3.

C12, C13, …..C32 là các hệ số điện hưởng.

2.4.2. Tụ điện

a. Định nghĩa

Tụ điện là một hệ hai vật dẫn A và B sao cho vật dẫn B bao bọc hoàn toàn vật dẫn A. Do đó A và B ở trạng thái điện hưởng toàn phần.

Giả sử A tích điện q1 (mặt ngoài), mặt trong của B tích điện q2, mặt ngoài



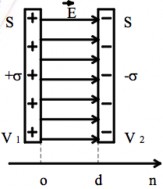
B xuất hiện điện tích q2

b. Tính chất

Tính chất 1:

q1 q2  0

Chứng minh: Do A, B ở trạng thái hưởng điện hoàn phần.

Tính chất 2:

Hình 2.2. Tụ điện phẳng

 Liên hệ giữa điện tích 2 vật A, B và điện thế giữa chúng.

 Vật A: q1 C11V1 C12V2

 Vật B: q2 q'2 C21V1 C22V2

 Nếu B được nối đất thì q truyền xuống đất:

q'2  0, V2 Vd  0.