Tập đỉnh đích DICH
Output:
Đường đi từ đỉnh n0 đến DICH Procedure HCS; {Hill Climbing Search} begin
Push(MO,n0);
while MO <> null do begin
i = Pop(MO);
if T(i) DICH <> null then begin
end;
L:= null;
for j T(i) do
if j chưa xét then
đưa j vào danh sách L sắp xếp L theo thứ tự hàm đánh giá;
chuyển danh sách L vào đầu danh sách MO;
write (‘Khong co loi giai’);
end;
4.6.3. Nhận xét.
Phương pháp tìm kiếm leo đồi chú trọng tìm hướng đi dễ dẫn đến trạng thái đích nhất. Cách đó được đưa ra nhằm làm giảm công sức tìm kiếm. Thuật toán tìm kiếm leo đồi thực chất là thuật toán tìm kiếm theo chiều sâu, song tại mỗi bước ta sẽ ưu tiên chọn một trạng thái có hứa hẹn nhanh tới đich nhất để phát triển trước. Thông thường ta gán mỗi trạng thái của bài toán với một số đo (hàm đánh giá) nào đó nhằm đánh giá mức độ gần đích của nó. Điều đó có nghĩa là nếu trạng thái hiện thời là u thì trạng thái v sẽ được phát triển tiếp theo nếu v kề với u và hàm đanh giá của v đạt giá trị max (hoặc min).
Tuy nhiên phương pháp này không được cải thiện so với các phương pháp khác trong một số trường hợp sau:
Cực trị địa phương: nút đang xét tốt hơn các nút lân cận, nhưng đó không phải là phương án tốt nhất trong toàn thể, ví vậy có thể phải quay lui về nút trước để đi theo hướng khác.
Cao nguyên bằng phẳng: Các giá trị của các phương án như nhau, không xác định được ngay hướng nào là tốt hơn trong vùng lân cận.
4.6.4. Các ví dụ.
Ví dụ 1. Bài toán trò chơi 8 số.
2 | 8 | 3 |
1 | 6 | 4 |
7 | 5 |
Có thể bạn quan tâm!
-
Đánh Giá Độ Phức Tạp Của Giải Thuật Tìm Kiếm Rộng. -
Phương Pháp Tìm Kiếm Tốt Nhất Đầu Tiên (Best First Search). -
Trí tuệ nhân tạo - TS. Nguyễn Ngọc Thuần - 12
Xem toàn bộ 105 trang tài liệu này.
1 | 2 | 3 |
8 | 4 | |
7 | 6 | 5 |
trạng thái đầu trạng thái đích
Trong bài toán này, ta sử dụng hàm đánh giá h như sau:
h(u) là số các chữ số trong trạng thái u không trùng với vị trí của nó trong trạng thái đích. Trạng thái có tiềm năng dẫn đến đích nhanh nhất (được ưu tiên phát triển trước) là trạng thái có hàm đánh giá h đạt giá trị min..
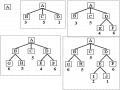
Trạng thái được chọn đi tiếp ở hướng mũi tên. Ở mức 3 chúng ta thấy có hai trạng thái cùng giá trị hàm đánh giá (= 3). Đây là trương hợp “cao nguyên băng phẳng” như nhận xét trên, nếu ta chọn phương án kia thì chắc chắn quá trình tìm kiếm sẽ khác đi nhiều. ( Bài tập dành cho Sinh viên).
Minh hoạ cây tìm kiếm cho bài toán này theo giải thuật leo đồi như sau :
8 | 3 | |
1 | 6 | 4 |
7 | 5 |
2
8
3
1
4
7
6
5
h(u) = 4
2 | 8 | 3 |
1 | 6 | 4 |
7 | 5 |
2 | 8 | 3 |
1 | 6 | 4 |
7 | 5 |
h(u) = 5 h(u) = 3 h(u) = 5
8 | 3 | |
1 | 4 | |
7 | 6 | 5 |
2 | 3 | |
1 | 8 | 4 |
7 | 6 | 5 |
2 | 8 | 3 |
1 | 4 | |
7 | 6 | 5 |
h(u) = 3 h(u) = 3 h(u) = 4
2 | 3 | |
1 | 8 | 4 |
7 | 6 | 5 |
2 | 3 | |
1 | 8 | 4 |
7 | 6 | 5 |
h(u) = 2 h(u) = 4
2 | 3 | |
8 | 4 | |
7 | 6 | 5 |
h(u) = 1
2 | 3 | |
8 | 4 | |
7 | 6 | 5 |
TÀI LIỆU THAM KHẢO
1. Nguyễn Thanh Thuỷ, Trí tuệ nhân tạo - Các phương pháp giải quyết vấn đề và kỹ thuật xử lý tri thức, NXB GD, 1999
2. Bạch Hưng Khang, Hoàng Kiếm, Trí tuệ nhân tạo - Các phương pháp và ứng dụng, Nhà xuất bản Khoa học kỹ thuật, 1989
3. Đỗ Trung Tuấn, Trí tuệ nhân tạo, Nhà xuất bản giáo dục, 1998.
[4]. Bùi Xuân Toại, Trương Gia Việt (Biên dịch), Trí tuệnhân tạo - Các cấu trúc và chiến lược giải quyết vấn đề, NXB Thống kê, 2000
[5]. Deepak Khemani, First Course in Artificial Intelligence, MC Graw-Hill Education, New Delhi, 2014.