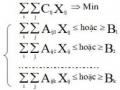Các Biến Điểm Trung Chuyển Và Thời Gian Di Chuyển Qua Các Điểm [6] ‌

Mô hình LP có thể được thiết lập, tìm ra các điểm tối ưu và số lượng ôtô cần thiết cho hoạt động của mỏ [55]. Trong mô hình LP này, mỗi điểm chất tải và dỡ tải được gọi là các “nút” (hình 2.5).

Mỗi “điểm” là chỗ kết nối trực tiếp từng nút, đại diện cho một tuyến đường vận tải. Biến Xij được định nghĩa là điểm “mật độ dòng” (số ôtô vận tải trên một chặng đường trong một phút) xuyên suốt các điểm từ nút i đến nút j. Mỗi điểm từ nút i đến nút j tương ứng với thời gian di chuyển Tij trên toàn tuyến đường. Xij là biến trực tiếp, vì vậy nó không tương đương với Xji, (hình 2.5).

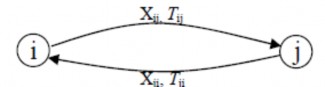
Hình 2.5. Các biến điểm trung chuyển và thời gian di chuyển qua các điểm [6]‌

Số lượng ôtô cần thiết trên toàn tuyến đường từ nút i đến nút j được tính bằng cách nhân số tuyến mật độ dòng Xij (số ôtô trên phút) trên toàn tuyến với thời gian Tij (phút) cần thiết để di chuyển trên toàn tuyến đường. Hình 2.6 minh họa biến Xij và thời gian tương ứng Tij trong quy trình hoạt động của một ôtô đơn giản.

Minh họa mô hình LP đơn giản xác định Xij và Tij tương ứng với 2 khu vực chất tải [6]‌

Mục tiêu của mô hình LP đơn giản là giảm thiểu số lượng ôtô cần thiết cho dây chuyền sản xuất trên mỏ. Số ôtô cần thiết phục vụ cho mỏ là tổng số ôtô cần thiết tại mỗi điểm, từ điểm chất tải đến điểm dỡ tải, có thể được tính như sau [6]:

Có thể bạn quan tâm!

• Năng Suất Thiết Bị Vận Tải Của Mỏ Than Cọc Sáu Năm 2016 [11]
• Tổng Quan Về Một Số Thuật Toán Trong Nước Dùng Để Tính Toán Đồng Bộ Máy Xúc - Ôtô
• Sơ Đồ Chuyển Đổi Từ Trạng Thái Này Snag Trạng Thái Khác Của Tổ Hợp Ôtô - Máy Xúc [20] ‌
• Nguyên Tắc Hoạt Động Của Phương Pháp Monte Carlo [1]
• Nhóm Các Phương Pháp Sử Dụng Trí Tuệ Nhân Tạo:
• Đối Với Nhóm Các Phương Pháp, Thuật Toán Trong Nước Sử Dụng Để Tính Toán Sự Phối Hợp Giữa Máy Xúc – Ôtô:

Xem toàn bộ 217 trang tài liệu này.

Min Z 

Tij *X ij 

(i, j)PS

Tji *X ji 

( j,i)PD

Si* X ij 

(i, j)PS

Dj *X ji

( j,i)PD

(2.26)

Trong đó: i, j - các chỉ số cho nút đầu và cuối; Xij - mật độ dòng (ôtô trên phút) của tất cả các điểm từ nút nguồn i đến nút j; Xji - mật độ dòng (xe ôtô trên phút) của các điểm từ nút j đến nút i; Tij - thời gian di chuyển trung bình (phút) qua các điểm từ nút i đến nút j; Tji - thời gian di chuyển trung bình (phút) qua các điểm từ nút j đến nút i; Si - thời gian chất tải trung bình (phút) tại nút i; Dj - thời gian dỡ tải trung bình (phút) tại nút j; PS - tổng các điểm (i, j) từ các nút nguồn i đến nút đích j; PD - tổng các điểm (j, i) từ tất cả các điểm nút j tới điểm nguồn nút i.

Để tận dụng năng lực tối ưu của các điểm chất tải, các ôtô được bố trí đến các điểm chất tải để không có điểm nào phải trong tình trạng máy xúc chờ ôtô. Mỗi điểm nhận tải sẽ chất tải lên ôtô theo mật độ dòng hạn chế:

Tốc độ dòng khống chế cho mỗi điểm chất tải xác định như sau [6]:

X ij Ri

j

 0 với i SS

(2.27)

Trong đó: Ri - nút mà mật độ dòng ở ngưỡng tốc độ dòng giới hạn tại nút i (ôtô trên phút); SS - tập hợp tất cả các nút.

Trong quá trình chất tải lên ôtô, các ôtô sẽ di chuyển tới các điểm dỡ tải và đổ tải. Sau khi dỡ tải các ôtô quay về điểm nhận tải. Vấn đề đặt ra là tại mỗi nút cần kiểm soát được quá trình chất tải và dỡ tải, tức là phải cân bằng được tốc độ ra vào khi nhận tải tại mỗi điểm nút.

Giả thiết rằng mật độ dòng tại nút vào sẽ ký hiệu dấu âm (-) và mật độ dòng lúc ra khỏi nút sẽ mang giá trị dương (+). Như vậy, giá trị cân bằng cho mỗi nút j có thể được biểu diễn thông qua công thức sau [6]:

X ij X jk i k

(2.28)

 0 với j  (SS, SD)

Mật độ dòng đối với mỗi biến là giá trị không âm, tức là

Xij  0 với (i, j)

Như vậy, mô hình LP đơn giản đã giải quyết được bài toán xác định số lượng ôtô cần thiết phục vụ cho mỏ sao cho các thiết bị xúc bốc không phải chờ đợi ôtô trong trường hợp tổng quát với giả thiết cùng một chủng loại ôtô và máy xúc, cùng cung độ vận tải và sơ đồ công nghệ như hình 2.6.

b. Mô hình LP mở rộng với việc phân phối ôtô trên mỏ lộ thiên [6]

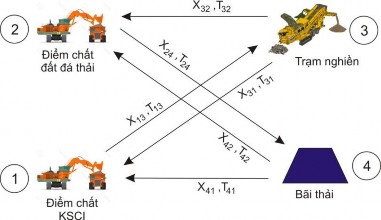
Hình 2.7 minh họa một chu trình mỏ bao gồm 3 điểm xếp hàng (được coi như là nút nguồn) và có 3 điểm đích đến, bao gồm trạm nghiền, kho chứa và bãi thải.

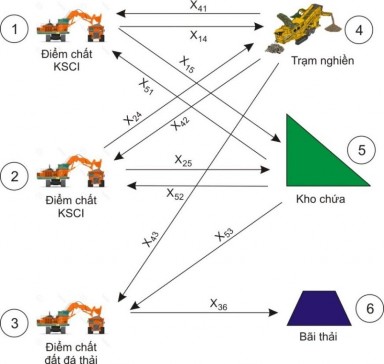
Hình 2.7. Minh họa mô hình LP mở rộng với 3 khu vực chất tải

Tất cả các nút đều kết nối với nhau qua các đường đi. Biến Xij được coi là đoạn “tốc độ dòng” (tấn trên giờ) qua mỗi chặng đường từ nút i đến nút j. Mỗi đoạn đường từ nút i đến nút j tương ứng với thời gian vận chuyển Tij (tính bằng giờ) trên toàn tuyến đường đó. Mục tiêu của mô hình LP này là hạn chế tối đa tổng số lượng xe ôtô cần dùng cho hoạt động mỏ, trong khi vẫn đáp ứng yêu cầu trung hòa quặng và hạn chế sự tiêu tốn nguyên vật liệu khi đến điểm đích trong khi vẫn đảm bảo tỷ lệ/tốc độ sản xuất tại điểm nguồn xuất phát [56].

Mục tiêu của mô hình LP mở rộng này là hạn chế tổng số ôtô cần sử dụng cho mỏ và được thể hiện bằng công thức sau [6]:

Z Tij * Xij 

(i, j)PS

Tji *X ji 

( j,i)PD

Si* Xij 

(i, j)PS

Dj *X ji

( j,i)PD

(2.29)

Trong đó: i, j - các biến đại diện cho nút đầu và cuối; Xij - tốc độ dòng (t/h) của chặng đường từ nút i đến nút j; Xji - tốc độ dòng (t/h) của chặng đường từ nút j đến nút i; Tij - thời gian di chuyển trung bình (giờ) của ôtô trên chặng đường từ nút i đến nút j; Si - tổng thời gian chất tải (giờ) tại nút i; Dj - thời gian dỡ tải trung bình (giờ) tại nút j; PS - chuỗi các chặng đường (i, j) từ tất cả các nút đến điểm nút đích j; PD - chuỗi các chặng đường (j,i) từ tất cả các nút đích j đến nút nguồn i.

Tại mỗi nút, tổng tốc độ dòng (t/h) đi vào và đi ra từ các nút được tính cân bằng. Điều này có thể đạt được bằng cách dùng biến khống chế cân bằng, được thể hiện theo công thức sau [6]:

X ij X jk i k

(2.30)

 0 với j  (SS, SD)

Giả thiết mỗi nút nguồn i có năng suất làm việc là Ri (t/h). Tổng tốc độ dòng đi vào điểm chất tải tại nút i không thể lớn hơn năng suất làm việc tại điểm chất tải Ri. Giá trị khống chế năng suất làm việc cho mỗi nút nguồn i có thể xác định như sau:

X ij Ri  0 với j SS

j

(2.31)

Trong đó: Ri - năng suất làm việc tại nút nguồn i, t/h; SS - tập hợp tất cả các nút nguồn.

Tương tự như nút nguồn, mỗi nút điểm đích có thể có giá trị khống chế trọng tải. Giá trị này hạn chế tổng tốc độ dòng (t/h) có thể đi đến nút đích. Giá trị khống chế này đặc trưng cho một loại giới hạn tại điểm dỡ tải. Giới hạn trọng tải cho mỗi điểm đích nút j có thể trình bày như sau [6]:

X ij D j  0 với j SD

i

(2.32)

Trong đó: Dj - khối lượng dỡ tải tối đa tại điểm đích nút j, t/h; SD - tập hợp tất cả các nút đích.

Một giới hạn cần tính đến tại trạm nghiền hoặc kho chứa là mục tiêu trung hòa KSCI. Giới hạn trung hòa có thể có những yêu cầu cụ thể đối với khâu nghiền và dự trữ. Giới hạn này đảm bảo rằng trong thời gian nhất định cho phép trong khoảng thời gian hoạt động Tc chất lượng trung bình của KSCI sẽ nằm trong khoảng giới hạn yêu cầu về chất lượng khi đưa vào trung hòa. Giới hạn trung hòa tại mỗi nút đích có thể tính như sau [6]:

L j Aj

(Gi

i

Aj

Tc

M

) X ij

j

U j

(2.33)

Trong đó: Aj - giá trị trung bình hiện tại của giá trị KSCI pha trộn tại nút j; Gi - điểm trung bình của KSCI từ chặng đường Xij; Mj - khối lượng trung hòa tại nút j; Lj- giới hạn dưới của điểm quặng tại nút j; Uj - giới hạn trên của điểm quặng tại nút j; Tc- thời gian quy định trong khi hoạt động.

Số lượng ôtô có thể sử dụng được khống chế bằng cách dùng hệ số tổng trọng

tải xe Tact (tấn) và được xác định như sau [6]:

Z Tij * Xij 

(i, j)PS

Tji *X ji 

( j,i)PD

Si* Xij 

(i, j)PS

Dj *X ji Tact

( j,i)PD

(2.34)

Yêu cầu giá trị không âm:

X ij

 0 j ' s,i ' s

Như vậy, mô hình LP mở rộng này đã mở rộng tính toán cho việc trung hòa KSCI cũng như cho việc chất tải vào các kho chứa hoặc đưa ra các trạm nghiền. Mô hình này cũng đã giải quyết được bài toán xác định số ôtô cần thiết phục vụ cho mỏ sao cho các máy xúc không phải chờ đợi ôtô, quá trình sản xuất được hoạt động một cách nhịp nhàng.

2.2.2. Thuật toán Monte Carlo và ứng dụng của nó trên các mỏ lộ thiên

2.2.2.1. Tổng quan về phương pháp Monte Carlo

a. Lịch sử phát triển phương pháp Monte Carlo

Giữa thế kỷ XX, sự phát triển của các lĩnh vực quan trọng như vật lý hạt nhân, nguyên tử, các nghiên cứu vũ trụ, năng lượng, chế tạo các thiết bị phức tạp đòi hỏi phải tiến hành các bài toán lớn phức tạp, không thể giải được bằng các kỹ thuật có vào thời bấy giờ. Cùng với sự phát triển của máy tính điện tử đã làm xuất hiện khả năng mô tả định lượng đầy đủ các hiện tượng nghiên cứu và phạm vi giải các bài toán đã được mở rộng hơn. Những yếu tố trên đã góp phần hình thành nên việc thực nghiệm máy tính.

Thực nghiệm máy tính thực chất là áp dụng máy tính để giải các bài toán, nghiên cứu các kết cấu hay các quá trình, thực hiện tính toán dựa trên mô hình toán học và vật lý bằng các tính toán định lượng đối tượng được nghiên cứu khi thay đổi các tham số. Phương pháp này được áp dụng cho nhiều lĩnh vực từ vật lý, hóa học đến sinh học,…

Một trong những phương pháp thực nghiệm máy tính phổ biến nhất trên thế giới hiện nay là phương pháp Monte Carlo. Đây là một lớp các thuật toán sử dụng mẫu ngẫu nhiên để thu được kết quả số. Phương pháp này thường được sử dụng để giải quyết các bài toán có cấu hình phức tạp, liên quan đến nhiều biến số mà không dễ dàng giải quyết được bằng các thuật toán tất định. Có thể nói hiện nay phần lớn các sản phẩm của cả khoa học cơ bản lẫn ứng dụng đều dựa vào bộ ba thực nghiệm, lý thuyết và Monte Carlo [1], [3].

Phương pháp Monte Carlo mô hình hóa các hiện tượng tự nhiên thông qua việc mô phỏng trực tiếp các lý thuyết dựa theo yêu cầu của hệ thống, chẳng hạn như mô phỏng sự tương tác của những vật thể này với những vật thể khác hay với môi trường dựa trên các mối quan hệ vật thể - vật thể và vật thể - môi trường đơn giản. Lời giải được xác định bằng cách lấy mẫu ngẫu nhiên của các quan hệ này hoặc các tương tác vĩ mô, cho đến khi kết quả hội tụ. Do vậy, cách thực hiện lời giải này bao gồm các hành động hay phép tính được lặp đi lặp lại, có thể được thực hiện trên máy tính.

Do những ưu điểm trên, phương pháp Monte Carlo được ứng dụng trong nhiều lĩnh vực khác nhau: trong khoa học xã hội - phân luồng giao thông, nghiên cứu sự

phát triển dân số, nghiên cứu thị trường chứng khoán;…; trong khoa học tự nhiên - nghiên cứu sự vận chuyển bức xạ, thiết kế lò phản ứng hạt nhân, thiết kế vũ khí hạt nhân, tính liền bức xạ, sắc động học lượng tử, nghiên cứu sự chuyển pha, tính các tích phân số,…

b. Các phương pháp Monte Carlo

Sau hơn nửa thế kỷ phát triển, phương pháp Monte Carlo gần như đã được ứng dụng rộng khắp trên mọi lĩnh vực của khoa học, công nghệ. Cùng với đó, rất nhiều biến thể của phương pháp này được xây dựng nhằm phục vụ cho các nhu cầu tính toán cụ thể. Dưới đây là một số phương pháp tiêu biểu:

- Assorted random model: là thuật ngữ được dùng trong vật lý để mô tả một hệ động học có một điểm tới hạn như là một điểm thu hút. Do vậy các hoạt động vĩ mô của chúng được thực hiện trong không gian và thời gian đặc trưng bất biến của điểm tới hạn, tuy nhiên các điểm này được chỉ ra mà không cần đưa các thông số vào để đạt được giá trị chính xác. Nó được ứng dụng nhiều trong lĩnh vực khác như địa vật lý, vũ trụ học, sinh học, sinh thái học, kinh tế, xã hội học,…

- Phương pháp mô phỏng Monte Carlo trực tiếp (DSMC): được đưa ra bởi GS. Graeme Bird, đây là phương pháp sử dụng kỹ thuật mô phỏng xác suất để giải các phương trình Boltzman mô tả các dòng khí loãng mà trong đó quãng đường tự do trung bình của phân tử có cùng bậc (hoặc lớn hơn) thang chiều dài vật lý đặc trưng của hệ.

- Phương pháp Monte Carlo động lực (DMC): là phương pháp mô phỏng các trạng thái của phân tử bằng cách so sánh tỷ lệ của các bước riêng lẻ với các số ngẫu nhiên. Phương pháp DMC thường dùng để khảo sát các hệ thống không cân bằng chẳng hạn như các phản ứng, khuyếch tán,… Phương pháp này được ứng dụng chủ yếu để phân tích các hoạt động của các chất bị hút bấm trên các bề mặt.

Có nhiều phương pháp thông dụng sử dụng mô phỏng DMC như: First Reaction Method (FRM) và Random Seelection Method (RSM). Dù cho RFM và RSM đều cho ra kết quả giống nhau với cùng một mô hình, nhưng các tài nguyên máy tính khác nhau lại phụ thuộc vào hệ ứng dụng.

- Phương pháp Monte Carlo động học (KMC): là phương pháp Monte Carlo dựa trên sự mô phỏng máy tính để mô phỏng sự tiến triển theo thời gian của một vài quá trình xảy ra trong tự nhiên, điển hình là các quá trình mà chúng xuất hiện với một tỷ lệ được cho trước. Việc hiểu rõ các tỷ lệ này rất quan trọng vì chúng là dữ liệu đầu vào cho thuật toán KMC, tự bản thân phương pháp không thể dự đoán chúng.

Phương pháp KMC cũng rất giống với phương pháp DMC, sự khác biệt chính giữa chúng là thuật ngữ và lĩnh vực sử dụng: KMC được sử dụng chủ yếu trong vật lý còn DMC thì được sử dụng chủ yếu trong hóa học.

- Phương pháp Monte Carlo lượng tử (QMC): là phương pháp mô phỏng các hệ thống lượng tử với mục đích giải quyết các bài toán nhiều vật thể. QMC dùng phương pháp Monte Carlo bằng cách này hay cách khác để tính toán các tích phân nhiều chiều. QMC cho phép mô tả một cách trực tiếp các hiệu ứng nhiều vật thể trong hàm song, với độ bất định có thể được giảm với thời gian mô phỏng kéo dài.

- Phương pháp Quasi- Monte Carlo: là phương pháp tính toán tích phân (hay đôi khi là một bài toán) mà dựa trên cơ sở là các dãy số có sự nhất quán thấp. Nó trái ngược với phương pháp Monte Carlo thông thường được dựa trên các dãy số giả ngẫu nhiên.

c. Nền tảng của phương pháp Monte Carlo

Phương pháp Monte Carlo được xây dựng dựa trên các nền tảng sau:

- Các số ngẫu nhiên: đây là nền tảng quan trọng, góp phần hình thành nên “thương hiệu” của phương pháp. Các số ngẫu nhiên không chỉ được sử dụng trong việc mô phỏng lại các hiện tượng ngẫu nhiên xảy ra trong thực tế mà còn được sử dụng để lấy mẫu ngẫu nhiên của một phân bố nào đó, chẳng hạn như trong tính toán các tích phân số.

- Luật số lớn: luật này đảm bảo rằng khi ta chọn ngẫu nhiên các giá trị (mẫu thử) trong một dãy các giá trị (quần thể), kích thước dãy mẫu thử càng lớn thì các đặc trưng thống kê (trung bình, phương sai,…) của mẫu thử càng” gần” với các đặc trưng thống kế của quần thể. Luật số lớn nhất quan trọng đối với phương pháp

Xem tất cả 217 trang.