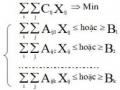Nguyên Tắc Hoạt Động Của Phương Pháp Monte Carlo [1]

Monte Carlo vì nó đảm bảo cho sự ổn định của các giá trị trung bình của các biến ngẫu nhiên khi số phép thử đủ lớn.

- Định lý giới hạn trung tâm: định lý này phát biểu rằng dưới một số điều kiện cụ thể, trung bình số học của một lượng đủ lớn các phép lặp của các biến ngẫu nhiên độc lập sẽ được xấp xỉ theo phân bố chuẩn. Do phương pháp Monte Carlo là một chuỗi các phép thử được lặp lại nên định lý giới hạn trung tâm sẽ giúp dễ dàng xấp xỉ được trung bình và phương sai của các kết quả thu được từ phương pháp.

Các thành phần chính của phương pháp Monte Carlo bao gồm:

- Hàm mật độ xác suất (PDF): một hệ vật lý (hay toán học) phải được mô tả bằng một bộ các PDF.

- Nguồn phát số ngẫu nhiên (RNG): một nguồn phát các số ngẫu nhiên đồng nhất phân bố trong khoảng đơn vị.

- Quy luật lấy mẫu: mô tả việc lấy mẫu từ một hàm phân bố cụ thể.

- Ghi nhận: dữ liệu đầu ra phải được tích lũy trong các khoảng giá trị của đại lượng cần quan tâm.

- Ước lượng sai số: ước lượng sai số thống kê theo số phép thử và theo đại lượng quan tâm.

- Các kỹ thuật giảm phương sai: các phương pháp nhằm giảm phương sai của đáp số được ước lượng để giảm thời gian tính toán của mô phỏng Monte Carlo.

- Song song hóa và vector hóa: các thuật toán cho phép phương pháp Monte Carlo được thực thi một cách hiệu quả trên một cấu trúc máy tính hiệu năng cao.

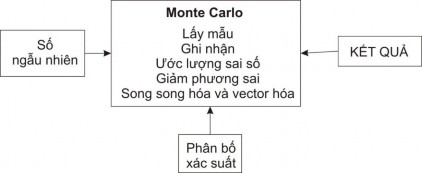
Hình 2.8. Nguyên tắc hoạt động của phương pháp Monte Carlo [1]

2.2.2.2. Mô phỏng sự phối hợp giữa máy xúc và ôtô bằng thuật toán Monte Carlo

a. Mô hình hoá toán học

Mô hình toán học mô phỏng sự phối hợp giữa máy xúc và ôtô được dựa trên sự phân tích các nhân tố điều khiển được và không điều khiển được, trong đó sự kết hợp các nhân tố điều khiển được sẽ đem lại hiệu quả kinh tế. Mô hình toán học của sự phối hợp này có thể biểu thị như sau [27]:

Hàm tối ưu Z = F( Xi, Yj) với: i = 1, 2…, M; j = 1, 2…, N (2.35)

Trong đó: Z - đánh giá hiệu quả (chi phí, lợi nhuận, năng suất...); Xi - các biến điều khiển được; Yj - các biến không điều khiển được; F - hàm điều khiển.

b. Phương pháp mô phỏng

Phương pháp mô phỏng được đưa ra dựa trên việc phân tích dữ liệu trực tiếp từ hệ thống. Với việc nghiên cứu 1 hệ thống vận tải riêng, giả sử xúc bốc và đổ thải được gắn với nhau thông qua tỷ lệ về sản lượng, Z được xác định là toàn bộ chi phí vận tải, Xi là biến điều khiển được (dạng vận tải, số lượng kích thước thiết bị,...), Yj là các biến không điều khiển được (sản lượng đề ra, các đặc điểm, các vị trí xúc bốc, đổ thải,...) thì việc lập kế hoạch quan tâm tới việc giảm tới mức tối thiểu chi phí vận tải với sản lượng xác định thông qua cách lựa chọn một hệ thống vận tải với kích cỡ và số lượng thiết bị trong hệ thống là tốt nhất.

c. Mẫu Monte Carlo

Mẫu Monte Carlo được xác định dựa trên ứng dụng của xác suất thống kê.

Việc xác định mẫu Monte Carlo được thực hiện theo quy trình sau [41]:

a. Tính xác suất của toàn bộ hàm F(x) của biến x trên miền (hình 2.9).

x

y = F(x) = f (x)dx



Trong đó: f(x) - Hàm tần số của x

b. Chọn một số bất kỳ, r giữa 0 và 1 từ bảng số ngẫu nhiên.

c. Từ xác suất toàn bộ hàm F(x), tìm giá trị x tương ứng với y = r.

(2.36)

Giá trị mô phỏng của x được phân phối theo tần số của hàm biến x. Các số liệu cho thấy rõ ràng xác suất có giá trị mô phỏng giữa x1 và x1 + dx có theo tỷ lệ f(x1)dx.

P(x1 < giá trị mô phỏng < x1 + dx) = dy1= f(x1)dx

x

Trong trường hợp biến bị dán đoạn, khi đó F(x) = f (u)

u 0

Trên hình 2.9 cho thấy: miền biến thiên của mẫu Monte Carlo sẽ tiến gần đến giá trị trung bình tiêu chuẩn và mẫu Monte Carlo trong nghiên cứu mô phỏng được xác định như trong bảng 2.4.

Hình 2.9. Miền biến thiên của mẫu Monte Carlo [41]

Bảng 2.4. Các biến số ngẫu nhiên tìm được theo các phân phối cơ bản [41]

Phân phối

Tham số	Trung bình	Biến đổi	Giá trị x theo biến ngẫu nhiên r	Ghi chú
Phân phối dạng hàm: f(x) = 1 ai < x < bi b a = 0 những số khác	a, b	a b 2	b a2 12	x = a + (b - a) r	0 ≤ r ≤ 1
Phân phối dạng hàm mũ: f(x) = αe-αt α > 0 , x ≥ 0	α	1 	1 2	x = 1 ln r 	0 ≤ r ≤ 1
Phân phối chuẩn: 1 1x 2 f(x) =e 2 x x 2x  -< x < 	μx , σx	μx	2 σx	12  x = xxri 6 i1 	0 ≤ ri ≤ 1

Có thể bạn quan tâm!

• Tổng Quan Về Một Số Thuật Toán Trong Nước Dùng Để Tính Toán Đồng Bộ Máy Xúc - Ôtô
• Sơ Đồ Chuyển Đổi Từ Trạng Thái Này Snag Trạng Thái Khác Của Tổ Hợp Ôtô - Máy Xúc [20] ‌
• Các Biến Điểm Trung Chuyển Và Thời Gian Di Chuyển Qua Các Điểm [6] ‌
• Nhóm Các Phương Pháp Sử Dụng Trí Tuệ Nhân Tạo:
• Đối Với Nhóm Các Phương Pháp, Thuật Toán Trong Nước Sử Dụng Để Tính Toán Sự Phối Hợp Giữa Máy Xúc – Ôtô:
• Các Yếu Tố Ảnh Hưởng Tới Hiệu Quả Phối Hợp Giữa Máy Xúc Và Ôtô Trên Các Mỏ Than Lộ Thiên Vùng Quảng Ninh

Xem toàn bộ 217 trang tài liệu này.

Phân phối kép:

f(x) = ncxPx(1 - P)n-x x = 0,1,2…n

P ≥ 0, P ≤ 1,0

n , p	np	np(1 - p)	ri ≤ pi , xi = xi-1 + 1 ri ≥ pi , xi = xi-1 xo = 0	0 ≤ ri ≤ 1
Phân phối Poisson: ex f(x) = x! x = 0,1,2,…: λ ≥ 0	λ	λ	λ	t i =  ln ri x x1 ti ≤ λ ≤ ti i0 i0	0 ≤ ri ≤ 1

d. Mô phỏng sự phối hợp giữa máy xúc và ôtô

Gọi M và N là số máy xúc và xe ôtô trong hệ thống, Cs là chi phí trong thời gian máy xúc chờ (đ/ph), Ct là chi phí thời gian xe ôtô chờ (đ/ph), Wm thời gian chờ tích lũy của máy xúc, Wn là thời gian chờ của xe ôtô, có các mối quan hệ:

Wm = F1(M, N)

Wn = F2(M, N) (2.37)

CT = Wm*Cs+ Ct

Trong đó: F1, F2 - hàm hệ thống; CT - tổng chi phí thời gian chờ.

Áp dụng thuật toán Monte Carlo tính toán mô phỏng đồng bộ máy xúc - ôtô cho các mỏ lộ thiên được thực hiện qua các bước như sau [2], [4]:

Bước 1: Gán các thông số đầu vào.

M, N - số máy xúc, số ôtô trong tổ hợp ĐBTB; Tni - thời gian chất tải của máy xúc thứ i, ph; ΔTn - độ lệch thời gian nhận tải, ph;

Thj - thời gian vận tải từ khi đi ra khỏi chỗ máy xúc của xe ôtô thứ j, ph; ΔTh - độ lệch thời gian vận tải, ph;

RNk - số ngẫu nhiên thứ k.

Bước 2: Tính thời gian chất tải cho máy xúc Tn = Tni + RNk*ΔTn

Bước 3: Tính thời gian di chuyển của các ôtô từ khi ra khỏi vị trí nhận tải: Th =Thj + RNk*ΔTh

Bước 4: Tính toán, phân tích trạng thái phối hợp của máy xúc và ôtô.

M - số máy xúc trong tổ hợp ĐBTB, chiếc; N - số ôtô trong tổ hợp ĐBTB, chiếc;

Txi - thời gian chạy của máy xúc thứ i, i = 1, 2 …, m; Toj - thời gian chạy của ôtô thứ j, j = 1, 2, 3…, n;

T - khoảng thời gian để ước lượng (tháng, năm,…). Quá trình tính toán diễn biến như sau:

Bước 4.a. Chọn ôtô với thời gian hoạt động nhỏ nhất (Tom) Đặt là ôtô thứ k với: Tom = Tok

Nếu Tok > T thì thực hiện bước 4.h.

Bước 4.b. Chọn máy xúc có thời gian hoạt động Txm nhỏ nhất, Đặt là máy xúc thứ g với: Txm = Txg

Bước4.c. Đặt w = (Txg - Tok)

- Nếu w < 0, thì thực hiện bước 4.d

- Nếu w > 0, thì thực hiện bước 4.e

- Nếu w = 0, ôtô được ấn định ngay cho máy xúc. Thực hiện bước 4.f. Bước 4.d. Máy xúc g đang đợi ôtô, thời gian chờ đợi của máy xúc là ws ws = (Tok - Txg)

Cập nhập trạng thái Txm của máy xúc g

Txg = Txg + ws Thực hiện bước 4.f

Bước 4.e. Ôtô k đang chờ nhận tải, thời gian chờ của ôtô k là wt wt = (Txg - Tok)

Cập nhập trạng thái Tok cho ôtô k Tok = Tok + wt

Bước 4.f. Đưa ra thời gian chất tải cho ôtô k bằng máy xúc thứ g, đặt là Lgk. Cập nhập trạng thái Txm của máy xúc và ôtô:

Txg = Txg + Lgk Tok = Tok + Lgk

Bước 4.g. Đưa ra thời gian di chuyển của ôtô thứ k từ nơi nhận tải tk. Cập nhập trạng thái Tok của ôtô thứ k.

Tok = Tok + Tk Thực hiện bước 4.a

Bước 4.h. Kết thúc mô phỏng kết thúc, xuất ra kết quả:

- Tổng khối lượng sản phẩm, tấn

- Số lượng chuyến vận chuyển, chuyến

- Thời gian chờ của mỗi ôtô ở từng máy xúc, ph

- Thời gian chờ của máy xúc với từng ôtô, ph.

Quá trình tính toán lựa chọn ĐBTB cho máy xúc và ôtô áp dụng thuật toán Monte Carlo được mô tả ở hình 2.10.

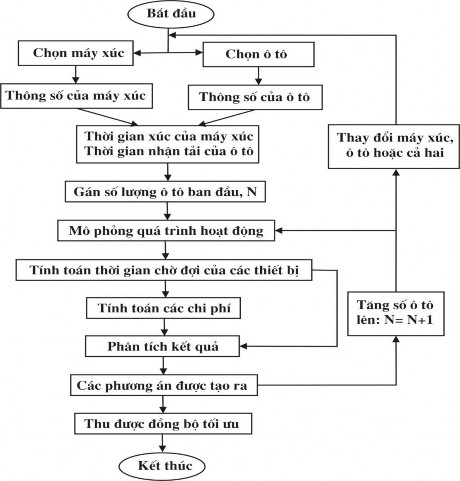
Hình 2.10. Sơ đồ khối mô phỏng quá trình lựa chọn ôtô [1, 3]

2.2.3. Nhóm các phương pháp dựa trên việc nghiên cứu các hoạt động của thiết bị trong đồng bộ:

Nhóm các phương pháp này bao gồm:

- Phương pháp qui hoạch tuyến tính [30], [36], [44];

- Phương pháp mô phỏng, [29], [43], [49], [50].

Các nghiên cứu điển hình theo phương pháp này là Rumfelt (1961), Stefako (1973), Learmont, Morgan (1975), Atkinson (1971, 1992), Singhal (1986), Lizotte,

Maehlmann (1988), Wiemer (1994), Vogt (1996),…

Xem tất cả 217 trang.