Kênh Mimo Trong Môi Trường Phản Xạ[1]

2.4. Mô hình kênh vật lý

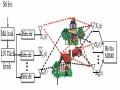
Mô hình toán học đã lý tưởng và trừu tượng hóa các kênh song song tương đương. Theo mô hình này muốn có đường truyền có thể hợp kênh tốt phải có hạng của ma trận kênh cao và số điều kiện tốt (chứ không phải là cứ có nhiều anten là tốt). Song trên thực tế đường truyền vật lý phải thỏa mãn điều kiện gì để đạt được các yêu cầu này. Chúng ta cũng tìm hiểu một số ví dụ đơn giản và phân tích hạng và các điều kiện ma trận kênh, tiền đề cho việc phân tích kênh MIMO thống kê. Để thuận tiện ta chỉ xét trường hợp các ăngten đặt thẳng hàng. Kết quả phân tích chi tiết phụ thuộc vào cấu trúc cụ thể từng trường hợp, tuy nhiên tư tưởng và phương pháp phân tích là như nhau.

2.4.1. Mảng ăngten nhìn thấy nhau (LOS)

[1] [Chúng ta hãy xét kênh MIMO trong điều kiện không có phản xạ hay nhiễu xạ, các dãy ăngten phát và thu đều được đặt thẳng hàng (hình 6), khoảng cách giữa các ăngten trong mảng phát và thu tương ứng là Δtλt và Δλc .

Anten ph¸ t k

t

t

Anten ph¸ t 1

Anten nhËn 1

d r

r

ircos r

kt cos t

Hình 6 Mô hình mảng ăngten nhìn thấy[1]

Hệ số kênh giữa ăngten phát k và ăngten thu i là:

hik

a exp(j2dik / c )

(2.17)

với dik là khoảng cách giữa 2 ăngten, a là hệ số suy giảm của môi trường được coi là như nhau cho các kênh truyền. Chúng ta cũng cho rằng kích thước các dãy

ăngten nhỏ hơn nhiều lần khoảng cách giữa 2 dãy ăngten này. Khoảng cách hai ăngten trong xấp xỉ bậc 1 cho bởi công thức:

dik

d  (i  1)r c cosr  (k  1)t c cost

(2.18)

ở đây d là khoảng cách giữa ăngten thu 1 và ăngten phát 1, r và t

là các góc tới từ

ăngten đến dãy ăngten kia. Đặt

t  cost ,

r  cosr

là cosin hướng của các góc

tới mảng phát và mảng thu thì công thức trên có thể đơn giản như sau [1]:

j2d 



hik

a exp

c

.exp( j2 (k  1)tt).exp( j2 (i  1)rr)



(2.19)

Ma trận kênh lúc này là:

j2d *

nt nr



H a

exp

c

er(r)et(t)



(2.20)

1 

Dù H có kích thước N x M nhưng nó chỉ có một giá trị riêng khác không

MN . Dung năng kênh truyền lúc này là:



Pa 2 MN 

M¶ng anten ph¸ t

C  log1





N0 

bits/s/Hz (2.21)



x

V*

U*

Có thể bạn quan tâm!

• Thuật toán d-blast trong công nghệ mimo - 1
• Thuật toán d-blast trong công nghệ mimo - 2
• Kỹ Thuật Hợp Kênh Không Gian (Spatial Multiplexage - Sm)
• Thuật toán d-blast trong công nghệ mimo - 5
• Thuật toán d-blast trong công nghệ mimo - 6

Xem toàn bộ 71 trang tài liệu này.

M¶ng anten thu

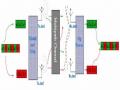
Hình 7 : Khối thể hiện kênh[1]

Phép phân tích ma trận H được minh họa trên hình 7. Mặc dù có nhiều ăngten phát và nhiều ăngten thu nhưng tất cả tín hiệu phát đều có cùng một chiều không gian (kênh chỉ có một mode riêng), do đó chỉ có bậc không gian tự do là 1.

Các tín hiệu đến ăngten thu có cùng hướng,

er (r ) . Do vậy bậc không gian tự do

không tăng cho dù số ăngten thu và phát đều tăng.

Thừa số MN đóng vai trò là hệ số công suất của kênh truyền MIMO. Nếu M

= 1 thì hệ số công suất đúng bằng số ăngten thu, và thu được bằng cách tổng hợp tỉ số cực đại tại bộ thu. Nếu N = 1 thì hệ số công suất bằng số ăngten phát, thu được bằng cách định dạng chùm tia phát. Nếu ta tăng số lượng cả ăngten thu và phát thì định dạng cả hai chùm tia thu-phát, tín hiệu phát được định dạng nội pha (in-phase) tại mỗi ăngten thu, sau đó các tín hiệu này lại được định dạng tổng hợp lại một lần nữa.

Sở dĩ như vậy là dù ma trận H có kích thước NxM nhưng vì kích thước mảng ăngten rất nhỏ so với khoảng cách thu phát nên các sóng tới ăngten gần như song song với nhau. Mỗi mảng ăngten nhiều phần tử tự nó đã tạo ra búp sóng nhận. Mọi tín hiệu đến trong phạm vi búp sóng đó thì đều coi là cùng một hướng. Mặc dù có nhiều ăngten phát nhưng vì khoảng cách rất xa nhau nên các tín hiệu đến mảng thu không thể đủ tách biệt về hướng để có thể làm tăng đáng kể dung năng của kênh truyền. Thực tế ma trận vẫn có hơn một giá trị đơn, nhưng đó là chưa đủ. Trong trường hợp này ma trận kênh H chỉ có một giá trị đơn thực sự, còn các giá trị đơn khác là rất nhỏ. Như đã phân tích ở trên, lúc này kênh chỉ có một mode riêng tốt, còn các mode khác là rất tồi.

Tóm lại trong môi trường không có vật cản, tức chỉ có tín hiệu trực tiếp từ ăngten phát đến ăngten thu, nếu khoảng cách thu phát rất lớn so với kích thước mảng ăngten, kênh MIMO chỉ làm tăng hệ số công suất chứ không làm tăng bậc không gian tự do.

2.4.2. Kênh MIMO với một đường phản xạ

[1]Chúng ta có thể tạo ra kênh truyền tốt như trường hợp trên mà không cần phải đặt các ăngten xa nhau. Trong trường hợp này, ngoài một đường trực tiếp từ ăngten phát đến ăngten thu, ta còn có một đường khác do phản xạ trên vật cản (chẳng hạn bức tường). Gọi tín hiệu trực tiếp là 1, tín hiệu phản xạ là 2. Tín hiệu i sẽ có độ suy giảm ai và góc với dãy ăngten phát φti (Ωti = cos φti ), góc với dãy ăngten thu là φri (Ωri = cos φri ). Chúng ta hãy tìm điều kiện của tia phản xạ để có thể đạt được mục đích này.

D· y anten ph¸ t

D· y anten thu

A

path 2

Anten ph¸ t 1

t1

t2

path 1

r2

B

r1

Anten thu 1

(a)

D· y anten ph¸ t

D· y anten thu

A

B

H'

H"

(b)

Hình 8 Kênh MIMO trong môi trường phản xạ[1]

Một cách trực quan có thể coi tín hiệu từ ăngten phát đến ăngten thu qua một trạm trung gian AB như trên hình 2.8a. Lúc này kênh MIMO với bức tường phản xạ được chia thành 2 kênh nối tiếp H’ và H’’(hình 8b). H’ chính là ma trận của kênh có 2 ăngten thu đặt xa nhau, H’’ là ma trận kênh có 2 ăngten phát đặt xa nhau:

e* ( ) 

H '' abe ( ), a be (

),

H ' t1 t1 

(2.22)

1 r r1 2 r r 2

e* ( )

t 2

b j2d i 

t 2 



với , ai

ai

MN exp

C

, (2.23)



di là khoảng cách giữa ăngten phát thứ nhất và ăngten thu thứ nhất của tín hiệu thứ i.

Ma trận kênh MIMO lúc này sẽ là tích của hai ma trận trên, H = H’’H’

H abe ( )e *abe ( )e (

)* , với i = 1, 2 (2.24)

i r r1 t t1 2 r r 2 t t 2

b j2d i 



và , ai

ai

MN exp

c

,



(2.25)

i

d là khoảng cách giữa ăngten phát thứ nhất và ăngten thu thứ nhất. Nếu

t1

t 2

mod 1

t

và r1

r 2

mod 1

r

(2.26)

thì cả hai ma trận H’ và H’’ đều đạt được điều kiện tốt sẽ có hạng 2, tất nhiên lúc này mà trận H cũng sẽ có hạng 2. Tham số quyết định hiệu quả hoạt động của kênh chính là Lr Ωr và Lt Ωt.

Kênh MIMO với đường phản xạ tương tự như 2 kênh truyền phân tập ở đầu thu và đầu phát. Mặc dù các ăngten thu và phát được đặt sát nhau nhưng vẫn đạt được sự tách biệt về không gian. Hiệu ứng phản xạ cung cấp nguồn thu ảo và phát ảo. Kênh từ mảng phát ảo cũng như kênh từ mảng thu ảo đều có hạng 2 nên kênh tổng hợp cũng vậy, tức có hợp kênh không gian. Trong trường hợp này fading đa đường trở nên có lợi.

Một chú ý quan trọng trong ví dụ trên là góc tới của 2 tia ở cả ăngten thu và phát quyết định điều kiện tốt của ma trận H. Điều này không có được ở một số môi trường. Ví dụ, nếu vật phản xạ ở gần ăngten phát hơn thì góc Ωr sẽ rất nhỏ, nếu nó ở gần ăngten thu hơn thì góc Ωt sẽ rất nhỏ (hình 8). Trong cả hai trường hợp trên H đều không đạt được điều kiện tốt. Như vậy điều kiện tốt trong trường hợp kênh MIMO có một đường phản xạ yêu cầu góc tới giữa tín hiệu trực tiếp và phản xạ không được quá nhỏ.

Kh¸ c biÖt gãc nhËn lí n

D· y anten

nhËn

Kh¸ c biÖt gãc ph¸ t nhá

D· y anten ph¸ t

(a)

D· y anten

ph¸ t

D· y anten nhËn

(b)

Hình 9 Các vật phản xạ gần ăngten thu hơn (a) và gần ăngten phát hơn (b).[1]

Thật may là trong nhiều ứng dụng không phải cả ăngten phát và thu đều nhỏ.Trong hệ thống điện thoại tế bào, khi các trạm cơ sở được đặt trên các toà nhà cao tầng thì vật phản xạ ở rất gần máy di động, nhưng vẫn có được hợp kênh không gian khi các ăngten trạm cơ sở được đặt xa nhau.

Kết qủa sẽ không thay đổi nếu môi trường là phản xạ và tán xạ cao. Trong trường hợp này hiện tượng đa đường trở lên có lợi và không thể thiếu để tăng dung năng kênh truyền. Hầu hết các ứng dụng của chúng ta đều nằm trong điều kiện này, do đó kênh MIMO trở lên rất hữu hiệu để nâng cao tốc độ dữ liệu, đáp ứng nhu cầu ngày càng cao trong thông tin vô tuyến hiện nay.

Có sự khác biệt giữa mô hình toán học và mô hình vật lý của kênh MIMO. Trong mô hình toán học chỉ cần ma trận kênh có hạng cao là có thể có thể phân tích kênh MIMO thành n kênh song song. Mô hình vật lý đòi hỏi ngoài điều kiện ma trận có hạng cao thì các giá trị đơn của nó không được quá khác biệt.

2.5. Dung năng kênh fading

Kênh fading là kênh có hệ số truyền hij (m) thay đổi ngẫu nhiên theo một hàm phân bố nào đó (Điển hình là Rayleigh hay Rice). Xét biểu diễn tín hiệu băng cơ sở phức của một kênh song song fading phẳng (bỏ qua chỉ số i,j)

y[m]=

h[m]x[m]+ [m]

(2.27)

với {h[m]} là quá trình fading với chuẩn hóa

E[ | h[m]|2 ]= 1 và {[m]} là ồn i.i.d

CN(0, N0). Đặc tính của fading là có thể làm kênh suy giảm sâu với xác suất cao dẫn đến thay đổi khái niệm dung năng kênh theo ý nghĩa cổ điển là một giới hạn trên xác định của tốc độ truyền tin cậy. Tuy nhiên với fading nhanh, hệ số kênh có thể được lấy trung bình hóa và bảo toàn được khái niệm dung năng theo ý nghĩa là đại lượng trung bình. Với fading chậm dung năng được mở rộng sang một khái niệm mới là dung năng dừng kênh (outage capacity)

2.5.1 Kênh fading nhanh

Đấy là kênh có fading thay đổi nhanh đến mức nó có thể trải qua tất cả các trạng thái fading (các giá trị phân bố có thể) trong khoảng thời gian truyền một từ mã. Tức là trễ truyền cho phép lớn hơn thời gian kết hợp kênh và từ mã có thể chịu tất cả các trạng thái fading dẫn đến việc có thể lấy trung bình dung năng kênh.

Để cụ thể, ta xét mô hình kênh fading nhanh đơn giản [1]:

y[m]=

h[m]x[m]+ [m]

(2.28)

với

h[m]=

hl được giữ không đổi trên khoảng thời gian kết hợp Tc thứ l của kí

hiệu và là i.i.d trên các khoảng thời gian kết hợp khác nhau. Trên khoảng L thời gian kết hợp, nếu Tc>>1, ta có thể coi rằng kênh truyền này gồm có L kênh truyền con song song độc lập với nhau về mức độ thăng giáng. Xác suất dừng kênh từ L kênh này là:

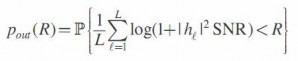
(2.29)

với L hữu hạn. Đại lượng:

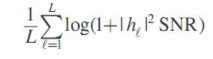
(2.30)

là ngẫu nhiên và có một xác suất khác không mà tốc độ sẽ sụt giảm xuống dưới tốc độ đích R. vì thế, sẽ không có khái niệm dung năng theo nghĩa là tốc độ cực đại mà tốc độ truyền dưới nó có thể cho độ tin cậy tùy ý truyền thống nên ở đây phải sử dụng đến khái niệm dừng kênh. Tuy nhiên, khi L → ∞, thì

(2.31)

Tức là chúng ta có thể lấy trung bình trên nhiều kênh truyền độc lập thăng giáng bằng cách mã hóa trên một số lượng lớn các khoảng thời gian kết hợp và mức độ

tin cậy truyền thông dưới tốc độ của

E[log(1+ | h |2 SNR)]

có thể thực sự đạt được.

Trong trường hợp này, sẽ rất có ý nghĩa để đưa ra dung năng cho kênh fading nhanh, dùng cho trường hợp bộ thu biết kênh truyền:

C = E[log(1+ | h |2 SNR)] bit/s/Hz (2.32)

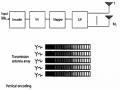
kênh fading nhanh khi bên phát không biết kênh (không thể dùng thuật toán đổ nước) thuật toán chia đều công suất tổng bị giới hạn cho các kênh song song tương đương (khi SNR cao) cũng cho phép đạt dung năng kênh MIMO là thuật toán V- Blast.

2.5.2 Kênh fading chậm

[1]Xét trường hợp hệ số kênh truyền ngẫu nhiên nhưng thay đổi chậm theo thời gian, ví dụ h[m]=h với nhiều m mà trễ truyền lại yêu cầu nhỏ hơn thời gian kết hợp của kênh truyền. Điều này có nghĩa là từ mã chỉ chịu một trạng thái kênh ngẫu nhiên cụ thể mà không chịu tất cả các trạng thái ngẫu nhiên của kênh. Do đó ta không thể thực hiện phép lấy trung bình trạng thái kênh. Mô hình này gọi là kênh fading chậm

Giả sử h là số thực, ngoài ra kênh có ồn AWGN với SNR. Tín hiệu bên thu là

|h|2SNR. Tốc độ cực đại của truyền tin tin cậy hỗ trợ bởi kênh truyền này là log(1+|h|2SNR) bit/s/Hz. Đại lượng này là một hàm số của hệ số kênh truyền ngẫu nhiên h nên nó cũng là ngẫu nhiên. Cho rằng tốc độ mã hóa tại nơi phát là R

Xem tất cả 71 trang.