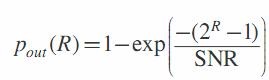bit/s/Hz. Nếu như kênh truyền thực có giá trị h suy giảm đến mức log(1+|h|2SNR)
pout (R) := P{log(1+|h|2SNR) < R} (2.33) vì thế, nơi phát có thể mã hóa dữ liệu tốc độ mong muốn R khi hệ số kênh truyền đủ mạnh để hỗ trợ tốc độ đó. Truyền thông tin cậy có thể đạt được bất cứ lúc nào nếu không xảy ra hiện tượng dừng kênh. Dễ hiểu hơn là kênh truyền có hệ số fading h cho phép dữ liệu đi qua với tốc độ cự đại là log(1+|h|2SNR) bit/s/Hz. Quá trình giải mã tin cậy khi giá trị này vượt quá tốc độ dự định R. Có thể bạn quan tâm! Xem toàn bộ 71 trang tài liệu này. Hình 10 Mật độ của log(1+|h|2SNR), cho Rayleigh fading và SNR=0dB. Với tốc độ đích R, sẽ có một xác suất dừng kênh khác không[1] Với kênh Rayleigh fading (có h chuẩn hóa là CN(0, 1)), xác suất dừng kênh với tốc độ truyền R sẽ là: tại SNR cao: p (R) » (2R - 1) (2.34) (2.35) và xác suất này giảm theo 1/SNR. out SNR Chúng ta thấy rằng việc mã hóa không thể cải thiện đáng kể xác suất lỗi trong kênh fading chậm. Nguyên nhân là do trong khi mã hóa có thể lấy trung bình ồn Gauss, thì nó lại không thể lấy trung bình đối với kênh truyền fading chậm và điều này tác động tới tất cả các từ được mã hóa. Vì thế với hiện tượng kênh có hệ số thăng giáng sâu, lỗi đặc trưng xuất hiện cả khi mã hóa hoặc không mã hóa. Đây là khái niệm khác nhau giữa kênh AWGN và kênh fading chậm. Trong những kĩ thuật trước đây, một bên có thể phát đi luồng dữ liệu có tốc độ xác định (chỉ cần nhỏ hơn dung năng) với xác suất lỗi có thể nhỏ tùy ý. Điều này là không thể có trên kênh fading chậm khi mà xác suất kênh truyền ở trong trạng thái giảm sâu là khác không. Tức là ở mọi tốc độ truyền (kể cả xấp xỉ bằng không) không thể mã cho lỗi nhỏ tùy ý mà phải chấp nhận xác xuất lỗi khác không tương ứng với tốc độ đó khi xảy ra dừng kênh. Vì thế, một đại lượng thay thế được đưa ra là dung năng dừng kênh : Đó là tốc độ truyền lớn nhất Cε khi mà xác suất dừng kênh nhỏ hơn ε: C= log(1+ F- 1(1- )SNR) bit/s/Hz (2.36) với F ở đây là hàm phân phối tích lũy bù của |h|2: F (x):= P{| h |2>x} Tóm lại: Trong kênh fading nhanh thuật toán mã kênh nhằm đạt tốc độ truyền cao nhất (đạt tới dung năng) có xác suất lỗi nhỏ tùy ý. Còn trong kênh fading chậm thuật toán mã kênh là nhằm đạt xác suất dừng kênh nhỏ nhất với tốc độ truyền lựa chọn trước. Điều này sẽ dẫn đến thuật toán D-Blast là một trong các kỹ thuật đạt được điều này 2.6 Kỹ thuật Hợp kênh không gian (Spatial multiplexage - SM) Để thực hiên được hệ thống hợp kênh không gian, khai thác hết các tính chất phân tập của kênh MIMO nhằm tạo tốc độ truyền tin cao nhất trên cùng một băng tần, bên kênh 2 kỹ thuật chia thành các luồng song song ở bên phát cố định đến từng anten (V-Blast) hay quét lần lượt trên các anten phát, rất quan trọng là kỹ thuật thu làm sao tách các tín hiệu chồng chập trên một anten thu thành các luồng song song như bên phát. Ở đây ta phân tích các nguyên tắc thu và tách tín hiệu cơ bản trong hệ MIMO. 2.6.1 Giải mã hợp lý cực đại. Ta nhắc lại rằng trong mô hình SISO Truyền thống. Nguyên tắc quyết định được dùng là nguyên tắc quyết định theo xác suất khả năng cực đại (Maximumlikelihood). Tức là điểm tín hiệu nhận được sẽ được quyết định là điểm chòm sao gần nhất trong bảng chòm sao của bên phát. (khoảng cách gần nhất ứng với xác suất lớn nhất). Do đó bên phát có nhiệm vụ dò tìm khoảng cách nhỏ nhất, tức là phải tính tất cả các khoảng cách từ điểm tín hiệu nhận được đến tất cả các điểm tín hiệu trên chòm sao để tìm ra điểm có khoảng cách nhỏ nhất. Kỹ thuật này khó được áp dụng trong hệ thống MIMO, vì mỗi thành phần của vecto nhận (giả sử số anten phát và thu bằng nhau và bằng nt=nr=n) sẽ phải dò tìm điểm trên chòm sao của nó, và giả sử các chòm sao đều có số điểm là M, thì sô phép tính khoảng cách để sau đó tìm ra tập điểm có khoảng cách với vecto nhận được nhỏ nhất là Mn (tức là số phép tính tăng theo hàm mũ). Điều này sẽ làm chậm đáng kể tốc độ truyền cho dù đó là các đường truyền song song. Biểu diễn toán học của bộ thu ML đối với hệ MIMO : y = Hx + w (2.37) là bộ giải mã hợp lý cực đại tìm từ mã x$thỏa mãn: x$ argminTr yx.H H.yx.H (2.38) x Do độ phức tạp tính toán trên mà bộ thu hay dùng các thuật toán giải mã phân lớp (V-Blast hay D-Blast) chuyển số phép toán tính khoảng để dò tìm về n.M khoảng cách để đảm bảo tốc độ truyền dẫn nhanh. Để tìm hiểu các thuật toán phân lớp này trước hết ta đưa ra các định nghĩa về các phép toán cơ bản 2.6.2 Phép toán ép về không (Zero-forcing) Là phép toán nhân vecto nhận được với ma trận nghịch đảo kênh. Một kênh ISI có thể xem tương đương như một bộ lọc đáp ứng xung hữu hạn (FIR) cộng với ồn. Bộ cân bằng ZF sử dụng bộ lọc đảo (sau khi ước lượng kênh) để bù lại hàm đáp ứng kênh. Đầu ra của bộ cân bằng ZF làm đáp ứng bằng 1 với ký hiệu mong được tách, và đáp ứng 0 cho các ký hiệu còn lại không mong muốn. Điều này sẽ giúp loại bỏ hoàn toàn giao thoa từ các ký hiệu khác , hay tách được sự chồng chập giữa các ký hiệu. Tuy nhiên ZF chỉ làm việc tốt khi hệ thống cân bằng tuyến tính không có ồn. Vì thực tế ồn có thể tăng lên khi áp dung phép toán ZF Để chỉ ra ý tưởng chủ đạo và ứng dụng của nó vào hệ thống của chúng ta, giả thiết rằng số ănten thu bằng số ănten phát nt nr và H là ma trận vuông hạng đầy đủ. Trong trường hợp này thì ma trận đảo của ma trận H là tồn tại. Chúng ta có: y . H-1 x w . H-1 (2.39) Ồn ở đây vẫn là ồn Gauss và ký hiệu thứ n có thể được giải mã bằng cách tìm các điểm gần chòm sao nhất để thu được n thành phần của y.H-1 . Tuy nhiên, công suất của ồn lúc này là w.H1 có thể lớn hơn công suất của ồn ban đầu w. Nếu số ănten phát và thu không bằng nhau chúng ta có thể nhân (2.39) với ma trận nghịch đảo Moore–Penrose suy rộng. Trên cơ sở phân tích. H=U..V H Ở đây Ma trận cơ sở U và Vcó kích thước tương ứng nt xnt và nr xnr và (2.40) Σ là một ma trận nt xnr với các thành phần j , j , j = 1, 2, . . . , nt, j là trị riêng j thứ j của H.HH . Các cột của U là các véc tơ riêng của H.HH , trong khi các cột của V là các véc tơ riêng của HH .H . Chúng ta giả thiết rằng r là hạng của H, tương đương với hạng của H.HH . Không mất tính tổng quát chúng ta giả thiết rằng các trị riêng không tăng tuần tự. Nghịch đảo Moore–Penrose suy rộng của H là: H+ V U H , (2.41) Ở đây là chuyển vị của Σ trong đó j , j , j = 1, 2, . . . , r được thay thế bởi 1/ j, j . Chú ý rằng H là vuông và không suy biến chúng ta có H+ H-1 và thu được kết quả giống như trước. Nếu nt xnr thì H là hạng đầy đủ, chúng ta có H+ HH .(H.HH )1 . chính bởi vậy nhân (2.39) với y.H+ x.H.HH .(H.HH )1 w.H+ x+w.H+ H+ thu được: (2.42) Tóm lại là nếu không có ồn và nếu ước lượng được chính xác ma trận kênh H, thì ta có thể tìm được ma trận nghịch đảo (hay nghịch đảo mở rộng) để tìm được chính xác vécto tín hiệu bên phát (trung với các điểm trên các chòm sao), song do có ồn nên các điểm biến đổi ngược bị sai lệch đi (sự sai lệch còn bị tăng thêm đo ma trận nghịch đảo) * Ví dụ 1:[12] Xét một kênh MIMO có (M,N) = (3,4) với chòm sao 16-QAM có các điểm là: A = {±1±j, ±1±j3, ±3±j, ±3±j3} Chuẩn hóa công suất ồn N0=1 và cho Eb/N0 = 2.5. Giả sử ma trận kênh H là: 0 0.7i 0.3 0.3i 0.5 0.4i H 0.8 0.6i 0.7 1.1i 0.8 1.1i 0.8 0i 0.2 0.3i 0 0.2i 0.1 0.2i 1.2 0.3i 1.7 0.6i Còn vec tơ tín hiệu gửi đi là x = (1+i, -1-i, 1+3i)T, và kênh cộng thêm vectơ ồn w=(0.6 + 0.4i, 0.4 - 0.1i, 0.7 + 0.5i, 0.2 - 0.2i)T sẽ cho vectơ tín hiệu thứ y là: y = Hx + w = 1.5 2.2i 2.4 2.8i 0.4 0.6i 1.1 7i Ma trận khả nghịch H+ được tính theo công thức H+ HH .(H.HH )1 như sau: 0.2 0.7i H 0.5 0.2i 0.2 0.1i 0.7i 0.8 0.4i 0.5 0.3i 0.2 0.2i 0.2 0.5i 0.4 0.1i 0.3 0.4i 0.5 0.0i 0.7 0.2i Ta có ma trận H+H là: 1 0 H H 0 1 0 0 0 0 1 Lối ra bộ ước lượng ZF xˆZF được tính như sau: 0.2 1.1i xˆ H y 0.6 0.1i ZF 1.6 3.6i Khi chúng ta gán xˆZF thành các kí hiệu 16-QAM gần nhất, chúng ta thu được vectơ quyết định như sau: 1ixˆ 1i 1 3i vectơ này không cho ta ước lượng chính xác của x (do sai khác thành phần đầu tiên so với x ban đầu). Trong ví dụ này bộ thu ZF loại trừ hoàn toàn các nhiễu đồng kênh khi có điều kiện H+H=I (thể hiện tính trực giao của 2 ma trận). Song các bộ thu ZF lại cho phản hồi công suất ồn mạnh, điều này có thể thấy rõ vì tỉ số tín trên ồn tại lối vào bộ ước lượng ZF là: SNRZF ,in 5.03 Hx 2 w 2 trong khi SNR lối ra của bộ ước lượng ZF là: SNRZF ,out H w 2 H Hx 2 x 2 H w 2 4.41 Chúng ta thấy rằng có sự giảm giá trị của SNR là do tăng cường nhiễu, tỉ số: SNRZF ,out SNRZF ,in 0.88 1 2.6.3. Phép toán tối thiểu trung bình bình phương lỗi (MMSE) Là phép toán nhân vectơ nhận được với ma trận (dạng của nó có được trên cơ sở để có một ước lượng với chỗ sai khác với các điểm đúng của chòm sao tối thiểu, hay đạo hàm của hàm lỗi theo các hệ số của ma trận nhân bằng zero ). Như đã nói ở trên, cân bằng ZF làm tăng ồn. Mục đích của phép toán cân bằng MMSE tuyến tính là nhân phương trình hệ MIMO với một ma trận để ảnh hưởng của ồn được tối thiểu. Nói một cách tương đương, bộ cân bằng MMSE tối đa hóa tỷ số SNR. Giả sử xˆMMSE là kết quả sau khi nhân ma trận này xˆMMSE trong đó Z được chọn để cực tiểu hoá: Zy Zy x 2 (2.43) (2.44) Đối với mô hình kênh này, trong đó H và w là Gauss, thì ma trận ước lượng MMSE như sau: Z M H ( M HH N I )1 (2.45) 0 N trong đó: ρ ES N0 là toán tử kỳ vọng được sử dụng trong trường hợp này vì kênh là ngẫu nhiên. Để làm sáng tỏ phép tính này ta xét lại ví dụ 1 *Ví dụ 2: [12] Sử dụng kênh như trong ví dụ 1 với các giá trị H, x, w và N0 như cũ. Ở đây, 10 M và ma trận MMSE được kết qủa như sau: 0.2 0.5i Z 0.3 0.1i 0.1 0.1i 0.0 0.6i 0.6 0.3i 0.4 0.2i 0.1 0.2i 0.2 0.4i 0.2 0.1i 0.2 0.3i 3 0.0i 0.5 0.1i Lối ra bộ ước lượng xˆMMSE được tính là: 0.1 1.1i xˆ Zy - 0.4 - 0.4i MMSE 1.4 3.2i Do vậy, vectơ quyết định của bộ ước lượng MMSE là: 1i xˆ 1i, đây là ước lượng 1 3i chính xác của x.Bộ ước lượng MMSE không loại trừ hoàn toàn nhiễu đồng kênh vì: 0.6 0.2i 0.1 0.1i ZH 0.2i 0.6 0.1 0.2i 0.1 0.1i 0.1 0.2i 0.7 không bằng ma trận đồng nhất, không giống như trường hợp của bộ ước lượng ZF. Song bộ ước lượng MMSE có ưu điểm là nhiễu không mạnh như bộ ước lượng ZF. Điều này có thể thấy được bằng cách tính các tỉ số SNR đầu vào và đầu ra của bộ ước lượng MMSE: SNRMMSE,in 5.03 Hx 2 w 2 SNRMMSE ,out Chúng ta có tỉ số giữa các SNR như sau: ZHx 2 Zw 2 27.56 SNRMMSE ,out SNRMMSE ,in 5.48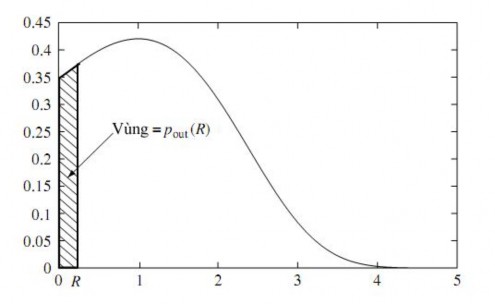
 Thuật toán d-blast trong công nghệ mimo - 1
Thuật toán d-blast trong công nghệ mimo - 1 Thuật toán d-blast trong công nghệ mimo - 2
Thuật toán d-blast trong công nghệ mimo - 2![Kênh Mimo Trong Môi Trường Phản Xạ[1]](https://tailieuthamkhao.com/uploads/2022/05/15/thuat-toan-d-blast-trong-cong-nghe-mimo-3-120x90.jpg) Kênh Mimo Trong Môi Trường Phản Xạ[1]
Kênh Mimo Trong Môi Trường Phản Xạ[1] Thuật toán d-blast trong công nghệ mimo - 5
Thuật toán d-blast trong công nghệ mimo - 5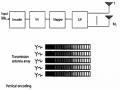 Thuật toán d-blast trong công nghệ mimo - 6
Thuật toán d-blast trong công nghệ mimo - 6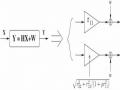 Thuật toán d-blast trong công nghệ mimo - 7
Thuật toán d-blast trong công nghệ mimo - 7