cùng kênh tần số hoặc thời gian khi sử dụng nhiều ăngten tại cả máy phát lẫn máy thu trong lĩnh vực phát thanh, tuy nhiên dưới đây sẽ điểm lại các sự kiện lịch sử phát triển hệ thống MIMO theo 2 góc độ kỹ thuật: Phân tập theo không gian (Spatial diversity) và ghép kênh theo không gian (Spatial multiplexing).
1.2.1 Phân tập không gian
Năm 1991: Kỹ thuật phân tập trễ (Delay diversity) được phát minh bởi Wittneben
Năm 1998: Kỹ thuật phân tập dùng Mã hoá không gian - thời gian mắt cáo STTC (Space – Time Trellis Coding) của Tarokh.
Năm 1999: Alamouti giới thiệu kỹ thuật Mã hoá không gian - thời gian khối STBC (Space – Time Block Coding).
1.2.2 Ghép kênh theo không gian
Năm 1994: Paulraj & Kailath giới thiệu kỹ thuật phân chia mặt đất (Ground breaking results), nêu ra khái niệm hợp kênh không gian với Patent US năm 1994 nhấn mạnh việc ứng dụng cho phát thanh quảng bá.
Năm 1996: Foschini giới thiệu kỹ thuật BLAST (Bell Labs Layered Space Time) nhằm hợp các luồng truyền song song trên kênh fading nhanh. Cũng thời gian này Foschini cùng Greg Raleigh đã tạo ra phương pháp mới về công nghệ có khả năng tăng hiệu suất thực về sử dụng kênh, được cấp bản quyền phát minh Mimo OFDM khi cho ra đời chipset “Pre _N” có tên là True MiMo.
Năm 1997: Winter trình bày các kết quả nghiên cứu tổng quát đầu tiên về dung năng kênh MIMO, chứng minh tiềm năng phát triển của nó.
Có thể bạn quan tâm!
-
 Thuật toán d-blast trong công nghệ mimo - 1
Thuật toán d-blast trong công nghệ mimo - 1 -
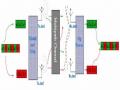
![Kênh Mimo Trong Môi Trường Phản Xạ[1]](data:image/svg+xml,%3Csvg%20xmlns=%22http://www.w3.org/2000/svg%22%20viewBox=%220%200%2075%2075%22%3E%3C/svg%3E) Kênh Mimo Trong Môi Trường Phản Xạ[1]
Kênh Mimo Trong Môi Trường Phản Xạ[1] -
 Kỹ Thuật Hợp Kênh Không Gian (Spatial Multiplexage - Sm)
Kỹ Thuật Hợp Kênh Không Gian (Spatial Multiplexage - Sm) -
 Thuật toán d-blast trong công nghệ mimo - 5
Thuật toán d-blast trong công nghệ mimo - 5
Xem toàn bộ 71 trang tài liệu này.
Năm 1998 sản phẩm mẫu hợp kênh đầu tiên cho tốc độ truyền dẫn cao được làm bởi Bell labs
Năm 2001 sản phẩm thương mại đầu tiên của hãng Iospan Wireless Inc dùng công nghệ MIMO-OFDMA hỗ trợ cả mã phân tập và hợp kênh không gian.
Năm 2006 một số công ty Broadcom, Intel.. đưa ra giải pháp MIMO-OFDM theo chuẩn IEEE 802.11n. Cũng trong thời gian này Beceem Commmnications, Samsung,.. cũng phát triển MIMO-OFDMA dựa trên IEEE 802 16e là WIMAX. Tất cả đi đến hệ thống 4G đều dùng công nghệ MIMO.
Điểm lại các sự kiện lịch sử như vậy để thấy rằng lý thuyết cũng như công nghệ MIMO mới được phát triển đột phá trong hơn thập kỷ qua nhằm tăng tốc độ và độ tin cậy trên đường truyền vô tuyến vốn chịu nhiều tác động của can nhiễu và bị giới hạn lý thuyết ở mức thấp theo công thức Shannon (1948) cổ điển. Dưới đây luận văn sẽ trình bày mô hình hệ thống MIMO tổng quát sau đó tập trung phân tích riêng về thuật toán D-Blast cho kênh fading chậm.
Chương II Mô hình hợp kênh không gian hệ thống MIMO
2.1 Mô tả hệ thống
Hình 2 diễn tả mô hình hệ thống thông tin vô tuyến MIMO.
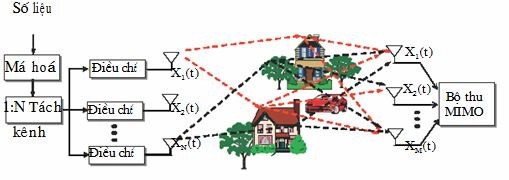
Hình 2 : Cấu trúc hệ thống thông tin vô tuyến Mimo
Trong hệ thống MIMO nhằm tăng tốc độ truyền, dòng dữ liệu bên phát được tách thành N dòng số liệu song song có tốc độ thấp hơn (dòng con). N chính là số anten phát. Mỗi một dòng số liệu có tốc độ thấp sẽ được điều chế và phát đi trên mỗi anten phát. Thông thường các máy phát sẽ làm việc ở cùng một tốc độ, tuy nhiên tốc độ này có thể được điều chỉnh linh hoạt theo yêu cầu và dịch vụ bằng phương pháp điều chế thích ứng. Các dòng số liệu lúc này có tốc độ chỉ bằng 1/N tốc độ dòng số liệu ban đầu, được phát đồng thời trên cùng một băng tần, nên về mặt lý thuyết hiệu suất sử dụng phổ sẽ tăng lên gấp N lần. Các tín hiệu được phát đồng thời qua kênh vô tuyến trên cùng một phổ tần và được thu bởi M ăngten của hệ thống thu.
Bằng phương pháp truyền dẫn này, hiệu suất sử dụng phổ có thể sẽ tăng theo hàm tuyến tính với số anten là min(M,N), so với việc tăng theo hàm loga của hệ thống phân tập hay không phân tập truyền thống. Hệ thống MIMO chỉ có hiệu suất sử dụng phổ cao khi hệ thống làm việc được trong môi trường kênh giầu tán xạ (scattering). Các dòng dữ liệu từ các anten phát qua kênh chồng chập lên nhau ở các anten thu sẽ hoàn toàn được phân tách trở lại bằng các thuật toán ở bên thu. Điều này thực hiện được khi các đường truyền riêng rẽ giữa hệ thống phát và hệ thống thu không tương quan với nhau do có sự khác nhau về tham số không gian
và đường truyền tán xạ. Hệ thống máy thu có thể sử dụng sự khác biệt về tham số không gian này để tách các tín hiệu có cùng tần số được phát đồng thời từ các anten khác nhau.
2.2. Mô hình toán học
r t
[1] [Chúng ta bắt đầu từ trường hợp đơn giản là kênh truyền có hệ số truyền xác định (không có fading mà chỉ có hệ số suy giảm và ồn) và được biết trước (qua phép ước lượng kênh), băng tần hẹp bất biến với thời gian. Hệ thống có nt ănten phát nr ănten thu có thể được biểu diễn qua ma trân kênh Hn xn sẽ có mô tả toán học
là:
y = Hx + w (2.1)
r
trong đó x Cntlà véc tơ bên phát (gồm ntký hiệu từ ntanten phát), y Cnrlà nr giá trị nhận được tại nranten thu, w CN(0, N0In) là ồn trắng Gauss tại một thời
điểm kí hiệu. Ma trận kênh H Cnrxnt
được coi là xác định và không đổi trong thời
gian truyền, được biết ở cả bên thu và phát, hij là hệ số suy giảm kênh từ ănten phát j đến ănten thu i, tổng công suất phát của các anten giới hạn là P.
Ta sẽ phân tích kênh ma trận này thành các kênh vô hướng độc lập song song. Như đã biết trong đại số tuyến tính, mọi phép biến đổi tuyến tính đều có thể thực hiện qua 3 bước: phép quay, phép tỉ lệ, và phép quay ngược. Ma trận H có phép phân tích giá trị riêng (singular value decomposition SVD) như sau:
H = U V* (2.2)
với U Cntxnt, V Cnrxnr
là các ma trận đơn vị, R nr xnt
là ma trận chữ nhật có
các phần tử trên đường chéo là thực không âm, các phần tử còn lại bằng 0. Các phần tử trên đường chéo được sắp xếp là 1 2 … nmin là các giá trị đơn (singular values) của ma trận H, nmin := min(nt, nr). Từ
HH* = Ut (2.3)
ta có i2 là giá trị riêng (eigenvalues) của ma trận HH* và cũng là của ma trận H*H, và chỉ có nmin giá trị riêng. Chúng ta có thể viết lại phép phân tích H theo SVD như tổng các ma trận hạng bậc 1:
nmin
H =
u v * (2.4)
i1
i i i
Hạng của ma trận H đúng bằng số các giá trị riêng khác không. Đặt:
~x = V*x, (2.5)
y~= U*y, (2.6)
w~= U*w, (2.7)
khi đó công thức (2.1) có thể viết lại như sau:
y~= ~x + w~(2.8)
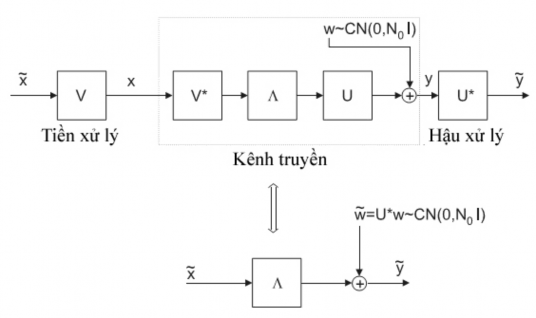
Hình 3: Phép biến đổi SVD biến kênh ma trận thành các kênh song song [1] dễ thấy w~và w có cùng hàm phân bố, || ~x ||2= ||x||2.
Như vậy với giới hạn năng lượng cho trước, kênh Gauss vectơ có thể biểu diễn tương đương dưới dạng nmin kênh Gauss vô hướng song song:
y
~ii~xiw~i
với i=1,2,…nmin (2.9)
Phép biến đổi được minh hoạ trên hình 3.
Phép phân tích SVD được minh hoạ thông qua 2 phép chuyển tọa độ tín hiệu vào được chuyển sang cơ sở là các cột của V, và tín hiệu ra chuyển sang cơ sở là
các cột của U thì mối liên hệ giữa tín hiệu ra - vào rất đơn giản: phép tỉ lệ theo hệ số λi. Phương trình (2.9) biểu diễn kênh MIMO (2.1) trong mỗi quan hệ mới.
Khi đó dung năng của kênh ma trận sẽ là tổng dung năng của các kênh truyền song song tương đương. Với công suất tổng cộng giới hạn, việc phân tách công suất theo thuật toán đổ nước sẽ làm cực đại tổng dung năng:
nmin
C = log( 1 +
i1
* 2
P
i i
N 0
) bits/s/Hz (2.10)
Với Pi* là công suất phân bố theo kiểu đổ nước:
N
P* 0(2.11)
i 2
i
được chọn sao cho thỏa mãn điều kiện ràng buộc công suất tổng:
i
P* P . (2.12)
i
Ở đây kí hiệu x+ := max (x,0).
Mỗi giá trị riêng λi tương ứng với chế độ riêng của kênh, còn gọi là kênh riêng. Mỗi kênh riêng khác không có thể hỗ trợ một luồng dữ liệu. Do vậy, kênh MIMO có thể hỗ trợ đa thành phần không gian của nhiều luồng dữ liệu.
2.3 Hạng và điều kiện số
[1]Trong một số trường hợp theo thuật toán đổ nước, các kênh con có đáy ở trên mặt nước và nó không được mang tí công suất nào (hình 5). Đây là kênh quá tồi để có thể truyền tải thông tin. Thông thường công suất phát sẽ được phân bố nhiều cho kênh có hệ số cao để tận dụng điều kiện kênh tốt, và rất ít thậm chí là không cho kênh yếu. Do đó, tại SNR cao, mức nước là sâu, tiệm cận tối ưu đạt được khi công suất phân đều lên các kênh con:
k P2 k 2
C log1 i k log SNR log i
bit/s/Hz (2.13)
i 1
kN0
i 1
k
với k là số giá trị riêng i2 khác không và là hạng của ma trận H,
và SNR := P/N0 . Và khi đó C sẽ tỷ lệ tuyến tính theo k Mặt khác theo bất đẳng thức Jensen:
k
1 k P 2
P 1 k 2
klog1kN
i log1kN i
(2.14)
Và vì:
i 1
0
0 i 1
k
2 Tr[HH*] h 2
(2.15)
i
i1
ij
i, j
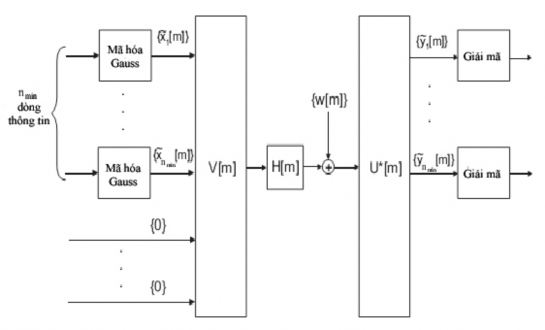
Hình 4: Cấu trúc SVD của kênh MIMO[1]
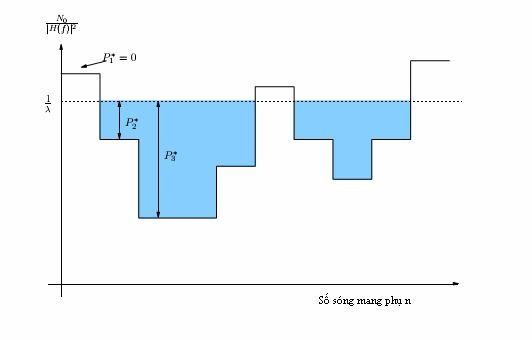
Hình 5: Phân bố công suất theo thuật toán đổ nước[1]
Nên có thể nói rằng trong các kênh ma trận có cùng hệ số công suất tổng cộng, kênh có dung năng cao nhất khi tất cả các giá trị riêng bằng nhau.
Tổng quát hơn là kênh nào các giá trị riêng tập trung hơn (ít sai khác giữa giá trị lớn nhất và nhỏ nhất), kênh đó có dung năng lớn hơn trong chế độ SNR cao. Theo phân tích này tỷ số max λi/minλi được định nghĩa như là điều kiện số của ma trận H (diễn tả độ tập trung của giá trị đơn). Tức là kênh ma trận có điều kiện tốt khi có hạng cao và điều kiện số gần đến 1.
Trường hợp SNR thấp, dung năng phụ thuộc chủ yếu vào kênh riêng mạnh
nhất:
C P max 2log e
i
2
bits/s/Hz (2.16)
N 0i
Trong chế độ này hạng hay điều kiện số của ma trận kênh là ít liên quan. Tóm lại, theo mô hình toán học, hạng ma trận kênh và độ phân tán các giá trị riêng là tham số quan trọng quyết định hiệu quả hoạt động của kênh. Trong điều kiện SNR cao, dung năng sẽ cực đại nếu các công suất phát phân chia đều trên các angten.


![Kênh Mimo Trong Môi Trường Phản Xạ[1]](https://tailieuthamkhao.com/uploads/2022/05/15/thuat-toan-d-blast-trong-cong-nghe-mimo-3-120x90.jpg)