các giả thuyết trở thành rỗng, thì ta kết luận giả thuyết ban đầu là đúng với phép thế biến θ.
Sau đây là thủ tục suy diễn lùi. Trong thủ tục này, Hyp và θ là các biến địa phương trong thủ tục. Giá trị ban đầu của Hyp là danh sách các giả thuyết ban đầu (biểu diễn câu hỏi được đặt ra), còn giá trị ban đầu của θ là phép thế rỗng.
Input: Cơ sở trí thức (FB, RB), Giả thuyết Hyp.
Output: Kết luận Hyp là đúng và đưa ra phương pháp lập luận θ hoặc Hyp không đúng.
Procedure Backward_Chaining (Hyp, θ) Begin
H ← giả thuyết đầu tiên trong danh sách Hyp; for mỗi luật R = (Conds, Q) do
Begin
if H hợp nhất với Q bởi phép thế θ1 then
1. Loại H khỏi danh sách Hyp;
2. Thêm các điều kiện của luật Conds vào danh sách Hyp;
3. Áp dụng phép thế θ1 vào các giả thuyết trong danh sách Hyp;
4. Lấy hợp thành của các phép thế θ và θ1 để nhận được phép thế θ mới, tức là θ ← θθ1;
if Hyp = [ ] then cho ra θ
else Backward_Chaining (Hyp, θ); End;
End;
Trong thủ tục lập luận lùi, mỗi θ được cho ra là một phép thế biến làm cho giả thuyết ban đầu trở thành đúng, tức là (Hyp) θ = H1θ...Hmθ là đúng (là hệ quả logic của CSTT). Do đó mỗi phép thế biến θ được cho ra bởi thủ tục là một câu trả lời cho câu hỏi đặt ra.
Ví dụ 5.11:
Cho trước các sự kiện: A (1)
B (2)
và các luật:
R1: A C (3)
R2: B D (4)
R3: C E (5) R4: A D E (6) R5: B C F (7) R6: E F G (8)
Chứng minh G.
Xét giả thuyết Hyp={G} (9) Từ (8), (9) suy ra Hyp={E, F} (10)
Từ (7), (10) suy ra Hyp={E, B, C} (11)
Từ (11), (5) suy ra Hyp={B, C} (12)
Từ (12), (2) suy ra Hyp={C} (13)
Từ (13), (3) suy ra Hyp={A} (14)
Từ (14), (1) suy ra Hyp=[] Vậy G được chứng minh.
Ví dụ 5.12: Cho các biểu thức logic sau: AC (1)
AB F (2)
(D B) F I (3)
HAF (4)
FGH I (5)
ADC (6)
AD GH (7)
Chứng minh I bằng lập luận lùi trên hệ luật Horn.
Giải:
- Bước 1: Chuyển các luật về dạng câu Horn
+ Xét (1) suy ra A, C
+ Xét (2) đã có dạng Horn
+ Xét (3) (DF) (BF) I
((DF) (BF)) I
((DF) (BF)) I
((DF) I) ((BF) I)
((DF) I) ((BF) I) suy ra DFI, BF I
+ Xét (4): HAF
(HA) F
HAF
+Xét (5) đã có dạng Horn
+Xét (6): Tương tự như (4), ta có (6) (ACD)
+ Xét (7) ta có AD GH suy ra AD G và ADH (luật loại khỏi hội) Vậy ta có:
(8) | |
C | (9) |
AB F | (10) |
DFI | (11) |
BF I | (12) |
HAF | (13) |
FGH I | (14) |
ACD | (15) |
AD G | (16) |
ADH | (17) |
Có thể bạn quan tâm!
-
 Một Cây Chứng Minh Từ Đồ Thị Phân Giải Trong Hình 4.2
Một Cây Chứng Minh Từ Đồ Thị Phân Giải Trong Hình 4.2 -
 Biểu Diễn Tri Thức Bằng Mạng Ngữ Nghĩa
Biểu Diễn Tri Thức Bằng Mạng Ngữ Nghĩa -
 Nhập môn trí tuệ nhân tạo - 20
Nhập môn trí tuệ nhân tạo - 20 -
 Các Kiểu Dữ Liệu Sơ Cấp Của Prolog
Các Kiểu Dữ Liệu Sơ Cấp Của Prolog -
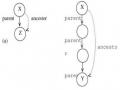
 Các Cặp Tổ Tiên Hậu Duệ Gián Tiếp Ở Các Mức Khác Nhau
Các Cặp Tổ Tiên Hậu Duệ Gián Tiếp Ở Các Mức Khác Nhau -
 Mô Hình Vào/ra Của Một Thủ Tục Thực Hiện Một Danh Sách Các Đích
Mô Hình Vào/ra Của Một Thủ Tục Thực Hiện Một Danh Sách Các Đích
Xem toàn bộ 272 trang tài liệu này.
Bước 2: Sử dụng lập luận lùi với Hyp=[I] (18)
- Xét (18), (11) Hyp={D, F} (19)
- Xét (19), (15) Hyp={A, C, F} (20)
- Xét (20), (13) Hyp={A, C, H} (21)
- Xét (21), (17) Hyp={A, C, D} (22)
- Xét (22), (15) Hyp={A, C} (23)
- Xét (23), (8), (9) Hyp=[]
Kết luận: I được chứng minh.
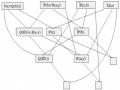
Ví dụ 5.13. Xét cơ sở luật trong sở thú (đã đề cập trong mục 5.3.1) Luật 1: longmao(x) covu(x) (1)
Luật 2: longvu(x) chim(x) (2)
Luật 3: bietbay(x) detrung(x) chim(x) (3)
Luật 4: covu(x) anthit(x) thuanthit(x) (4)
Luật 5: covu(x) rangnhon(x) mongvuot(x) thuanthit(x) (5) Luật 6: thuanthit(x) vanghung(x) domsam(x) baochauphi(x) (6) Luật 7: thuanthit(x) vanghung(x) vanden(x) ho(x) (7) Luật 8: chim(x) bietbay(x) chandai(x) codai(x) dadieu(x) (8)
Luật 9: chim(x) bietbay(x) bietboi(x) dentrang(x) canhcut(x) (9) Giả sử có cơ sở sự kiện sau:
(10) | |
Chandai(BiBi) | (11) |
codai(BiBi) | (12) |
bietbay(BiBi) | (13) |
Xét giả thuyết Hyp={dadieu(BiBi) } (14)
(14) hợp nhất được với dadieu(x) trong (8) bởi phép thế [x/BiBi], do đó: Hyp={bietbay(BiBi), chandai(BiBi), codai(BiBi), chim(BiBi) } (15)
Xét (15) khớp với (13) Hyp={chandai(BiBi), codai(BiBi), chim(BiBi) } (16) Xét (16) khớp với (11) Hyp={codai(BiBi), chim(BiBi) } (17)
Xét (17) khớp với (12) Hyp={chim(BiBi) } (18)
Xét (18) khớp với (2) bởi phép thế [x/BiBi] Hyp={longvu(BiBi) } (19) Xét (19) khớp với (10) Hyp=[]
Kết luận: Giả thiết"BiBi là đà điểu"là đúng.
Ví dụ 5.14. Giả sử CSTT bao gồm:
- Cơ sở luật gồm 2 luật sau:
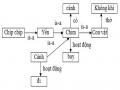
Nếu (x là ngựa) và (x là mẹ của y) và (y chạy nhanh) thì x có giá Nếu z thắng cuộc thì z chạy nhanh.
- Cơ sở sự kiện gồm các sự kiện sau: Tom là ngựa
Ken là ngựa Kit là ngựa Bin là ngựa
Tom là mẹ của Bin Tom là mẹ của Ken Bin là mẹ của Kit. Kit chạy nhanh.
Bin thắng cuộc.
Hỏi: con ngựa nào có giá. Trả lời:
Định nghĩa các vị từ sau:
- Horse(x) (x là ngựa),
- Mother(x, y) (x là mẹ của y),
- Fast(y) (y chạy nhanh),
- Winner(x) (x thắng cuộc). CSTT được miêu tả như sau: Horse(Tom) (1)
Horse(Ken) (2)
Horse(Kit) (3)
Horse(Bin) (4)
Mother(Tom, Bin) (5)
Mother(Tom, Ken) (6)
Mother(Bin, Kit) (7)
Fast(Kit) (8)
Winner(Bin) (9)
Horse(x) Mother(x, y) Fast(y) ⇒ Valuable(x) (10) Winner(z) ⇒ Fast(z) (11)
Chú ý rằng các sự kiện từ (1) đến (9) có thể coi như các luật đặc biệt với điều kiện=.
Giả thuyết ban đầu Hyp = [Valuable(w)] và θ = []. Giả thuyết Valuable(w) hợp nhất được với kết luận của luật (10) bởi phép thế θ1 = [w/x], do đó ta nhận được danh sách các giả thuyết mới
Hyp = [House(x), Mother(x, y), Fast(y)] và θ = θθ1 = [w/x]
a) Trường hợp 1:
Giả thuyết House(x) hợp nhất được với sự kiện (1) bởi phép thế θ1 = [x/Tom], ta nhận được danh sách các giả thuyết mới
Hyp = [Mother(Tom, y), Fast(y) ] và θ = [w/x][x/Tom] = [w/Tom]
Giả thuyết Mother(Tom, y) hợp nhất được với sự kiện (5) bởi phép thế θ1 = [y/Bin], ta nhận được danh sách các giả thuyết Hyp = [Fast(Bin) ]
và θ = [w/Tom][y/Bin] = [w/Tom, y/Bin]
Giả thuyết Fast(Bin) hợp nhất được với kết luận của luật (11) bởi phép thế [z/Bin], do đó ta có Hyp = [Winner(Bin) ]
và θ = [w/Tom, y/Bin, z/Bin]
Giả thuyết Winner(Bin) trùng với sự kiện (9) (hợp nhất được bởi phép thế θ1 = []). Do đó danh sách các giả thuyết trở thành rỗng với phép thế θ = [w/Tom, y/Bin, z/Bin].
Như vậy với phép thế này thì giả thuyết Valuable(w) trở thành đúng, hay nói cách khác, Tom là con ngựa có giá.
b) Trường hợp 2:
Giả thuyết House(x) hợp nhất được với sự kiện (4) bởi phép thế θ1 = [x/Bin], ta nhận được danh sách các giả thuyết mới
Hyp = [Mother(Bin, y), Fast(y) ] và θ = [w/x][x/Bin] = [w/Bin]
Giả thuyết Mother(Bin, y) hợp nhất được với sự kiện (7) bởi phép thế θ1 = [y/Kit], ta nhận được danh sách các giả thuyết Hyp = [Fast(Kit) ]
và θ = [w/Bin][y/Kit] = [w/Bin, y/Kit].
Giả thuyết Fast(Kit) trùng với sự kiện (8) (hợp nhất được bởi phép thế θ1 = []). Do đó danh sách các giả thuyết trở thành rỗng.Vậy Bin là con ngựa có giá.
c) Các trường hợp còn lại: thực hiện tương tự khi hợp nhất House(x) với phép thế [x/Ken] hoặc [x/Kit] đều không dẫn đến danh sách các giả thuyết trở thành rỗng.
Kết luận: Tom và Bin là hai con ngựa có giá.
5.4. Lập trình Prolog
5.4.1. Giới thiệu ngôn ngữ Prolog
Prolog là ngôn ngữ lập trình logic. Ngôn ngữ Prolog do giáo sư người Pháp Alain Colmerauer và nhóm nghiên cứu của ông đề xuất lần đầu tiên tại trường Đại học Marseille đầu những năm 1970. Đến năm 1980, Prolog nhanh chóng được áp dụng rộng rãi ở châu Âu, được người Nhật chọn làm ngôn ngữ phát triển dòng máy tính thế hệ 5. Prolog đã được cài đặt trên các máy vi tính Apple II, IBM-PC, Macintosh.
Prolog còn được gọi là ngôn ngữ lập trình ký hiệu (symbolic programming) tương tự các ngôn ngữ lập trình hàm (functional programming), hay lập trình phi số (non- numerical programming). Prolog rất thích hợp để giải quyết các bài toán liên quan đến các đối tượng (object) và mối quan hệ (relation) giữa chúng.
Prolog được sử dụng phổ biến trong lĩnh vực trí tuệ nhân tạo. Nguyên lý lập trình logic dựa trên các mệnh đề Horn (Horn logíc). Một mệnh đề Horn biễu diễn một sự kiện hay một sự việc nào đó là đúng hoặc không đúng, xảy ra hoặc không xảy ra.
Ví dụ 5.15: Sau đây là một số mệnh đề Horn:
1. Nếu một người già mà (và) khôn ngoan thì người đó hạnh phúc.
2. Jim là người hạnh phúc.
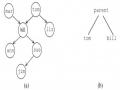
3. Nếu X là cha mẹ của Y và Y là cha mẹ của Z thì X là ông của Z.
4. Tom là ông của Sue.
5. Tất cả mọi người đều chết (hoặc Nếu ai là người thì ai đó phải chết).
6. Socrat là người.
Trong các mệnh đề Horn ở trên, các mệnh đề 1, 3, 5 được gọi là các luật (rule), các mệnh đề còn lại được gọi là các sự kiện (fact). Một chương trình logic có thể được xem như là một cơ sở dữ liệu gồm các mệnh đề Horn, hoặc dạng luật, hoặc dạng sự kiện, chẳng hạn như tất cả các sự kiện và luật từ 1 đến 6 ở trên. Người sử dụng (NSD) gọi chạy một chương trình logic bằng cách đặt câu hỏi (query/ question) truy vấn trên cơ sở dữ liệu này, chẳng hạn câu hỏi:
Socrat có chết không?
(tương đương khẳng định Socrat chết đúng hay sai?)
Một hệ thống logic sẽ thực hiện chương trình theo cách"suy luận"-tìm kiếm dựa trên vốn"hiểu biết"đã có là chương trình - cơ sở dữ liệu, để minh chứng câu hỏi là một khẳng định, là đúng (Yes) hoặc sai (No). Với câu hỏi trên, hệ thống tìm kiếm trong cơ sở dữ liệu khẳng định Socrat chết và"tìm thấy"luật 5 thoả mãn. Vận dụng luật 5, hệ thống nhận được Socrat là người chính là sự kiện 5. Từ đó, câu trả lời sẽ là: Yes có nghĩa sự kiện Socrat chết là đúng.
5.4.2. Cú pháp Prolog
a) Các thuật ngữ
Một chương trình Prolog là một cơ sở dữ liệu gồm các mệnh đề (clause). Mỗi mệnh đề được xây dựng từ các vị từ (predicat). Một vị từ là một phát biểu nào đó về các đối tượng có giá trị chân đúng (true) hoặc sai (fail). Một vị từ có thể có các đối là các nguyên logic (logic atom).
Mỗi nguyên tử (nói gọn) biểu diễn một quan hệ giữa các hạng (term). Như vậy, hạng và quan hệ giữa các hạng tạo thành mệnh đề.
Hạng được xem là những đối tượng"dữ liệu"trong một trình Prolog. Hạng có thể là hạng sơ cấp (elementary term) gồm hằng (constant), biến (variable) và các hạng phức hợp (compound term).
Các hạng phức hợp biểu diễn các đối tượng phức tạp của bài toán cần giải quyết thuộc lĩnh vực đang xét. Hạng phức hợp là một hàm tử (functor) có chứa các đối (argument), có dạng:
Tên_hàm_tử(Đối_1,..., Đối_n)
Tên hàm tử là một chuỗi chữ cái và/hoặc chũ số được bắt đầu bởi một chữ cái thường. Các đối có thể là biến, hạng sơ cấp, hoặc hạng phức hợp. Trong Prolog, hàm tử đặc biệt "."(dấu chấm) biểu diễn cấu trúc danh sách (list). Kiểu dữ liệu hàm tử tương tự kiểu bản ghi (record) và danh sách (list) tương tự kiểu mảng (array) trong các ngôn ngữ lập trình mệnh lệnh (C, Pascal...).
Ví dụ 5.16: f(5, a, b).
student(robert, 1975, info, 2, address(6, 'mal juin', 'Caen')). [a, b, c]
Mệnh đề có thể là một sự kiện, một luật (hay quy tắc), hay một câu hỏi. Prolog quy ước viết sau mỗi mệnh đề một dấu chấm để kết thúc như sau:
• Sự kiện: <... >.
(tương ứng với luật <... >:- true.)
• Luật: <... >:- <... >.
• Câu hỏi?- <... >.
(ở chế độ tương tác có dấu nhắc lệnh)
b) Các kiểu dữ liệu Prolog
Prolog có kiểu dữ liệu sơ cấp và kiểu dữ liệu có cấu trúc. Sự phân lớp này nhận biết kiểu của một đối tượng nhờ bề ngoài cú pháp.
Cú pháp của Prolog quy định mỗi kiểu đối tượng có một dạng khác nhau. Prolog không cần cung cấp một thông tin nào khác để nhận biết kiểu của một đối tượng. Trong Prolog, NSD không cần khai báo kiểu dữ liệu.

Hình 5.2. Các kiểu dữ liệu trong Prolog
Các kiểu dữ liệu Prolog được xây dựng từ các ký tự ASCII:
• Các chữ cái in hoa A, B,..., Z và chữ cái in thường a, b,..., z.
• Các chữ số 0, 1,..., 9.
• Các ký tự đặc biệt, chẳng hạn + - * / < > =:. & _ ~.
c) Chú thích
Trong một chương trình Prolog, chú thích (comment) được đặt giữa hai cặp ký hiệu /* và */ (tương tự ngôn ngữ C). Ví dụ:
/*************************/
/*** Đây là một chú thích ***/
/*************************/