Automat Hữn Hạn Đơn Định Đoán Nhận Ngôn Ngữ L

2.1.4. Sự tương đương giữa DFA và NFA

Mỗi DFA là một NFA đặc biệt, nên rò ràng lớp ngôn ngữ được đoán nhận bởi NFA cũng bao gồm các tập chính quy (đây chính là ngôn ngữ được đoán nhận bởi DFA ). Tuy nhiên, không có cơ sở để nói rằng NFA chỉ đoán nhận duy nhất các tập hợp này. Điều đó cho thấy DFA có thể mô phỏng được hoạt động của NFA, nghĩa là với mỗi NFA, ta có thể xây dựng một DFA tương đương (đoán nhận cùng một ngôn ngữ với nó). Để một DFA mô phỏng được hoạt động của NFA ta cho các trạng thái của DFA tương ứng với tập các trạng thái của NFA. Tại mỗi thời điểm, DFA lưu giữ trong bộ điều khiển tất cả các trạng thái mà NFA có thể chuyển đến khi đọc cùng một ký hiệu vào như DFA.

1) Định lý

Giả sử L(M) là ngôn ngữ đoán nhận bởi Automat hữu hạn không đơn định M, khi đó sẽ tồn tại Automat hữu hạn đơn định M‟ đoán nhận L(M) hay nói cách khác L(M) = L(M‟).

Chứng minh:

Giả sử cho M = <Q, , , q0, F> là Automat không đơn định, ta xây dựng Automat M‟= <Q‟, , ‟, q‟0, F‟> như sau:

- Q‟ = {[U]U  Q; U ≠ } (Q‟ là tập tất cả các tập con khác rỗng của Q).

Tại mỗi thời điểm, M‟ sẽ lưu giữ trong trạng thái của nó tất cả các trạng thái có thể có của M. Một trạng thái trong Q‟ là ký hiệu là [q1, q2, ..., qi] trong đó {q1, q2,

..., qi } là một tập con của Q. Ta coi [q1, q2,..., qi] là một trạng thái đơn của automat

M‟ và nó tương ứng với một tập trạng thái của automat hữu hạn không đơn định M.

- q‟0 = [q0]; q‟0 là tập con của Q có một phần tử q0.

- F‟ = U]  Q U  F , F‟ là tập các tập con của Q giao với F khác rỗng hay F‟ là tập hợp các trạng thái của Q‟ có chứa ít nhất một trạng thái kết thúc trong tập F của M.

- Ánh xạ ‟ được xây dựng bằng cách dựa vào  như sau:

‟: Q‟  Q‟ xác định như sau:

δ‟(U, a) = δ‟( [q1, q2,..., qi ], a) = [p1, p2,..., pj ] = V

 δ ({q1, q2,..., qi }, a) = {p1, p2,..., pj}

Hay ‟ (U, a) = V = q  U (q, a) với U, V  Q‟ và a

Rò ràng với cách xây dựng như trên thì M‟ là Automat hữu hạn đơn định.

Bây giờ ta chứng minh quy nạp theo độ dài của xâu vào w rằng:

δ‟(q‟0 , w) = [q1, q2,..., qi ]  δ(q0, w) = {q1, q2,..., qi} (1) Với w = 0 , ta có w = ε và q‟0 = {q0} nên (1) hiển nhiên đúng

Giả sử (1) đúng với các xâu vào w có độ dài tới m.

Xét xâu vào có độ dài m + 1, đặt xâu này là wa với a  Σ, ta có: δ‟(q‟0, wa) = δ‟(δ‟(q‟0, w), a)

Theo định nghĩa hàm chuyển δ‟, ta có: δ‟([q1, q2,..., qi ], a) = [p1, p2,..., pj ]

 δ ({q1, q2,..., qi }, a) = {p1, p2,..., pj}

Mặt khác theo giả thiết quy nạp δ‟(q‟0, w) = [p1, p2,..., pj ]

 δ(q0, w) = {p1, p2,..., pj}

Nên thay vào ta có δ‟(q‟0, wa) = [r1, r2,..., rk ]

 δ(q0, wa) = {r1, r2,..., rk}.

Dễ thấy rằng δ‟(q‟0, w)  F‟  δ(q0, w)  F .

Vậy L(M) = L(M‟).

Từ định lý, ta có giải thuật chuyển NFA về DFA.

2) Giải thuật chuyển NFA về DFA

Input: NFA M = <Q, , , q0, F>

Output: DFA M‟ = <Q‟, ‟, ‟, q‟0, F‟>; L(M) = L(M‟)

Process:

- Q‟ = { [U]U  Q; U ≠ };

- q‟0 = [q0];

- ‟= ;

- F‟ = [U]  Q‟ U  F ;

- ‟: Với mỗi [U]  Q‟ thực hiện Với mỗi a ‟ tính

δ‟([U], a) = δ‟( [q , q ,..., q ], a) = δ ({q , q ,..., q }, a)

1 2 i 1 2 i

q U (q , a) = {p , p ,..., p }

i i 1 2 j

= [p , p ,..., p ] = V.

1 2 j

Hay ‟ (U, a) = V

Ví dụ:

1. Cho NFA: M = <Q, , , q0, F>, trong đó:

- Q = {q , q };

0 1

-  {0, 1};

- q  q

0 0

- F = {q };

1

- δ:

∅

δ(q , 0) = {q , q }; δ(q ,1) = {q }; δ(q , 0) = ; δ(q , 1) = {q , q }.

0 0 1 0 1 1 1 0 1

Biểu diễn M bằng đồ thị:

Start

q0

0

q1

1

0 1

1

Hình 2.9. Đồ thị của NFA

Biểu diễn M bằng bảng:



Q

0	1
q 0	{q ,q } 0 1	{q } 1
q 1		{q ,q } 0 1

Có thể bạn quan tâm!

• Văn Phạm Chính Quy Và Automat Hữu Hạn
• Biểu Diễn Automat Bằng Đồ Thị
• Automat Hữu Hạn Không Đơn Định-Nfa (Nondeterministic Finite Automata)
• Sự Tương Đương Giữa Nfa Có Và Không Có Ε-Dịch Chuyển
• Một Số Tính Chất Đại Số Của Biểu Thức Chính Quy
• Sự Tương Đương Giữa Văn Phạm Chính Quy Và Automat Hữu Hạn

Xem toàn bộ 254 trang tài liệu này.

Bảng 2.8. Bảng chuyển trạng thái

Ta xây dựng DFA tương đương M‟ = <Q‟, ‟, δ‟, q‟0, F‟) đoán nhận L(M) như sau:

- Q‟: chứa tất cả các tập con của Q = {q0, q1};

Vậy Q‟ = {[q0], [q1], [q0, q1]}; đặt A = [q0], B = [q1], C = [q0, q1];

- ‟=  = {0, 1};

- q‟0 = [q0] = A;

- F‟ = {[q1], [q0, q1]} = {B, C}

- Hàm chuyển δ‟:

δ‟(q‟0, 0) = δ‟([q0], 0)

 δ‟(A, 0) = δ(q0, 0) = [q0, q1] = C

Tương tự: δ‟(A, 1) = B;

δ‟(B, 0) = ∅;

δ‟(B, 1) = C;

Cuối cùng: δ‟(C, 0) = C vì

δ‟(C, 0) = δ‟([q0, q1], 0) = δ({q0, q1},0) = δ(q0, 0)  δ(q1, 0)

= {q0, q1} ∅ = [q0, q1] = C.

δ‟(C, 1) = C vì

δ‟(C, 1) = δ‟([q , q ], 1) = δ({q , q }, 1) = δ(q , 1)  δ(q , 1)

0 1 0 1 0 1

= {q }  {q , q } = [q , q ] = C.

1 0 1 0 1

Biểu diễn M‟ bằng đồ thị:

Start

A

0

C

1

1

B

0

1

Hình 2.10. Biểu diễn M’ bằng đồ thị

Biểu diễn M‟ bằng bảng:

‟

Q‟

0	1
A	C	B
B		C
C	C	C

Bảng 2.9. Biểu diễn M’ bằng bảng

2. Cho M = < Q, , , q0, F >;

Trong đó: - Q = {q0, q1, q2};

-  = {0, 1};

- F = { q2};

- q0 = q0;

: (q0, 0) = {q0, q1};

(q1, 1) = {q2};

(q2, 1) = {q2}.

Biểu diễn M bằng đồ thị:

Start

q0

0

q1

1

q2

0

1

Hình 2.11. Biểu diễn M bằng đồ thị

Biểu diễn M bằng bảng:



Q

0	1
q 0	{q ,q } 0 1
q 1		{q } 2
q 2		{q } 2

Bảng 2.10. Biểu diễn M bằng bảng

Automat trên là automat không đơn định đoán nhận ngôn ngữ L = {0m1n với m  1, n  0}.

Theo định lý trên, ta đi xây dựng M‟ = <Q‟, , ‟, q0‟, F‟> đơn định tương đương đoán nhận cùng một ngôn ngữ trên.

- Q‟ = {q0], [q1], [q2], [q0 , q1], [q0 , q2], [q1 , q2], [q0 , q1 , q2]}

- q0‟ = [q0] = A ;

- F‟ = {[q2], [q0, q2], [q1 , q2], [q0 , q1 , q2]}

- ‟:

‟([q0], 0) = (q0, 0) = [q0, q1]; (1)

‟([q0], 1) = (q0, 1) =  ;

‟([q1], 0) = (q1, 0) =  ;

‟([q1], 1) = (q1, 1) = [q2];		(2)
‟([q2], 0) = (q2, 0) =  ;
‟([q2], 1) = (q2, 1) = [q2];		(3)
‟([q0, q1], 0) = (q0, 0) (q1, 0) = [q0, q1];		(4)
‟([q0, q1], 1) = (q0, 1) (q1, 1) = [q2];		(5)
‟([q0, q2], 0) = (q0, 0) (q2, 0) = [q0, q1]	;	(6)
‟([q0, q2], 1) = (q0, 1) (q1, 1) = [q2] ;		(7)
‟([q1, q2], 0) = (q1, 0) (q2, 0) =  ;

‟([q1, q2], 1) = (q1, 1) (q2, 1) = [q2] ; (8)

‟([q0, q1, q2], 0) = (q0, 0) (q1, 0) (q2, 0) = [q0, q1]; (9)

‟([q0, q1, q2], 1) = (q0, 1) (q1, 1) (q2, 1) = [q2]; (10) Đặt [q0 ] = A;

[q0 , q1] = B;

[q1] = C;

[q2 ] = D;

[q0, q2] = E;

[q1, q2] = H;

[q0, q1 , q2] = I;

Từ: (1) ‟(A, 0) = B;

(2) ‟(C, 1) = D;

(3) ‟(D, 1) = D;

(4) ‟(B, 0) = B;

(5) ‟(B, 1) = D;

(6) ‟(E, 0) = B;

(7) ‟(E, 1) = D;

(8) ‟(H, 1) = D;

(9) ‟(I, 0) = B;

(10) ‟(I, 1) = D.

Sau khi loại đi các trạng thái thừa, ta có automat hữu hạn đơn định M‟ tương ứng với M. Trong đó:

- Q‟= {A, B, D} ;

- F‟ = {D};

- q‟0 = A;

- ‟: ‟(A, 0) = B ;

‟(B, 0) = B ;

‟(B, 1) = D ;

‟(D, 1) = D ;

Start

A

0

B

1

D

0

1

Hình 2.12. Automat hữn hạn đơn định đoán nhận ngôn ngữ L

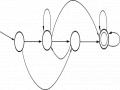
2.1.5. NFA với ε-dịch chuyển (NFAε)

Ta mở rộng mô hình NFA cho phép các phép chuyển trên nhãn rỗng ε. Automat hữu hạn không đơn định với ε - dịch chuyển được biểu diễn bằng đồ thị dưới đây đoán nhận các xâu gồm một số bất kỳ (không thể là 0) chữ số 0 sau đó là một số bất kỳ chữ số 1(có thể là 0) và cuối cùng là một số bất kỳ chữ số 2 (có thể là

0) . Thông thường, ta nói NFA đoán nhận một xâu w nếu có một dãy các phép

Xem tất cả 254 trang.