- Q = q0, q1, q2, q3;
- F = q0;
- :
(q0, 0) = q2 ; (q0, 1) = q1 ; (q1, 0) = q3 ; (q1, 1) = q0 ;
(q2, 0) = q0 ; (q2, 1) = q3 ; (q3, 0) = q1 ; (q3, 1) = q2
(Hàm chuyển thuộc dạng 1).
2) Cho automat hữu hạn M = <Q, , , q0, F> trong đó:
- Q = q0, q1, q2, q3;
- = 0,1;
- q0 = q0 ;
- F = q3;
- :
(q0, 0) = q2 ; (q0, 1) = q1 ;
(q1, 0) = q2 ; (q1, 1) = {q1, q3 } ;
(q2, 0) = q3 ; (q2, 1) = q1 ;
(q3, 0) = q3 ; (q3, 1) = q3.
(Hàm chuyển thuộc dạng 2).
2.1.1. Biểu diễn Automat hữu hạn
1) Phương pháp đồ thị
Để tiện cho việc xem xét một cách trực quan, người ta dùng sơ đồ để biểu diễn Automat, phương pháp này gọi là phương pháp đồ thị. Trong đồ thị, người ta biểu diễn mỗi Automat ứng với một đồ thị có hướng, có trọng số. Mỗi trạng thái của Q ứng với một đỉnh của đồ thị; mỗi cung có hướng đi từ đỉnh q đến đỉnh p có trọng số là a nếu (q, a) = p.
2) Phương pháp bảng
Trong phương pháp này, người ta dùng bảng gồm m dòng, n cột trong đó m là số trạng thái của Q, n là số kí tự vào của bảng chữ cái vào .
- Mỗi hàng là một trạng thái qi với i = 1, ..., m ;
- Mỗi cột là một ký hiệu vào aj với j = 1, ..., n;
- Ô (i, j), giao của hàng i và cột j là qk nếu (qi, aj) = qk.
Ví dụ 1: Cho automat M = <Q, , , q0, F> trong đó:
- q0 = q0 ;
- = 0, 1;
- Q = q0, q1, q2, q3;
- F = q0;
- :
(q0, 0) = q2 ; (q0, 1) = q1 ; (q1, 0) = q3 ; (q1, 1) = q0 ;
(q2, 0) = q0 ; (q2, 1) = q3 ; (q3, 0) = q1 ; (q3, 1) = q2
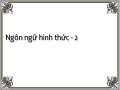
Biểu diễn của automat trên bằng phương pháp đồ thị
0
0
1
Start
q0
1
q1
q2
1
q3
1
0
0
Hình 2.2. Biểu diễn Automat bằng đồ thị
Biểu diễn automat bằng bảng
- q0 = q0 ;
- F = q0
0 | 1 | |
q0 | q2 | q1 |
q1 | q3 | q0 |
q2 | q0 | q3 |
q3 | q1 | q2 |
Có thể bạn quan tâm!
-
Ngôn ngữ hình thức - 2 -
Tính Chất 5 (Tính Đệ Quy Của Ngôn Ngữ) -
Văn Phạm Chính Quy Và Automat Hữu Hạn -
Automat Hữu Hạn Không Đơn Định-Nfa (Nondeterministic Finite Automata) -
Automat Hữn Hạn Đơn Định Đoán Nhận Ngôn Ngữ L -
Sự Tương Đương Giữa Nfa Có Và Không Có Ε-Dịch Chuyển
Xem toàn bộ 254 trang tài liệu này.
Bảng 2.1. Bảng chuyển trạng thái Ví dụ 2: Cho automat hữu hạn M = <Q, , , q0, F> trong đó:
- Q = q0, q1, q2, q3;
- = 0,1;
- q0 = q0 ;
- F = q3;
- :
(q0, 0) = q2 ; (q0, 1) = q1 ;
(q1, 0) = q2 ; (q1, 1) = {q1, q3 } ;
(q2, 0) = q3 ; (q2, 1) = q1 ;
(q3, 0) = q3 ; (q3, 1) = q3.
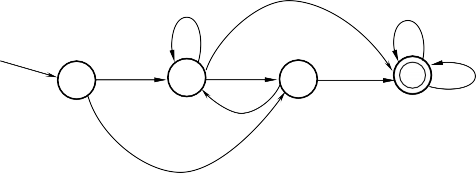
Biểu diễn của automat trên bằng phương pháp đồ thị
1
1 1
Start
q01
q10
1
q2 0 q30
0
Hình 2.3. Đồ thị biểu diễn Automat
Biểu diễn automat bằng bảng
- q0 = q0 ;
- F = q3;
0 | 1 | |
q0 | {q2} | {q1} |
q1 | {q2} | {q1,q3} |
q2 | {q3} | {q1} |
q3 | {q3} | {q3} |
Bảng 2.2. Bảng chuyển trạng thái
2.1.2. Automat hữu hạn đơn định
1) Định nghĩa
Cho Automat hữu hạn M = <Q, , , q0, F >, ta gọi M là Automat hữu hạn đơn định nếu:Với a, q Q ta có (q, a) = 1 và hàm chuyển có dạng 1 (*)
Cụ thể:
Automat hữu hạn đơn định là một hệ thống gồm 5 thành phần; ký hiệu là M =
<Q, , , q0, F>, trong đó:
Q - Tập hữu hạn khác rỗng các trạng thái.
- Tập hữu hạn khác rỗng các ký hiệu vào (gọi tắt là bảng chữ cái vào).
- Ánh xạ còn gọi là hàm chuyển trạng thái có dạng:
: Q Q (q, a) p
q0 - Là trạng thái bắt đầu; q0 Q.
F - Tập con của Q ( F Q) là tập các trạng thái kết thúc.
Nếu p là ảnh của (q, a) qua ánh xạ thì ký hiệu là (q, a) = p; với q, pQ; a và được gọi là một phép chuyển từ trạng thái q sang trạng thái p khi automat nhận ký tự vào là a.
Như vậy, Automat hữu hạn đơn định đang ở trạng thái q, nhận một ký tự vào a thì nó hoặc không thay đổi trạng thái (chuyển vào chính nó) hoặc xác định duy nhất một trạng thái chuyển tiếp theo.
Ngược lại, Automat không thoả mãn điều kiện (*) gọi là Automat không đơn định (Nondeterministic Automat). Nếu M là Automat hữu hạn không đơn định thì sẽ a, q Q sao cho (q, a) 1 hay (q, a) sẽ là một tập con của Q.
2) Hàm chuyển trạng thái mở rộng
Để có thể mô tả cách hình thức hoạt động của DFA trên một xâu vào, ta mở rộng hàm chuyển δ để áp dụng đối với một trạng thái trên một xâu. Ta định nghĩa hàm chuyển mở rộng δ* là một ánh xạ từ Q × Σ* → Q với ý nghĩa δ*(q, w) là trạng thái DFA chuyển đến từ trạng thái q trên xâu vào w:
1. δ* (q, ε) = q
2. δ*(q, wa) = δ(δ*(q, w), a); với q Q; w Σ* và a Σ.
Suy ra:
*(q, a a ... a ) = q, a1 an-1an
1 2 n
*(q, a a ... a ) = q, a1 an-1an
1 2 n
= q1, a2 an-1an
= …
= q n-2, an-1an
= qn-1, an
= qn
Ví dụ: Cho Automat hữu hạn M = <Q, , , q0 , F>
Q = q0, q1, q2, q3; = 0, 1; q0 = q0 ; F = q0
Hàm chuyển xác định như sau:
(q0, 0) = q2; (q0, 1) = q1; (q1, 0) = q3; (q1, 1) = q0; (q2, 0) = q0;
(q2, 1) = q3; (q3, 0) = q1; (q3, 1) = q2.
Hãy tính (q2, 1010).
Áp dụng công thức (1), ta có:
(q2, 1) = q3; (q3, 0) = q1; (q1, 1) = q0; (q0, 0) = q2;
Vậy (q2, 1010) = q2.
3) Ngôn ngữ đoán nhận bởi automat hữu hạn đơn định
Cho Automat hữu hạn đơn định M = <Q, , , q0, F>, ta gọi ngôn ngữ đoán nhận bởi Automat hữu hạn đơn định M là tập:
L(M) = w Σ* *(q0,w) = qF và w*
Như vậy, ngôn ngữ đoán nhận bởi Automat hữu hạn đơn định DFA M là tập tất cả các xâu vào w* sao cho khi Automat ở trạng thái ban đầu q0, nhận từ vào w thì nó có thể chuyển dịch về trạng thái kết thúc thuộc tập F.
Một xâu vào w = a a
1 2
... a
n
được đoán nhận bởi một DFA nếu có tồn tại một dãy
các phép chuyển, tương ứng với xâu vào, từ trạng thái bắt đầu đến trạng thái kết thúc.
w = a1 a2 a3 … an -1 an
q0 q1 q2 ... qn-1 qn
Hình 2.4. Mô tả quá trình DFA M đoán nhận xâu
Như vậy, để kiểm tra một xâu vào w = a1 a2 ... an được đoán nhận bởi một NFA hay không ?. Ta phải tính *(q0,w).
*(q0,w) = *(q0, a a ... a ) = q0, a1 an-1an
1 2 n
= q0, a1 an-1an
= q1, a2 an-1an
= …
= q n-2, an-1an
= qn-1, an
= qn
Nếu qn F thì w N(M); ngược lại qn F thì w N(M). Ở đây q1 q2 qn Q.
Ví dụ:
Cho Automat hữu hạn M = <Q, , , q0 , F> trong ví dụ trên và được biểu diễn dưới dạng bảng là:
q0 = q0 ; F = q0
0 | 1 | |
q 0 | q 2 | q 1 |
q 1 | q 3 | q 0 |
q 2 | q 0 | q 3 |
q 3 | q 1 | q 2 |
Bảng 2.3. Biểu diễn automat bằng bảng
Hãy kiểm tra xem xâu w = 110101 có thuộc L(M) không?. Ta có δ(q , 1) = q ;
0 1
δ(q , 1) = q ;
1 0
δ(q0, 0) = q2;
(q2, 1) = q3;
(q3, 0) = q1;
(q1, 1) = q0;
Và cuối cùng δ*(q , 110101) = q F. Vậy 110101 L(M).
0 0
Ta có thể chứng minh được rằng L(M) là tập mọi xâu có số chẵn số 0 và số chẵn số 1.
Từ các kết quả trên, ta có giải thuật sử dụng DFA để đoán nhận xâu của ngôn ngữ.
4) Giải thuật mô phỏng hoạt động của một DFA
Input : Xâu vào w kết thúc bởi $
Output: Câu trả lời "YES" nếu DFA đoán nhận được xâu w
và "NO" nếu ngược lại.
Process
Ví dụ:
q := q ;
0
c := getchar() ; {c là ký hiệu vào đầu tiên}
While c < > $ do begin
q := δ(q, c);
c := nextchar(); {c là ký hiệu vào được đọc tiếp theo} end;
If q F then write("YES" )
Else write("NO" )
Sử dụng giải thuật trên với automat được cho ở hình 2.5
để đoán nhận các từ sau:
- w = bbaaabb$
a
Start
0
a
1
b
2
b
3
b
Hình 2.5. Đồ thị biểu diễn Automat
Ta trình bày giải thuật sử dụng automat đơn định đoán nhận w bằng bảng sau: