Hiệu Chỉnh Kết Quả Đo Và Đánh Giá Sai Số Kết Qủa Phân Tích

2.5. Hiệu chỉnh kết quả đo và đánh giá sai số kết qủa phân tích

2.5.1. Đánh giá sai số

2.5.1.1. Sai số ngẫu nhiên

Sai số ngẫu nhiên là những sai số và đặc điểm của nó đến mỗi kết quả đo đạc không rõ ràng, khi thì xuất hiện thế này, lúc thì xuất hiện thế kia, ta không thể biết trước được trị số và dấu của nó. Vì vậy, sai số ngẫu nhiên xuất hiện ngoài ý muốn chủ quan của con người, chủ yếu do điều kiện bên ngoài, ta khó khắc phục mà chỉ có thể tìm cách hạn chế ảnh hưởng của nó.

Sai số ngẫu nhiên có các đặc tính sau: sai số ngẫu nhiên có trị số và dấu xuất hiện không theo quy luật, nhưng trong cùng một điều kiện đo nhất định, sai số ngẫu nhiên sẽ xuất hiện theo những quy luật. Bất kỳ đại lượng ngẫu nhiên nào (kết quả đo) được đặc trưng bởi hàm phân bố nào xác định xác suất xuất hiện các quá trình khác nhau của nó trong quá trình đó.

Thông thường người ta cho rằng, các kết quả thực nghiệm có chứa các sai số ngẫu nhiên, tuân theo quy luật phân phối chuẩn hay phân phối Gauss hàm mật độ phân bố xác suất là phân phối chuẩn có dạng:

𝑓(𝑥) =1 𝑒

√2𝜋𝜎

−(𝑥−𝜇)2

2𝜎2 (2.34)

Công thức trên cho thấy hàm mật độ được đặc trưng bởi hai tham số:

- Giá trị trung bình của đại lượng đo µ và độ lệch quân phương  xác định độ phân tán của các kết quả đo xung quanh giá trị trung bình.

µ = 𝑋̅ = 𝑥1+𝑥2+𝑥3+⋯𝑥𝑛

𝑛

𝜎 = √(𝑥𝑖−𝑋̅)2

𝑛−1

Trong đó: xi - kết quả đo thứ i; n - tổng số phép đo.

(2.35)

(2.36)

Số lượng hạn chế của tài liệu thực nghiệm không cho phép xác định chính xác giá trị thực của µ và , chính vì thế người ta đưa ra khoảng tin cậy trong phạm vi khoảng đó với xác suất xác định, xác suất tin cậy, tìm được giá trị thực của các đại lượng đã nêu µ và .

2.5.1.2 Sai số của các đại lượng đo

Nếu như đại lượng đo được x là hàm của n đại lượng độc lập ngẫu nhiên x1, x2…xn tức là z = f(x1, x2…xn ) thì sai số bình phương trung bình xác định z được tìm theo công thức sau:

𝛿(%) = √( 𝜕𝑧 )2𝛿2 + ( 𝜕𝑧 )2𝛿2 + ⋯ + ( 𝜕𝑧 )2𝛿2 (2.37)

𝜕𝑥1

𝑥1

𝜕𝑥2

𝑥2

𝜕𝑥𝑛

𝑥𝑛

Trong trường hợp: z = x1 = x2 = … = xn

Thì ( 𝜕𝑧 )2 = 1 và 𝜎

= √𝜕2 + 𝜕2 + ⋯ + 𝜕2 (2.38)

𝜕𝑥2

2.5.1.3. Đánh giá kết quả đo

𝑧 𝑥1

𝑥2

𝑥𝑛

Việc đánh giá các phép đo phóng xạ dạng xung có thể tiến hành bằng 2 phương pháp:

- Dựa trên các tính chất của luật Poatson

- Phương pháp thông thường dựa trên các phép đo lặp của cùng một đại lượng

Phương pháp thứ nhất có thể được dùng trong các trường hợp khi xác định rằng, máy làm việc không có nhiễu, nghĩa là đã biết được quy luật phân phối lý thuyết. Phương pháp không đòi hỏi các phép tính phức tạp và cho cách đánh giá tin cậy của sai số gây ra do các thăng giáng thống kê của tốc độ đếm. Phương pháp này có thể được dùng cả khi tiến hành một phép đo. Độ tin cậy của các đánh giá nhận được không phụ thuộc vào số lượng các phép đo mà được xác định bởi số lượng tổng cộng các xung ghi được, nó tăng tỷ lệ với căn bậc hai của số xung ghi được.

Phương pháp thứ hai có thể dùng được khi máy làm việc không ổn định, bởi vì sai số được tính trên độ phân tán các số liệu thực nghiệm, việc đánh giá các kết quả đo sẽ đáng tin cậy, nếu như phép đo không nhỏ hơn 20. Khi số các phép đo chừng 3 đến 5, việc đánh giá chỉ xem là áng chừng. Phương pháp đòi hỏi việc tính toán khá phức tạp. Tuy nhiên nó có ưu điểm là có thể dùng không chỉ với các phép đo xung mà bất kỳ dạng khác nào của phép đo và có thể tự động hóa tính các sai số. Chính vì thế trên thực tế phương pháp thứ nhất thường được dùng chỉ thiết lập các phép đo (chọn các điều kiện tối ưu của phép đo, độ nhạy máy, trọng lượng mẫu…). Còn phương pháp thứ hai được dùng khi xử lý số liệu thực nghiệm.

Khi xử lý các kết quả đo, người ta tính độ chính xác của các đại lượng đo trực tiếp cũng như các đại lượng được tính theo các giâ trị đo được. Các công thức để xác định độ chính xác của các đại lượng đo được đưa vào Bảng 2.9.

Bởi vì các giá trị sai số ngẫu nhiên phụ thuộc vào hàm lượng của nguyên tố được xác định và vào lượng tương đối của các nguyên tố nhiễu. Bởi vậy, khi đánh giá mức độ sai số ngẫu nhiên cần thiết chia các mẫu thành các nhóm theo các khoảng hàm lượng của các nguyên tố phân tích và theo các khoảng hàm lượng tương đối của các nguyên tố nhiễu. Độ lớn khoảng hàm lượng trong các nhóm được chọn sao cho các số nhóm không nhỏ hơn 5.

Bảng 2.9. Các công thức để xác định độ chính xác của các phép đo phóng xạ

Đại lượng được xác định

Phương pháp dựa trên phân phối Poatson	Phương pháp dựa trên đo lặp
Tốc độ đếm trung bình	∑ 𝑁𝑖 𝑛̅ = ∑ 𝑡 𝑖 Trong đó Ni số xung ghi được trong thời gian ti. trong trường hợp riêng t1=t2=…=ti=t’	∑ 𝑁𝑖 𝑛̅ = ∑ 𝑡′ 𝑚 Với t’ thời gian của một phép đo; m là số phép đo
Sai số bình phương trung bình trong việc xác định tốc độ đếm trung bình	Nếu như lấy một phép đo thì: ∑ 𝑁𝑖 = 𝑁; ∑ 𝑡𝑖 =𝑡′ 𝜎 = √ 𝑛̅ = √𝑛̅ = √𝑁 ∑ 𝑡𝑖 𝑡′ 𝑡	∑(𝑛𝑖− 𝑛̅)2 𝜎 = √ 𝑛(𝑚 − 𝑖) Trong đó ni = Ni/t’
Sai số tương đối	𝜎 𝛿 = 𝑛 . 100%	𝜎 ℇ = 𝑛 . 100%

Có thể bạn quan tâm!

• Một Số Mẫu Đất Đá Được Nhốt Chờ Đo Phổ.
• Ngưỡng Phát Hiện Của Hệ Phổ Kế Gamma Dùng Detector Bán
• Quy Trình Đánh Giá Ảnh Hưởng Của Phóng Xạ Môi Trường Trong Hoạt Động Khoáng Sản Chứa Norm
• Đặc Điểm Phân Bố Nồng Độ Khí Phóng Xạ Radon
• Đánh Giá Suất Liều Bức Xạ Gamma Và Nồng Độ Khí Radon
• Tương Quan Giữa Các Hạt Nhân Phóng Xạ Khác Nhau Trong

Xem toàn bộ 162 trang tài liệu này.

2.5.2. Hiệu chỉnh sự sai khác giữa khối lượng mẫu chuẩn và mẫu phân tích Về nguyên tắc có nhiều nguyên nhân gây ra sai số: Sai số do sự chồng chập xung, sai số do sự không đồng nhất giữa mẫu chuẩn và mẫu phân tích về

hình học đo, thành phần chất nền. Tuy nhiên với mẫu môi trường thì hoạt độ

phóng xạ nhỏ ngay cả khi mẫu đặt ngay sát bề mặt detector, thời gian chết của thiết bị không quá 1%. Vì vậy sai số do sự chồng chập xung gây ra mất số đếm tại đỉnh hấp thụ toàn phần hoàn toàn có thể bỏ qua [52, 77].

Khi xác định hoạt độ phóng xạ riêng theo phương pháp phổ gamma, dựa theo phương pháp tương đối hay dựa vào đường cong hiệu suất ghi tuyệt đối tại đỉnh hấp thụ toàn phần nếu có sự sai khác về hình học đo, khối lượng, thành

phần mẫu chuẩn và mẫu phân tích sẽ gây ra sai số. Trong Luận án này tất cả các mẫu phân tích đều được đựng trong cùng 1 loại hộp đồng nhất, thể tích mẫu như nhau, mẫu chuẩn và mẫu phân tích đều được đặt trực tiếp sát detector vì vậy sự sai lệch về hình học đo giữa mẫu chuẩn và mẫu phân tích có thể bỏ qua. Sự sai lệch về thành phần chất nền và khối lượng giữa mẫu chuẩn và mẫu phân tích sẽ dẫn tới sự sai khác hệ số tự hấp thụ các bức xạ gamma trong mẫu chuẩn và mẫu phân tích. Sự sai lệch về sự tự hấp thụ trong mẫu chuẩn và mẫu phân tích càng lớn khi năng lượng bức xạ gamma đặc trưng được chọn phân tích càng nhỏ [77]. Ngoài ra, để hiệu chỉnh sự sai khác thành phần chất nền giữa mẫu phân tích và mẫu chuẩn, cần phải tiến hành thực nghiệm đo hệ số suy giảm khối μ của bức xạ gamma được chọn để tính hoạt độ phóng xạ trong mỗi mẫu phân tích cụ thể, sau đó thay vào công thức hiệu chỉnh. Luận án đã sử dụng phương pháp đường cong chuẩn nội hiệu suất ghi kết hợp hiệu suất ghi tuyệt đối tại đỉnh 1460,8 keV của 40K cho phép khắc phục sự sai khác giữa thành phần chất nền

giữa mẫu chuẩn và mẫu phân tích.

2.5.3. Công thức truyền sai số

Trong Luận án, các đại lượng cần tìm đều được xác định thông qua nhiều đại lượng. Để tính độ lệch chuẩn của một hàm số theo độ lệch chuẩn của đối số, ta dựa vào công thức truyền sai số.

Xét trường hợp tổng quát, giả sử co một hàm số f(x1,x2...xn) phụ thuộc vào n đại lượng x1, x2…xn, thông thường các đại lượng này có thể xác định được bằng thực nghiệm mà từ đó ta có thể tính được giá trị của hàm f(xi) tương ứng. Các biến xi có các giá trị trung bình tương ứng là 𝑥̅𝑖với sai số chuẩn i. Cũng như cách chúng ta cần xác định sai số chuẩn của f(x1,x2...xn).

Giả thiết rằng f(x1,x2...xn) có thể khai triển thành chuỗi Taylor xung quanh các giá trị trung bình 𝑥̅𝑖.

𝑓(𝑥 ) = 𝑓(𝑥̅) + ∑𝑛

(𝑥

− 𝑥̅) 𝜕𝑓

+ 𝑂(𝑥

− 𝑥̅)2(2.39)

𝑖 𝑖

𝑖=1 𝑖

𝑖 𝜕𝑥̅𝑖

𝑖 𝑖

trong đó: 𝜕𝑓

= 𝜕𝑓 (𝑥 = 𝑥̅)

𝜕𝑥̅𝑖

𝜕𝑥𝑖 𝑖 𝑖

Thừa số 𝑂(𝑥𝑖− 𝑥̅𝑖)2bao gồm tất cả thừa số tương ứng với vi phân bậc hai trở lên, ở một giới hạn chính xác nào đó, các thừa số này có thể bỏ qua, khi đó hàm f(x) có thể được viết gọn lại như sau:

𝑓(𝑥 ) = 𝑓(𝑥̅) + ∑𝑛

(𝑥

− 𝑥̅) 𝜕𝑓

(2.40)

𝑖 𝑖

𝑖=1 𝑖

𝑖 𝜕𝑥̅𝑖

Như vậy, giá trị trung bình f(xi) là giá trị được coi là gần với giá trị thực cần xác định.

𝑓̅ = 𝑓(𝑥̅𝑖)

Trong hầu hết các trường hợp, các hệ số tương quan giữa các biến xi bằng không. Vì vậy, sai số chuẩn của f(xi) được tính theo công thức sau [53, 99]:

𝜎 = √∑𝑛 ( 𝜕𝑓

2

𝜎2

𝑓 𝑖

)

𝜕𝑥𝑖

𝑖

, (2.41)

trong đó: - σf là độ lệch chuẩn của đại lượng f,

- σi là độ lệch chuẩn của đại lượng xi,

2.5.4. Các nguồn gây ra sai số

2.5.4.1. Trong bài toán xác định hoạt độ phóng xạ theo phổ kế gamma bán dẫn khi xác định hoạt độ phóng xạ riêng có các nguồn sai số sau:

- Độ lệch chuẩn do xác định tốc độ đếm < 4%;

- Sai số do xác định hiệu suất ghi tuyệt đối tại đỉnh hấp thụ toàn phần

< 1,5%;

- Sai số hệ số phân nhánh < 1,5%;

- Sai số từ việc cân xác định khối lượng < 0,1%;

Sai số được lấy bằng 2 lần độ lệch chuẩn (±2σ), kết quả sai số tương đối

< 9%.

2.5.4.2. Trong phương pháp xác định hoạt độ phóng xạ theo phương pháp ma trận, các nguồn sai số chính như sau:

- Sai số do việc xác định các hệ số ảnh hưởng < 3%;

- Sai số thống kê từ tốc độ đếm tại các đỉnh năng lượng < 2%;

- Sai số khi xác định phương trình phân tích xác định hàm lượng riêng theo tốc độ đếm tại các kênh < 3,5%;

- Thăng giáng do sự trôi kênh gây ra < 2%.

CHƯƠNG 3. KẾT QUẢ VÀ THẢO LUẬN

3.1. Mô hình địa môi trường nghiên cứu cơ chế phát tán phóng xạ tới môi trường

Có 3 loại mô hình thường được sử dụng để nhận thức đối tượng nghiên cứu trong lĩnh vực khoa học trái đất nói chung, địa chất môi trường nói riêng, cũng như mô tả định lượng sự biến đổi các tính chất địa chất, địa chất môi trường, đó là:

- Mô hình địa hóa môi trường: được thể hiện dưới dạng biểu đồ, sơ đồ hoặc mặt cắt; trên đó thể hiện các yếu tố địa chất - khoáng sản và các yếu tố môi trường liên quan;

- Mô hình “hình học mỏ”: sử dụng để thành lập các sơ đồ, bản đồ phân bố hàm lượng các nhân phóng xạ và các kim loại nặng cho từng vùng, từng khu vực nghiên cứu; là cơ sở khoanh định các khu vực ô nhiễm, khu vực có khả năng ô nhiễm và khu vực an toàn về phóng xạ và kim loại nặng trong môi trường nước, đất.

- Mô hình toán học: sử dụng toán xác suất thống kê, hàm ngẫu nhiên, các mô hình lan truyền, phương pháp Kriging…

Trong Luận án, tác giả đưa ra sơ đồ cấu trúc kết hợp các mô hình để giải quyết nhiệm vụ nghiên cứu của mình như sau (Hình 3.1).

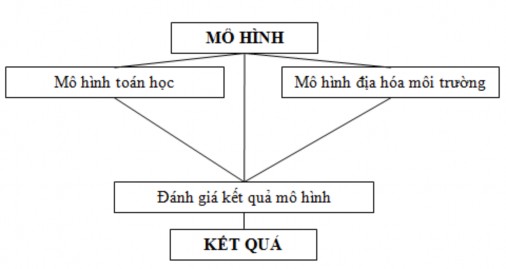
Hình 3.1. Sơ đồ kết hợp các mô hình để đánh giá hiện trạng phóng xạ môi trường do tác giả phát triển

Để áp dụng mô hình hóa đối tượng nghiên cứu bằng mô hình địa môi trường cần thu thập, tổng hợp tài liệu địa chất khoáng sản và tài liệu phóng xạ

môi trường. Công tác thu thập tài liệu được tiến hành trên tất cả các tài liệu liên quan đến mỏ, điểm khoáng sản phóng xạ, mỏ khoáng sản chứa phóng xạ ở các khu mỏ nghiên cứu gồm [34]:

- Tài liệu địa chất: đặc điểm địa chất khu mỏ, đặc điểm đá chứa quặng, đá vây quanh; diện phân bố quặng trong không; các kết quả địa hóa (chủ yếu là vành phân tán địa hoá thứ sinh, nguyên sinh của các nhân phóng xạ); kết quả phân tích mẫu khoáng sản có chứa các nhân phóng xạ tự nhiên.

- Tài liệu địa vật lý: gồm vành đồng lượng suất liều gamma trên khu vực nghiên cứu; các dị thường, qui mô các dị thường, so sánh chúng với số liệu đo tại thân quặng, đới quặng; bậc dị thường phóng xạ và quan hệ của chúng với bậc nồng độ hoạt độ phóng xạ; kết quả phân tích các tham số vật lý…

- Tài liệu địa chất thuỷ văn - địa chất công trình gồm: đặc điểm địa chất thủy văn tầng chứa nước, mực nước thuỷ tĩnh, vị trí các điểm xuất lộ nước ngầm...; đặc điểm địa chất thuỷ văn, hệ thống sông suối, lưu lượng nước...; đặc điểm địa chất công trình của các loại đất đá, lớp đá chứa quặng, đá vây quanh quặng; các hiện tượng trượt lở đất, đá đổ...; kết quả phân tích mẫu nước.

- Các loại tài liệu khác gồm các báo cáo kết quả đánh giá tác động môi trường đã và đang thực hiện liên quan đến khu mỏ (nếu có); tài liệu về tai biến địa chất và môi trường; hệ thống cơ sở dữ liệu địa chất - khoáng sản và cơ sở dữ liệu môi trường; các tài liệu liên quan đến tiêu chuẩn môi trường, các văn bản pháp luật của nhà nước và quốc tế về môi trường.

Như vậy, mô hình địa môi trường là “một tổ hợp thông tin về địa chất, địa hóa, địa vật lý, thủy văn, kỹ thuật - công nghệ liên quan với hành vi địa hóa của các mỏ khoáng sản tương tự nhau về mặt địa chất có trước, trong và sau khi có các hoạt động thăm dò, khai thác và chế biến khoáng sản” [34].

Mô hình địa môi trường cho ta thông tin về biến đổi địa hóa tự nhiên liên quan với kiểu mỏ, các biến đổi địa hóa liên quan với quá trình hoạt động khoáng sản, các chất thải, các quá trình chế biến khoáng sản. Các dữ liệu bao gồm về cả chất rắn, nước và không khí. Từ các dấu hiệu trên, tác giả đưa ra sơ đồ cấu trúc mô hình địa môi trường như Hình 3.2.

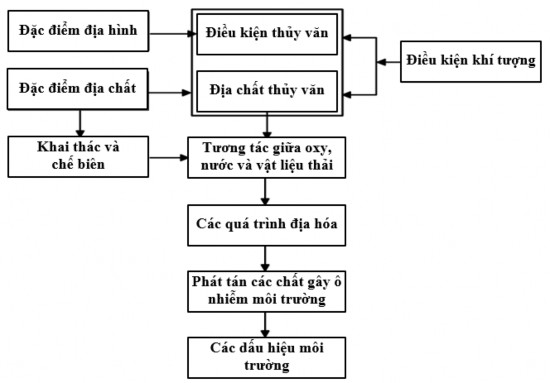
Hình 3.2. Sơ đồ cấu trúc mô hình địa môi trường.

Trong nội dung của luận án, tác giả đã nghiên cứu cơ chế phát tán phóng xạ ra môi trường và đánh giá mức liều bức xạ tự nhiên cho người dân sinh sống tại khu vực mỏ khoáng sản đất hiếm (Mường Hum) và mỏ sa khoáng monazite (Bản Gié).

Phân tích tổng hợp tài liệu tại các khu mỏ, tác giả đã xác định được mức liều bức xạ tại các mỏ sa khoáng và đất hiếm.

3.2. Đánh giá ảnh hưởng của phóng xạ môi trường tại mỏ đất hiếm Mường Hum

3.2.1. Đánh giá sự phát tán các nhân phóng xạ ra môi trường

3.2.1.1. Đặc điểm môi trường nước

Nước trong vùng có độ pH dao động trong khoảng 6,8÷7,6, trung bình 7,1 đặc trưng cho môi trường trung tính. Thế oxy hóa khử Eh dao động trong khoảng (123÷145) mV, trung bình 126,2 mV, đặc trưng thế oxy hóa yếu (100 mV < Eh < 150 mV).

Như vậy, nước trong khu vực mỏ Mường Hum đặc trưng môi trường trung tính - oxy hóa yếu (6,5 < pH < 7,5; 100 mV < Eh < 150 mV) phân bố trong toàn khu vực. Đây là môi trường thuận lợi cho sự hòa tan các hợp chất urani

Xem tất cả 162 trang.