26 Chương 1 Cơ sđ lý thuyát mụ tÊ tỏn xÔ hÔt nhõn-hÔt nhõn
1.3 Hằ phương trỡnh liờn kờnh cho tỏn xÔ phi đàn hỗi
Khi xột đán tỏn xÔ phi đàn hỗi, đº đơn giÊn, ta xột khụng gian cơa toỏn tỷ P gỗm hai kờnh, kờnh tỏn xÔ đàn hỗi (β) và kờnh phi đàn hỗi (γ)
P Ψ = χβ (R)ψβ + χγ (R)ψγ . (1.43)
Trong trướng hủp này, đº đơn giÊn ta xột hÔt nhõn bia đưủc kớch thớch lờn trÔng thỏi cú spin Iγ . Vỡ kờnh phi đàn hỗi ch¿ làm thay đời trÔng thỏi năng lưủng cơa cỏc nucleon trong hÔt nhõn bưn tợi và hÔt nhõn bia so vợi kờnh đàn hỗi, do đú ta cú Vβ = Vγ = V , Rβ = Rγ = R. Bờn cÔnh đú, hàm súng cơa cỏc trÔng thỏi nucleon thọa món tớnh chĐt trỹc giao chuân húa, dăn đán hàm súng nởi cơa 2 kờnh này cũng thọa món
hψβ |ψγ i = δβγ . (1.44)
Có thể bạn quan tâm!
-
Nghiên cứu hiệu ứng cầu vồng và cơ chế chuyển alpha trong tán xạ ở năng lượng thấp và trung bình - 3 -
Cơ Sđ Lý Thuyát Mụ Tê Tỏn Xô Hôt Nhõn-Hôt Nhõn -
Cơ Sđ Lý Thuyát Mụ Tê Tỏn Xô Hôt Nhõn-Hôt Nhõn -
Cơ Sđ Lý Thuyát Mụ Tê Tỏn Xô Hôt Nhõn-Hôt Nhõn -
Chương 2 Nghiờn Cựu Hiằu Ựng Cưu Vỗng Hôt Nhõn Trong Tỏn Xô Hôt 12C−12C Và 16O−12C -
Nghiờn Cựu Hiằu Ựng Cưu Vỗng Hôt Nhõn Trong Tỏn Xô Hôt 12C−12C Và 16O−12C
Xem toàn bộ 152 trang tài liệu này.
Tứ đú hằ phương trỡnh liờn kờnh CC đ (1.16) đưủc rỳt gồn vã dượi dÔng
Eβ − Kβ − Uβ (R) χβ (R) = Uβγ (R)χγ (R) (1.45a)
Eγ − Kγ − Uγ (R)χγ (R) = Uγβ (R)χβ (R), (1.45b)
vỵi Uβγ= Uγβ= hψβ |V |ψγ i là thá ngoài đướng chộo hay cũn đưủc gồi là thá dàch chuyºn, thá này đ°c trưng cho cướng đở dàch chuyºn tứ kờnh đàn hỗi lờn kờnh kớch thớch và ngưủc lÔi. Như đó đã cêp đ phƯn tỏn xÔ đàn hỗi, đõy là phương trỡnh cho bián tồa đở khụng gian 3 chiãu, ta cú thº chuyºn vã 1 chiãu thụng qua phương phỏp khai triºn súng riờng phƯn theo cỏc giỏ trà mụ men gúc quÿ đÔo L. Khỏc vợi tỏn xÔ đàn hỗi, hÔt nhõn bưn tợi và hat nhõn bia cú spin Iβ = 0 và mụ men gúc tờng bơng đỳng mụ men gúc quÿ đÔo Jβ = Lβ . Do kờnh phi đàn hỗi cú spin Iγ cú thº khỏc khụng, mụ men gúc quÿ đÔo Lγ kát c°p vợi spin Iγthành mô men góc têng Jγ = Lγ + Iγ. Ta cú đành luêt bÊo toàn mụ men gúc toàn phƯn
Jβ = Jγ = J ⇔ Lβ = Lγ + Iγ , (1.46)
26
Chương 1 Cơ sđ lý thuyát mụ tÊ tỏn xÔ hÔt nhõn-hÔt nhõn
khi đú hàm súng kờnh đàn hỗi và phi đàn hỗi đưủc viát dượi dÔng khai triºn súng riờng phƯn như sau [41]
X
√
χβ (R)ψβ
4π
β
(x) = (2Lβ
L
kβ R
4πX
β
+ 1)1/2χL
(R)ΦLβ0(Rˆ, x) (1.47a)
L 0
β
χγ (R)ψγ
(x)=
√
(2Lβ
L
kβ R
β
+ 1)1/2 χ
X
Lγ
Lβ Lγ
(R)ΦLβ0(Rˆ, x). (1.47b)
L I
γ γ
LI
Trong đú, chỳng ta sỷ dửng kớ hiằu ΦJ MJ
đº đành nghĩa hàm spin-gúc mụ tÊ
vecto kát c°p giỳa hàm Harmonic cƯu và hàm súng nởi hÔt nhõn như sau
LI
I
ΦJ MJ(Rˆ, x) = XiLhLM, IMI|JMJiYLM(Rˆ)ψMI(x)
M MI
hay đưủc viát gồn lÔi |LIJi =YL ⊗ ψI (x)J (1.48)
I
vỵi M là giỏ trà hỡnh chiáu cơa mụ men tương ựng, hLM, IMI |JMJ i là hằ số Clebsch-Gordan, và YLM = iLYLM , dĐu ⊗ ch¿ kát c°p giỳa hàm Harmonic cƯu YLM và hàm súng nởi ψMI (x) cơa hằ. Khi đú hằ phương trỡnh liờn kờnh
(1.45) trđ thành [41]
~2
X
2µβ
d2
dR2 + kβ −
Lβ (Lβ + 1)
!
R2
− hLβ0Lβ|V |Lβ0Lβi
χLβ (R)
= hLβ 0Lβ |V |Lγ Iγ Lβ iχLβ Lγ (R) (1.49a)
!
Lγ
~2
2µγ
d2
dR2 + kγ −
Lγ (Lγ + 1)
X
R2
− hLγIγLβ|V |LγIγLβi
χLβ Lγ (R)
=hLγ Iγ Lβ |V |Lβ 0Lβ iχLβ (R)+
L0γ 6=Lγ
hLγIγLβ|V |L0γIγLβiχLβL0γ(R). (1.49b)
Các giá trà Lγ đ hằ phương trỡnh trờn tuõn theo biºu thực cởng mụ men gúc (1.46), vỡ vêy Lβ − Iγ≤ Lγ≤ Lβ + Iγ . Cũng cƯn lưu ý rơng, khi ỏp
dửng phương phỏp khai triºn súng riờng phƯn, cỏc yáu tố ma trên tương
27
28 Chương 1 Cơ sđ lý thuyát mụ tÊ tỏn xÔ hÔt nhõn-hÔt nhõn
tác Uij = hψi|V |ψj i đ phương trình (1.45) đưủc đưa vã dượi dÔng xuĐt hiằn trong phương trỡnh (1.49)
LiIi
LjIj
hLiIiJ|V |LjIjJi = Z ΦJ MJ(Rˆ, x)∗V ΦJ MJ(Rˆ, x)dRˆdx. (1.50)
vỵi i và j =β ho°c γ. Chi tiát tớnh toỏn cỏc yáu tố ma trên này dỹa trờn mău folding kộp s³ đưủc trỡnh bày đ mửc 1.4.
Biờn đở tỏn xÔ phi đàn hỗi
β
Đº xỏc đành biờn đở tỏn xÔ phi đàn hỗi ta phÊi tián hành giÊi hằ phương trỡnh (1.49), thụng thướng hằ phương trỡnh này đưủc giÊi bơng phương phỏp l°p. Trược tiờn, vá phÊi phương trỡnh (1.49a) đưủc cho bơng 0, tứ đú ta cú thº tỡm đưủc hàm súng χLβ (R) bơng phương phỏp Numerov [44]. Sau đó, χLβ (R) đưủc thá vào phương trỡnh (1.49b) đº xác đành các hàm sóng χLβ Lγ (R). Bược tiáp theo ta lÔi thá ngưủc χLβ Lγ (R) vào (1.49a) đº tìm χLβ (R)..., cỏc bược đưủc l°p lÔi đán khi cỏc hàm súng hởi tử. Tứ đú ta cú thº xỏc đành cỏc dÔng tiằm cên cơa cỏc hàm súng riờng phƯn này. Trong đú, dÔng tiằm cên cơa hàm súng đ kờnh tỏn xÔ đàn hỗi theo tớnh toỏn CC cũng tương tỹ như đ tớnh toỏn đơn kờnh theo mău OM. Do đú, ta cũng thu đưủc biºu thực biờn đở tỏn xÔ đàn hỗi như đ biºu thực (1.42) như sau
fβ(θ) = fC
1
X
(θ) + (2Lβ
L
2ikβ
β
+ 1)e2iσLβSL
− 1PLβ
(cos θ). (1.51)
L
Đối vợi tỏn xÔ phi đàn hỗi, hàm súng ch¿ bao gỗm thành phƯn súng tỏn xÔ vợi dÔng tiằm cên đưủc xỏc đành [41]
χLβ Lγ
iLβ +1
→ − 2
(−1) β e
iσLβ
+σL0γ
SLβ Lγ
ei(
kγ R
−ηγ
ln 2kγ
R), (1.52)
vỵi SLβ Lγ
= e2iδLβLγlà ma trên tỏn xÔ ựng vợi kờnh phi đàn hỗi, σ0
và δLβ Lγ
Lγ
lƯn lưủt là đở lằch pha gõy ra bđi lỹc Coulomb và lỹc hÔt nhõn đ kờnh phi đàn hỗi. Thá phương trỡnh (1.52) vào phương trình (1.47b), ta thu đưủc dÔng
28
Chương 1 Cơ sđ lý thuyát mụ tÊ tỏn xÔ hÔt nhõn-hÔt nhõn
tiằm cên cơa χγ (R) như sau
χγ (R) →
ei(kγ R−ηγ ln 2kγ R)
fMγ (θ, φ) (1.53)
R
vỵi fMγ (θ, φ) là biờn đở tỏn xÔ phi đàn hỗi ựng vợi giỏ trà hỡnh chiáu Mγ cơa spin kích thích Iγ và đưđc xác đành [41]
X
√
fMγ
(θ, φ) =
4π
2ikβ
(2Lβ
Lβ Lγ
+ 1)1/2hLγ
− Mγ
, Iγ
Mγ |Lβ 0i
× e S
iσLβ+σL0γ
Lβ Lγ
YLγ −Mγ
(θ, φ) (1.54)
2
Tứ đõy, ta cú tiát diằn vi phõn theo gúc cho tỏn xÔ đàn hỗi và phi đàn hỗi
dσel. dΩ
= |fβ
(θ)| (1.55)
dσine. dΩ
= |fMγ
X
Mγ
(θ, φ)| (1.56)
2
1.4 Mău folding kộp cho thá tỏn xÔ hÔt nhõn-hÔt nhõn
Đ cỏc mửc trờn, Nghiờn cựu sinh (NCS) đó trỡnh bày cơ sđ lý thuyát mụ tÊ cỏc quỏ trỡnh điºn hỡnh gỗm tỏn xÔ đàn hỗi, phi đàn hỗi. Đº tỡm tiát diằn cơa cỏc quỏ trỡnh này chỳng ta phÊi giÊi cỏc phương trỡnh (1.24) ho°c (1.49) vợi thụng tin cƯn cung cĐp cho cỏc phương trỡnh này là cỏc yáu tố ma trên tương tỏc đ biºu thực (1.50). Đ phƯn tiáp theo, NCS s³ trỡnh bày phương phỏp xỏc đành yáu tố ma trên này dỹa trờn mău folding kộp. Đ°c biằt, viằc ỏp dửng tương tỏc NN hiằu dửng cú tớnh đán đúng gúp số hÔng tỏi ch¿nh hủp (Rearrangment term, viát tưt là RT) vào mău folding kộp đưủc nhĐn mÔnh.
29
30 Chương 1 Cơ sđ lý thuyát mụ tÊ tỏn xÔ hÔt nhõn-hÔt nhõn
1.4.1 Mău folding kộp
sau
Ta cú yáu tố ma trên tương tỏc đ biºu thực (1.50) đưđc khai triºn như
LiIi
LjIj
X
hLiIiJ|V |LjIjJi = ZdRˆdx hΦJ MJ(Rˆ, x)i∗V (R)ΦJ MJ(Rˆ, x)
=
MiMj ,MIi MIj
hLiMi, IiMIi |JMJihLjMj, IjMIj |JMJi ì
LiMi
LjMj
Ii
Ij
ZdRˆhiLiY
(Rˆ)i∗hiLjY (Rˆ)ihψMIi|V (R)|ψMIji, (1.57)
Ii Ij
M M
Ii
Ij
vỵi i, j = β ho°c γ. Đ biºu thực trờn, yáu tố ma trên hψ |V (R)|ψ i
chựa tĐt cÊ cỏc thụng tin vã cĐu trỳc hÔt nhõn thụng qua cỏc hàm súng nởi
ψ , ψ
MIi MIj
cơa hằ cũng như tương tỏc hÔt nhõn V (R). Yáu tố ma trên này
IiIj
t¿ lằ vợi
MIi
MIj
Mpi
Mti
Mpj
Mtj
vỵi ψMp , ψMt
hψIi|V (R)|ψIji ∼ hψIpiψIti|V (R)|ψIpiψItji, (1.58)
lƯn lưủt là hàm súng nởi cơa hÔt nhõn bưn tợi và hÔt nhõn bia.
Ip It
Cũng cƯn lưu ý rơng vợi i = j, yáu tố ma trên tương tỏc đ vá phÊi cơa phương
trình (1.58) chớnh là thá quang hồc, trong khi vợi i 6= j là thá dàch chuyºn. Đối vợi cỏc chương trỡnh chuân tớnh tỏn xÔ như ECIS [44], Fresco [45] vv..., thụng tin cơ bÊn chỳng ta cƯn đưa vào cỏc chương trỡnh là thá quang hồc và thá dàch chuyºn này. Cú nhiãu mụ hỡnh khỏc nhau tớnh OP và thá dàch chuyºn. Trong luên ỏn này, NCS sỷ dửng mău folding kộp đº tớnh toỏn yáu cỏc thá này vợi thụng số đƯu vào là hàm súng nởi cơa hÔt nhõn tợi, hÔt nhõn bia và tương tỏc NN hiằu dửng. Trong mău folding, tương tỏc V đưủc xem là tờng tương tỏc NN hiằu dửng giỳa nucleon k trong hÔt nhõn bưn tợi (p) và nucleon l trong hÔt nhõn bia (t).
X
V =
k∈p,l∈t
(vkl + iwkl), (1.59)
30
Chương 1 Cơ sđ lý thuyát mụ tÊ tỏn xÔ hÔt nhõn-hÔt nhõn
trong đó vkl, wkllƯn lưủt là phƯn thỹc và phƯn Êo cơa tương tỏc NN hiằu dửng. Trong luên ỏn này, chỳng tụi ch¿ têp trung vào tớnh toỏn thá tương tỏc hÔt nhõn-hÔt nhõn vợi phƯn thỹc vkl cơa tương tỏc NN hiằu dửng. Đối vợi phƯn Êo, chỳng tụi sỷ dửng thá hiằn tưủng luên WS cho OP. Bđi vỡ cỏc nucleon là cỏc fermion, chỳng phÊi thọa món nguyờn lý Pauli vợi yờu cƯu hàm súng cơa hằ phÊi phÊn xựng khi hoỏn đời giỳa nucleon k và nucleon l.
Điãu này dăn đán tương đương thay
x σ τ D EX x
kl
kl
kl
kl
vkl → vkl(1 − Pkl) = vkl(1 − P P P ) = v + v P , (1.60)
trong đó
vD = vkl và vEX = −P σ P τ vkl. (1.61)
kl
ij
Đ đây Pkl = P x P σ P τ là toỏn tỷ hoỏn đời giỳa c°p nucleon k, l, vỵi P x ,
kl kl kl kl
P
kl
kl
σ và P τ
lƯn lưủt là toỏn tỷ hoỏn đời khụng gian, spin và spin đỗng và cơa
Mpi Mti Mpj Mtj
c°p nucleon tương ựng. Như vêy, yáu tố ma trên hψ ψ |V (R)|ψ ψ i
đưđc khai triºn như sau [46–48]
Ipi
Iti
Ipi
Itj
Mpi
Mti
Mpj
Mtj
l∈t h
i i D j j
i i EX x
j j i
X
hψIpi ψIti |V (R)|ψIpi ψItj i =
k∈p
hϕkϕl |v
|ϕkϕli + hϕkϕl|v
|Pkl(ϕkϕl )i
hay U ij= U D(E, R) + U EX(E, R, R0), (1.62)
F ij ij
ij
vỵi ϕk và ϕl lƯn lưủt là cỏc hàm súng đơn hÔt nucleon thuởc hÔt nhõn bưn tợi và hÔt nhõn bia. Ta cú thành phƯn thá trỹc tiáp U D(E, R) là đành xự (ch¿ phử thuởc bián R) và cú thº đưủc viát lÔi dượi dÔng
ij
p
t
U D(E, R) = Z ρij (rp)ρij (rt)vD(E, ρ, s)drpdrt, (1.63) trong đó s = rt − rp + R, mối liờn hằ cỏc tồa đở này đưủc mụ tÊ đ Hỡnh 1.1,
p
p
ρij (rp) ≡ ρij (rp, rp) là mêt đở cơa cơa hÔt nhõn bưn tợi đưủc xỏc đành theo
cỏc hàm súng đơn hÔt dượi dÔng tờng quỏt như sau
31
32 Chương 1 Cơ sđ lý thuyát mụ tÊ tỏn xÔ hÔt nhõn-hÔt nhõn
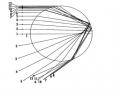
Hình 1.1: Mối liờn hằ cỏc tồa đở đưủc sỷ dửng trong mău folding kộp, rp và rt lƯn lưủt là vecto bỏn kớnh cơa nucleon đ trong hÔt nhõn bưn tợi và hÔt nhõn bia.
p
p
k
k
p
ρij(rp, r0) = Xhϕi(rp)i∗ϕj(r0). (1.64)
k∈p
Tương tỹ như vêy ta cũng cú mêt đở cho hÔt nhõn bia
t
t
l
l
t
ρij(rt, r0) = Xhϕi(rt)i∗ϕj(r0). (1.65)
l∈t
l∈t
ij
Đối vợi thành phƯn thá trao đời U EX(E, R, R0), do hoỏn đời và trớ cơa hai nucleon k, l làm thay đời khối tõm cơa hÔt nhõn bưn tợi và hÔt nhõn bia, dăn đán tồa đở nối giỳa hai khối tõm bà thay đời tứ R → R0, do đú, thành phƯn thá trao đời là phi đành xự (phử thuởc đỗng thới R, R0). Viằc này dăn đán phương trỡnh Schodinger trđ thành phương trỡnh vi tớch phõn và gõy khú khăn trong giÊi bài toỏn tỏn xÔ. Thay vào đú thành phƯn này cú thº xĐp x¿ vã đành xự bơng cỏch xỷ lý hàm súng chuyºn đởng tương đối như súng ph¯ng [46–48]. Khi đú thành phƯn thá trao đời đưủc đưa vã dượi dÔng đành xự như sau
ij
p
t
U EX(E, R) = Zρij (rp, rp + s)ρij (rt, rt − s)vEX(E, ρ, s)
M
p
× exp "iK(R)s# dr
drt. (1.66)
32
Chương 1 Cơ sđ lý thuyát mụ tÊ tỏn xÔ hÔt nhõn-hÔt nhõn
Đ đây K(R) là xung lưủng cơa chuyºn đởng tương đối hai hÔt nhõn, vợi
~2
F
K2(R) = 2µE − U
(E, R) − V
(R), (1.67)
C
M = MpMt/(Mp+ Mt) là số khối rỳt gồn, vợi Mp, MtlƯn lưủt là số khối cơa hÔt nhõn bưn tợi và bia. Ngay cÊ khi đưa thành phƯn thá trao đời vã đành xự, thành phƯn này văn phực tÔp do đưủc xỏc đành tỹ hủp khi U EXphử thuởc vào K(R) như đ (1.66) và K(R) lÔi phử thuởc vào U EXtheo hằ thực (1.67) vỵi UF= U D+ U EX. Do đú đº đơn giÊn tớnh toỏn, thành phƯn mêt đở đ (1.66) cũng đưủc xĐp x¿ vã dÔng đơn giÊn hơn [46–48]
+ ) 2
ρ(r, r + s) = ρ(r
sˆj "k
r + ss# , (1.68)
1
F
2
ij
vỵi ˆj1(x) = 3(sin x − x cos x)/x3, kFlà mụ men xung lưủng Fermi đưủc chồn nhơm tăng đở chớnh xỏc cơa xĐp x¿ trờn. Thay biºu thực (1.68) vào (1.66), ta cú thº đưa biºu thực thành phƯn thá trao đời U EX(E, R) vã dượi dÔng
đơn giÊn hơn như sau
U (E, R) = 4π Z v (E, ρ, s)j
EX ∞EX
ij0
0
K(R)s/Ms2ds
vỵi
× Zfp(r, s)ft(r − R, s)dr. (1.69)
sin x
j0(x) =
x
và f
p(t)
(r, s) = ρij
(r)ˆj1
hkFp(t)
(r) si . (1.70)
p(t)
Thành phƯn thá trao đời đưủc xỏc đành bơng phương phỏp l°p, vợi giỏ trà ban đƯu U EX đưủc cho bơng 0 đº tớnh K(R) đ (1.67), sau đó giá trà K(R) đưủc thá ngưủc vào đ (1.66) đº tính U EX, cỏc bược đưủc thỹc hiằn đán khi U EX hởi tử. Như vêy đº tớnh thá tương tỏc hÔt nhõn-hÔt nhõn theo mău folding, ta cƯn thụng số đƯu vào tương tỏc NN hiằu dửng (biºu thực (1.59)) và mêt đở hÔt nhõn đưủc xỏc đành theo biºu thực (1.64) và (1.65). Nởi dung tiáp theo NCS s³ trỡnh bày cỏc phương phỏp xỏc đành mêt đở hÔt nhõn và
33