Một Số Ứng Dụng Thực Tế Của Bài Toán Ms-Rcpsp

Ei Ej - tj WjW, j1, WiCj (1.6)

𝑞

∀ W𝑖 ∈ 𝑊𝑘 ∃ 𝑆𝑞 ∈ 𝑆𝑘 ∶ 𝑔𝑆

= 𝑔𝑟𝑖 và ℎ𝑆𝑞

≥ ℎ𝑟𝑖 (1.7)

𝑖=1

∀ 𝐿𝑘 ∈ 𝐿, ∀𝑞 ∈ 𝑚 ∶ ∑𝑛

𝑞

𝐴

𝑖,𝑘

≤ 1 (1.8)

∀ 𝑊𝑗 ∈ 𝑊 ∃! 𝑞 ∈ [0, 𝑚], ! 𝐿𝑘 ∈ 𝐿: 𝐴𝑞 = 1; với 𝐴𝑞 ∈ {0; 1} (1.9)

Cụ thể:

𝑗,𝑘

 Ràng buộc (1.3): mỗi tài nguyên phải có tối thiểu một kỹ năng nào đó

 Ràng buộc (1.4, 1.5): thời gian thực hiện của tác vụ bất kỳ tối thiểu phải bằng 0 (thực tế thì mọi tác vụ thật, có thời gian thực hiện tối thiểu luôn > 0, trường hợp bằng 0 để minh họa cho 2 tác vụ giả thể hiện thời điểm bắt đầu và kết thúc của dự án)

 Ràng buộc (1.6): tác vụ cha (task i) phải kết thúc trước thời điểm tác vụ con (task j) bắt đầu. Thời điểm tác vụ i kết thúc ký hiệu là Ei, thời điểm tác vụ con j bắt đầu là Ej - tj (thời điểm kết thúc trừ đi thời gian thực hiện).

 Ràng buộc (1.7) nghĩa là: với mọi tác vụ i  Wk (tập các tác vụ mà tài nguyên k thực hiện được), luôn tồn tại kỹ năng S  Sk (tập skill của tài nguyên k) sao cho 𝑔𝑆 = 𝑔𝑆𝑖: loại skill của r trùng với loại kỹ năng của Li mà tác vụ i yêu cầu. ℎ𝑆𝑞 ≥ ℎ𝑟𝑖 : mức kỹ năng của tài nguyên thực hiện cao hơn hoặc bằng mức kỹ năng yêu cầu.

 Ràng buộc (1.8): tại mỗi thời điểm (q), mỗi tài nguyên chỉ được thực hiện

𝑖=1

𝑖,𝑘

tối đa một tác vụ. Nếu ∑𝑛 𝐴𝑞 = 0 thì tài nguyên k không được gán cho

𝑖=1

tác vụ nào, nếu ∑𝑛

𝑞

𝐴

𝑖,𝑘

=1 thì tài nguyên k được gán cho một tác vụ duy

nhất.

 Ràng buộc (1.9): mỗi tác vụ chỉ được gán cho một tài nguyên duy nhất và chỉ được thực hiện bởi một tài nguyên duy nhất.

Trong bài toán MS-RCPSP, mỗi tác vụ có thêm các yêu cầu về kỹ năng (skill) của tài nguyên cần để thực hiện, mỗi tài nguyên cũng được chia làm nhiều mức kỹ năng khác nhau. Các ràng buộc về kỹ năng của tài nguyên được

 Có thể thiết lập

 Không thể thiết lập

Tác vụ

Tài nguyên

yêu cầu để thực hiện một tác vụ được mô tả dưới dạng một ma trận như ví dụ được minh họa trong hình 1.3 dưới đây:

S2.2

S3.1	S2.2	S1.1
W1	W2	W3	W4

Có thể bạn quan tâm!

Xem toàn bộ 156 trang tài liệu này.

S1.3, S2.2	L1
S2.1, S3.2	L2
S1.2, S2.1	L3
S2.2, S3.3	L4

			
			
			
			

Hình 1.3. Ma trận quan hệ giữa tác vụ và kỹ năng của tài nguyên

Trong hình 1.3, ký hiệu: Si.j nghĩa là kỹ năng Si và mức kỹ năng j. Tác vụ yêu cầu tài nguyên thực hiện phải đáp ứng loại kỹ năng và mức kỹ năng cụ thể. Tài nguyên thực hiện cần có cùng loại kỹ năng và mức kỹ năng lớn hơn hoặc bằng mức kỹ năng yêu cầu.

Cụ thể:

Tác vụ W1, yêu cầu tài nguyên có loại kỹ năng S2 và mức kỹ năng lớn hơn hoặc bằng 2. Đối chiếu với bảng tài nguyên, ta thấy tài nguyên L1 có loại kỹ năng S2 và mức kỹ năng của S2 là 2, do vậy L1 có thể thực hiện W1.

1.1.2. Một số ứng dụng thực tế của bài toán MS-RCPSP

1.1.2.1. Ứng dụng trong Fog Computing và Edge Computing

Fog Computing [32] được thiết kế để khắc phục những hạn chế của điện toán đám mây (Cloud Computing) bằng cách cung cấp một kiến trúc phân tán trong đó một số dữ liệu sẽ được phân loại để xử lý ngay bởi các thiết bị ở gần nơi phát sinh dữ liệu thay vì phải gửi về trung tâm đám mây, như vậy vừa tiết kiệm được chi phí truyền thông, giảm khả năng bị mất mát hoặc rò rỉ (do vấn đề bảo mật) trên đường truyền lại vừa tránh được nghẽn đường truyền mạng. Những kiến trúc này được thiết kế và xây dựng theo các mô hình của Edge

Computing (Điện toán biên).

Nhiệm vụ chính của Fog Computing là tìm phương án bố trí các nguồn tài nguyên tính toán bao gồm máy chủ, router, các thiết bị lưu trữ, database sao cho tối đa hóa việc truy xuất và xử lý cục bộ. Nói cách khác, cần tìm cách sắp xếp sao cho chỉ những tác vụ đặc thù (chẳng hạn yêu cầu nhiều tài nguyên) mới phải gán cho các tài nguyên ở đám mây trung tâm (vốn ở rất xa khách hàng), còn những tác vụ có thể giải quyết tại chỗ thì đều được gán cho những nguồn tài nguyên ngay tại nơi phát sinh yêu cầu (chẳng hạn các máy chủ có sẵn trong mạng LAN của khách hàng). Làm như vậy vừa giảm bớt được chi phí thực thi (có lợi cho khách hàng), bao gồm chi phí truyền thông tin và chi phí xử lý dữ liệu, vừa giảm bớt được tình trạng tắc nghẽn đường truyền trong những giờ cao điểm (có lợi cho nhà cung cấp dịch vụ), lại có thể rút ngắn thời gian xử lý để đáp ứng yêu cầu về thời gian thực của một số ứng dụng. Các giải pháp lập lịch dựa trên bài toán RCPSP có thể được áp dụng trong trường hợp này [CT4]. Việc lập lịch trong môi trường Fog Computing được chia làm 3 nhóm:

- Lập lịch cấp phát tài nguyên (resource scheduling)

- Lập lịch quản lý luồng công việc (workflow scheduling)

- Lập lịch quản lý các tác vụ (task scheduling)

1.1.2.2. Ứng dụng trong các ngành kinh tế Vấn đề "giá tùy chọn" (Option Pricing Problem)

Mô hình định giá tùy chọn [11], [62] là mô hình toán học sử dụng các biến nhất định để tính toán giá trị lý thuyết của một tùy chọn. Một tùy chọn hiểu là một hợp đồng hai bên trong việc thực hiện một giao dịch. Có hai loại tùy chọn chính:

- Call: là hợp đồng tùy chọn cung cấp cho bạn quyền nhưng không phải là nghĩa vụ mua tài sản ở mức giá đã xác định trước hoặc vào ngày hết hạn.

- Put: là hợp đồng tùy chọn cung cấp cho bạn quyền nhưng không phải là nghĩa vụ bán tài sản ở mức giá đã xác định trước ngày hết hạn.

Giá tùy chọn là nội dung cốt lòi của tài chính hiện đại, được áp dụng trong thị trường chứng khoán hoặc trong thị trường tài chính nói chung.

Vấn đề thị trường chứng khoán (Stock Problem)

Black and Scholes đã đề xuất mô hình Black-Scholes[11] áp dụng trong thị trường chứng khoán, sau đó mô hình tính toán này được sử dụng để tính toán trong lĩnh vực tài chính khác. Ngày nay mô hình này trở thành một công cụ không thể thiếu trong thị trường chứng khoán và thị trường tài chính.

Vấn đề vị trí thiết lập kho (Facility Location Problem)

Mục tiêu là tìm kiếm vị trí đặt các kho hàng (chi nhánh) trong mạng (chuỗi) sao cho tối thiểu hóa chi phí vận chuyển đồng thời xem xét đến các yếu tố ràng buộc như: đối thủ cạnh tranh, không đặt gần các vị có thể gây nguy hiểm như cháy nổ. Bài toán này đã được Y Gao[62] đề xuất dựa trên lý thuyết không chắc chắn.

1.1.2.3. Ứng dụng trong lĩnh vực quân sự

Một bài toán con của RCPSP, ký hiệu là SRCPSP (Stochastic Resource- constrained Project Scheduling) [17], được áp dụng trong quân sự ở ba trường hợp cụ thể sau.

Lập kế hoạch nhiệm vụ (Mission Planning)

Một nhiệm vụ quân sự có thể được mô hình hóa như một dự án bao gồm một hệ thống phân cấp công việc khác nhau. Các tài nguyên bao gồm: nhân lực, tài liệu, thiết bị cần thiết để hoàn thành nhiệm vụ. SRCPSP đã được áp dụng thành công để lập lịch thực hiện các tác vụ trên tàu hải quân [18].

Bảng 1.2: Dữ liệu về tác vụ và yêu cầu thực hiện

Tác

vụ

Thời gian thực hiện (giờ)	Kỹ năng cần thiết	Thứ tự thực hiện	Thời hạn (giờ)
J1	13	[0,1,0,0]		15
J2	6	[0,0,1,0]		40
J3	7	[1,0,0,0]		20
J4	9	[0,0,0,1]		30
J5	13	[0,1,0,0]		50
J6	11	[0,0,1,0]		60
J7	8	[1,0,0,0]		50
J8	12	[1,1,0,0]	-	60
J9	13	[0,0,1,0]	-	40
J10	15	[0,0,1,0]	-	50

Bảng 1.2 thể hiện rằng trên tàu hải quân có 10 công việc(Job) cần thực hiện, từ J1 đến J10, mỗi tác vụ có thời gian xử lý và yêu cầu kỹ năng nhất định đối với thủy thủ. Biểu diễn thể hiện công việc 9 chỉ bắt đầu sau khi công việc 1 bắt đầu được 14 giờ, các thủy thủ có thể có một hoặc nhiều kỹ năng trong tập {K1, K2, K3, K4}, Áp dụng thuật toán xếp lịch, với 4 thủy thủ, kết quả được thể hiện trong sơ đồ Gantt như hình 1.4 dưới đây.

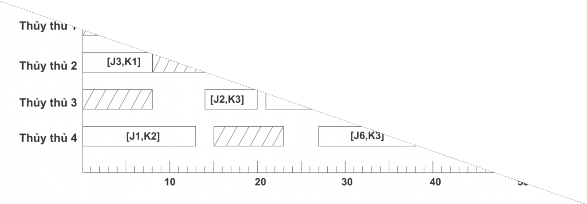
Hình 1.4. Biểu đồ Gantt mô tả một phương án lịch biểu.

Lập kế hoạch dẫn đường

Bài toán Lập kế hoạch dẫn đường (Shortest Path Problem - SPP) nhằm tìm đường đi ngắn nhất từ nguồn tới đích với chi phí thực hiện thấp nhất [28]. SPP được áp dụng trong việc dẫn đường cho thiết bị bay không người lái (UAV - Unmanned Aerial Vehicle) đến một đích cụ thể thông qua một tuyến đường

ngắn nhất và khả năng thành công bay đến đích cao nhất, chẳng hạn đảm bảo 2 UAV không va chạm nhau trên lịch trình. Hành trình của UAV cần đảm bảo thỏa mãn các ràng buộc về khả năng sống sót, các ràng buộc vật lý, cảm biến và các hoạt động khác. SPP chính là một nhánh của bài toán RCPSP.

Hình 1.5 mô tả tuyến đường và khả năng tính toán thông qua cảm biến của hai UAV nhằm đảm bảo không va chạm trong quá trình thực hiện chuyến bay [28].

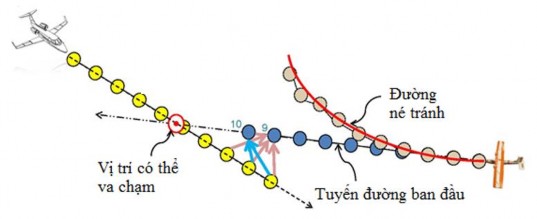
Hình 1.5. Sơ đồ bay của 2 chiếc UAV

Thiết lập mạng vận chuyển hậu cần (Configuring Logistics Networks)

Năm 2005, Bộ Quốc phòng Mỹ xác định xây dựng chuỗi cung ứng vật tư quân trang trong quân đội là 1 trong 25 nhiệm vụ trọng điểm của quân đội [13]. Với yêu cầu đó, quân đội Mỹ đã xây dựng mạng vận chuyển hậu cần quân sự nhằm giảm thiểu thời gian cấp phát trang thiết bị đến các vị trí đóng quân tại các vị trí khác nhau đồng thời kiểm soát lượng vật tư còn tồn trong kho. Bài toán RCPSP [2],[46] được nghiên cứu ứng dụng trong việc lên kế hoạch vận chuyển trong mạng hậu cần quân sự theo mô hình trên.

1.1.3. Những nghiên cứu liên quan

Như phần trước đã giới thiệu, bài toán lập lịch với tài nguyên giới hạn và đa kỹ năng MS-RCPSP có nhiều ứng dụng trong khoa học và thực tiễn nên đã

được nghiên cứu rộng rãi bởi nhiều nhà khoa học và đã có nhiều công bố khoa học liên quan đến bài toán này. MS-RCPSP đã được chứng minh là bài toán thuộc lớp NP-Khó [2],[22],[46] nên các nhóm tác giả đều sử dụng các phương pháp tìm lời giải gần đúng.

Myszkowski và cộng sự [42],[45] là nhóm nghiên cứu tập trung vào bài toán MS-RCPSP trong nhiều năm, họ công bố sớm và nhiều kết quả về bài toán này. Ban đầu nhóm của Myszkowski giải quyết MS-RCPSP bằng các heuristic [31],[43],[44], chẳng hạn như bố trí thứ tự thực thi các tác vụ dựa trên thời lượng của chúng. Các tác vụ được sắp xếp theo thời lượng tăng dần, sau đó tài nguyên được gán cho chúng theo thứ tự đó. Nếu có nhiều tài nguyên phù hợp với một tác vụ thì tài nguyên rẻ nhất sẽ được chọn.

Sau đó, theo xu hướng chung, Myszkowski và cộng sự nhận ra rằng các heuristic thiếu ổn định và có phạm vi ứng dụng hẹp so với các metaheuristic nên đã chuyển sang nghiên cứu các thuật toán tiến hóa. Họ đã công bố các công trình giải quyết bài toán MS-RCPSP trong đó sử dụng:

- Thuật toán Tabu Search [31];

- Thuật toán Đàn kiến [44];

- Thuật toán GA [43];

- Một số thuật toán khác

So với các thuật toán đã công bố, đóng góp lớn nhất của Myszkowski và cộng sự là đã xây dựng và công bố bộ dữ liệu chuẩn iMOPSE [42]. Trong khi các nhóm nghiên cứu trước đó, chẳng hạn [51], thường sử dụng bộ dữ liệu PSPLIB [47] khi giải quyết bài toán RCPSP tổng quát, Myszkowski chỉ ra rằng bộ dữ liệu này thiếu trường thông tin về chi phí thực hiện tác vụ, do đó không hoàn toàn thích hợp với bài toán MS-RCPSP. Nhóm của Myszkowski đã tự xây dựng và công bố bộ dữ liệu chuẩn iMOPSE [42], sau này được công nhận rộng rãi và được nhiều nhóm nghiên cứu cũng như chính luận án này sử dụng.

Qua các công trình công bố, có thể thấy, trong các nghiên cứu của mình, nhóm tác giả Myszkowski sử dụng các thuật toán truyền thống như GA, Greedy, Ant,... Luận án đặt mục tiêu tìm ra các thuật toán Metaheuristic mới để giải bài toán MS-RCPSP và các thực nghiệm được thực hiện trên bộ dữ liệu iMOPSE.

Một nhóm nghiên cứu bài toán MS-RCPSP lâu năm khác là nhóm của Hosseinian [4],[5],[6],[7]. Năm 2018, Hosseinian và Baradaran công bố kết quả nghiên cứu [4] về bài toán Multi-mode Multi-skilled Resource-Constrained Project Scheduling Problem (MMSRCPSP), một biến thể của bài toán MS- RCPSP trong đó bổ sung thêm ràng buộc rằng mỗi tác vụ chỉ có thể được thực thi ở một vài chế độ (mode) định trước và không thể thay đổi mode một khi quá trình thực thi đã được bắt đầu. Để giải quyết bài toán, Hosseinian và cộng sự đã sử dụng thuật toán GA cổ điển kết hợp với phương pháp ra quyết định dựa trên độ đo thông tin Shanon-entropy để lựa chọn cá thể cho thế hệ kế tiếp. Thực nghiệm được tiến hành trên bộ dữ liệu sinh ngẫu nhiên bởi phần mềm ProGen. Tiếp tục hướng nghiên cứu đó, năm 2019 nhóm tác giả này công bố bài báo [5] trong đó sử dụng thuật toán Dandelion Algorithm để giải quyết bài toán MS- RCPSP. Dandelion [53] là thuật toán tiến hóa mới được công bố năm 2017, lấy ý tưởng từ khả năng tự thay đổi bán kính và hướng gieo hạt của cây Bồ công anh. Trong bài này nhóm tác giả lựa chọn thực nghiệm trên iMOPSE [42], bộ dữ liệu chuẩn được công nhận rộng rãi, đa dạng và phù hợp hơn với bài toán MS-RCPSP. Năm 2020, nhóm tác giả này tiếp tục công bố bài báo [6] giải quyết bài toán MS-RCPSP đa mục tiêu với hai hàm mục tiêu là thời gian và chi phí thực hiện dự án. Nhóm tác giả sử dụng thuật toán Pareto-based Grey Wolf Optimizer và tiếp tục kiểm chứng các kết quả trên bộ dữ liệu chuẩn iMOPSE [42].

Qua phân tích tổng quan trên có thể thấy cách tiếp cận của Hosseinian và