Xếp Loại Bài Toán Real-Rcpsp Thông Qua Phân Loại Graham

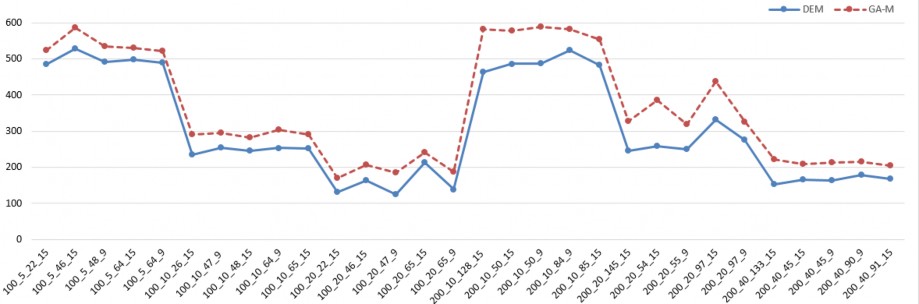
Hình 2.14. So sánh giá trị AVG giữa DEM với GA-M

Kết luận chương 2

Bài toán MS-RCPSP là bài toán có nhiều ứng dụng trong thực tế và đã được chứng minh là bài toán thuộc lớp NP-Khó, nên không thể tìm được nghiệm chính xác trong thời gian chấp nhận được. Để giải bài toán này, cần có các thuật toán cận tối ưu để tìm các các lời giản tốt trong thời gian ngắn.

Trong chương này, luận án đã trình bày về cách mã hóa cá thể và thang đo độ chênh giữa hai cá thể, đây là cơ sở quan trọng cho các cải tiến tiếp theo. Để giải bài toán, 2 thuật toán mới đã được đề xuất gồm:

Thuật toán 1: M-PSO, là thuật toán được xây dựng trên cơ sở của thuật toán tối ưu bầy đàn với cải tiến mới là kỹ thuật di cư, kỹ thuật này giúp thoát khỏi cực trị địa phương và mở rộng không gian tìm kiếm của bài toán.

Thuật toán 2: DEM, là thuật toán được phát triển từ thuật toán tiến hóa vi phân (DE) để áp dụng cho bài toán MS-RCPSP. Cải tiến quan trọng của DEM là áp dụng hàm Reallocate để tái thiết lập tài nguyên thực hiện các tác vụ trong một lời giải, giúp bài toán mở rộng không gian tìm kiếm và hội tụ nhanh chóng. Thuật toán này đã được công bố trong công trình [CT7], [CT8].

Để kiểm chứng tính hiệu quả của M-PSO và DEM, luận án đã triển khai thực nghiệm với bộ dữ liệu iMOPSE và có đánh giá so sánh cụ thể sau mỗi phần thực nghiệm.

Kết quả nghiên cứu của chương này được công bố tại:

- Hội thảo quốc tế 6th NAFOSTED Conference on Information and Computer Science (NICS), Hanoi, Vietnam, pp. 73-76, 2019 [CT5].

- Tạp chí International Journal of Electrical and Computer Engineering (IJECE), (Q3), Vol. 8, No. 5, pp. 3851-3858, October 2018 [CT2];

- Tạp chí Scientific Programming (IF:1.28, Q3), Volume 2020, Article ID 8860384, 12, 2020 [CT8].

CHƯƠNG 3

BÀI TOÁN REAL-RCPSP

Mô hình bài toán MS-RCPSP bổ sung yếu tố kỹ năng và mức kỹ năng của tài nguyên, nên khi yêu cầu tài nguyên thực hiện tác vụ cũng cần chỉ ra loại kỹ năng và mức kỹ năng tối thiểu cần thiết để thực hiện. Việc điều chỉnh này giúp bài toán MS-RCPSP có thể áp dụng được vào một số lĩnh vực thực tế. Tuy nhiên, trong các mô hình sản xuất, cần có những yêu cầu cụ thể và chính xác hơn như với mỗi tác vụ, tài nguyên (công nhân) có mức kỹ năng (trình độ) cao hơn có thể hoàn thành công việc sớm hơn hoặc với chất lượng tốt hơn. Đây chính là nhược điểm của bài toán MS-RCPSP, bài toán này quy định thời gian thực hiện một tác vụ là như nhau với bất kỳ tài nguyên thực hiện nào. Để khắc phục hạn chế này của bài toán MS-RCPSP, luận án đã đưa ra mô hình bài toán Real-RCPSP với ràng buộc về thời gian thực hiện tác vụ thay đổi theo mức kỹ năng của tài nguyên thực hiện. Phần tiếp theo của chương 03, luận án sẽ trình bày các vấn đề sau:

Phần 3.1: Phát biểu bài toán mới Real-RCPSP. Đây là bài toán có khả năng ứng dụng cao trong thực tiễn do được bổ sung các ràng buộc về thời gian thực hiện liên quan đến mức kỹ năng của các tài nguyên.

Phần 3.2: Xếp loại bài toán Real-RCPSP.

3.1. Bài toán Real-RCPSP

Trong thực tế sản xuất, thông thường, nhân công (tài nguyên) có trình độ tay nghề (mức kỹ năng) cao hơn, thường hoàn thành công việc với thời gian ít hơn hoặc chất lượng tốt hơn hoặc cả hai. Do vậy, để áp dụng tốt hơn việc lập kế hoạch điều phối công việc, kế hoạch trong sản xuất kinh doanh. Luận án đề xuất một bài toán mới là Real-RCPSP. Bài toán này được phát triển dựa trên

cơ sở của bài toán MS-RCPSP và bổ sung thêm ràng buộc về mức kỹ năng của tài nguyên thực hiện. Tài nguyên thực hiện tác vụ có mức kỹ năng cao hơn mức kỹ năng yêu cầu thì thời gian hoàn thành tác vụ có thể nhanh hơn.

3.1.1. Phát biểu bài toán

Các ký hiệu:

Ci: tập tác vụ (task) cần thực hiện trước tác vụ i

S: tập tất các các kỹ năng của các tài nguyên; Si: Tập các kỹ năng của tài nguyên i, Si S;

Si: kỹ năng thứ i;

tjk: thời gian thực hiện tác vụ j bởi tài nguyên k, thời gian thực hiện cùng một tác vụ có thể khác nhau với tài nguyên thực hiện khác nhau.

L: tập các tài nguyên;

Lk: tập tài nguyên có thể thực hiện tác vụ k; Lk L

Li: tài nguyên thứ i

W: tập các tác vụ của dự án;

Wk: tập các tác vụ có thể thực hiện bởi tài nguyên k, Wk W

Wi: tác vụ thứ i

ri: tập các kỹ năng được yêu cầu để thực hiện tác vụ i. Một tài nguyên có thể thực hiện được tác vụ i nếu có kỹ năng giống với kỹ năng yêu cầu của tác vụ i và có mức kỹ năng lớn hơn hoặc bằng mức kỹ năng yêu cầu.

Bk, Ek: thời gian bắt đầu và thời gian kết thúc thực hiện tác vụ k

Au,vi: biến xác định tài nguyên v có đang thực hiện tác vụ u tại thời điểm i

hay không; 1: có, 0: không

hi: mức kỹ năng của kỹ năng (skill) i; gi: loại kỹ năng i;

m: makespan của lịch biểu

P: một lịch biểu khả thi của bài toán; Pall: Tập tất cả các lịch biểu

f(P): hàm mục tiêu, để tính makespan của P

n: số tác vụ, z: số tài nguyên

Mục tiêu của bài toán Real-RCPSP là tìm lịch biểu P sao cho: f(P)  min

lịch biểu tìm được cần thỏa mãn các ràng buộc sau:

Sk Lk L			(3.1)
tjk 0 WjW, LkL			(3.2)
Ej 0 WjW			(3.3)
Ei Ej - tj WjW, j1, WiCj			(3.4)
∀ W𝑖 ∈ 𝑊𝑘 ∃ 𝑆𝑞 ∈ 𝑆𝑘 ∶ 𝑔𝑆 = 𝑔𝑟 và	ℎ𝑆 ≥ ℎ𝑟		(3.5)
∀ 𝐿𝑘 ∈ 𝐿, ∀𝑞 ∈ 𝑚 ∶ ∑𝑛 𝐴𝑞 ≤ 1			(3.6)
∀ 𝑊𝑗 ∈ 𝑊 ∃! 𝑞 ∈ [0, 𝑚], ! 𝐿𝑘 ∈ 𝐿: 𝐴𝑞	= 1; với 𝐴𝑞	∈ {0; 1}	(3.7)

Có thể bạn quan tâm!

• Đánh Giá Chất Lượng Lời Giải Của Thuật Toán
• Phương Pháp Tái Thiết Lập Tài Nguyên Thực Hiện
• Đánh Giá Chất Lượng Lời Giải Của Thuật Toán
• Một số phương pháp gần đúng giải bài toán lập lịch với tài nguyên giới hạn - 13
• Ý Tưởng Của Phương Pháp Thích Nghi
• Đánh Giá Chất Lượng Lời Giải Của Thuật Toán

Xem toàn bộ 156 trang tài liệu này.

𝑞 𝑖 𝑞 𝑖

𝑖=1 𝑖,𝑘

𝑗,𝑘 𝑗,𝑘

𝑡𝑖𝑘 ≤ 𝑡𝑖𝑙 𝑣ớ𝑖 ℎ𝑘 ≤ ℎ𝑙 ∀ (𝑟𝑘, 𝑟𝑙) ∈ {𝑆𝑘 × 𝑆𝑙 } (3.8)

Cụ thể:

 Các ràng buộc (3.1 đến 3.7) được phát biểu tương tự như bài toán MS- RCPSP

 Ràng buộc (3.8): là ràng buộc riêng của bài toán Real-RCPSP, thể hiện tài nguyên thực hiện có mức kỹ năng (trình độ) lớn hơn yêu cầu của tác vụ, thì thời gian thực hiện có thể nhỏ hơn hơn thời gian chuẩn của tác vụ.

3.1.2. Những ứng dụng thực tế của bài toán Real-RCPSP

Cải tiến quan trọng của bài toán Real-RCPSP là sự điều chỉnh thời gian thực hiện mỗi tác vụ theo mức kỹ năng. Nếu xem xét cụ thể trong các dự án thực tế, thông thường với cùng một tác vụ, nhân công (tài nguyên) có trình độ cao sẽ hoàn thành trong thời gian ngắn hơn nhân công có trình độ thấp. Do vậy, bài toán Real-RCPSP có khả năng ứng dụng cao trong thực tiễn, một số lĩnh

vực cụ thể có thể áp dụng mô hình bài toán này là:

- Trong lĩnh vực sản xuất: thông thường các quy trình sản xuất thành phẩm sẽ thực hiện theo dây chuyền gồm nhiều công đoạn, mỗi công đoạn yêu cầu nhân công thực hiện với trình độ tay nghề khác nhau. Khi đó, bài toán Real- RCPSP sẽ căn cứ trên các tài nguyên sẵn có, đưa ra một kế hoạch sản xuất tốt, tiết kiệm tối đa thời gian thực hiện.

- Trong lĩnh vực logistic: bài toán này giúp lên kế hoạch, điều phối kho bãi, thiết bị giao vận một cách phù hợp theo các nhu cầu lưu kho, vận chuyển cụ thể, tránh lãng phí tài nguyên.

- Cấp phát tài nguyên trong các hệ thống công nghệ thông tin: tùy theo từng công việc cụ thể, nhu cầu sử dụng tài nguyên có thể khác nhau, các tài nguyên bao gồm: hệ thống máy chủ, hệ thống lưu trữ, lưu lượng mạng, khả năng xử lý, ... Bài toán Real-RCPSP có thể áp dụng một cách hiệu quả trong việc phân công, cấp phát tài nguyên theo từng yêu cầu cụ thể, trong các hệ thống IoT và nhiều lĩnh vực ứng dụng khác.

3.2. Xếp loại bài toán Real-RCPSP thông qua phân loại Graham

Lập lịch (Scheduling) là tên gọi chung để chỉ họ bài toán bao gồm rất nhiều nhánh với những đặc trưng đa dạng. Những trường hợp riêng, những bài toán con mới trong họ bài toán lập lịch không ngừng được các nhóm nghiên cứu đề xuất và nghiên cứu vì chúng xuất hiện trong mọi mặt của khoa học, công nghệ và đời sống. Họ bài toán lập lịch có nhiều lớp, nhiều bài toán con và nhiều biến thể khác nhau, nên cần được phân loại để thuận lợi trong việc so sánh, đối chiếu.

Năm 1979 Graham [51] đã đề xuất một cách phân loại cho các bài toán Lập lịch. Cách phân loại Graham, sau khi được Veltman [9] bổ sung vào năm 1990, được giới nghiên cứu công nhận và sử dụng một cách rộng rãi. Cách phân loại Graham khá đơn giản và dễ thực hiện, đồng thời cho phép biểu diễn tất cả

những yếu tố - vốn rất đa dạng và phức tạp của các bài toán - chỉ bằng ba thành phần ký hiệu là α|β|γ. Ngoài ra cách phân loại Graham (đôi khi còn được gọi là Ký pháp Graham) có thể được mở rộng để biểu thị hầu hết các bài toán con trong họ bài toán Lập lịch, nói cách khác gần như mọi bài toán Lập lịch đều có thể biểu diễn được bằng ký pháp Graham, hơn nữa cách biểu diễn đó lại rất ngắn gọn.

Để phân loại các bài toán lập lịch, Graham xem xét ba thành phần cơ bản mà bài toán lập lịch nào cũng có, đó là:

 α: thành phần đặc trưng cho tác vụ, mô tả những tác vụ mà hệ thống cần thực hiện.

 β: thành phần đặc trưng cho hệ thống đang cần lập lịch, mô tả những đặc trưng của hệ thống.

 γ: thành phần đặc trưng cho mục tiêu của việc lập lịch, cho biết đại lượng nào cần được tối ưu hóa.

Sau đó Veltman đề xuất và được giới nghiên cứu nhất trí sử dụng ba thành phần đó theo một thứ tự logic hơn như sau:

 Thành phần thứ nhất (α) mô tả những đặc trưng của hệ thống như: số lượng tài nguyên (trong trường hợp cụ thể, tài nguyên là các server, router, công nhân, robot...), năng lực tính toán của tài nguyên, cơ chế đồng bộ hóa và mạng kết nối giữa các tài nguyên.

 Thành phần thứ hai (β) mô tả các tính chất của tác vụ, công việc.

 Thành phần thứ ba (γ) chỉ ra mục tiêu của bài toán là gì, mô tả đại lượng cần được tối ưu hóa. Chẳng hạn như việc giải bài toán hướng đến việc tối thiểu hóa thời gian thực hiện, tối đa hóa lợi nhuận hay tối thiểu hóa chi phí.

Trong ký pháp Graham, mỗi thành phần là một hoặc một dãy ký hiệu ngăn cách nhau bởi dấu phẩy, các ký hiệu đó cho biết bài toán thuộc lớp bài toán con nào trong những trường hợp đã biết.

Thành phần thứ nhất (α)

Để biểu diễn những đặc trưng của hệ thống, thành phần thứ nhất bao gồm hai trường là Kiểu tài nguyên và Số lượng tài nguyên. Mỗi trường bao gồm những ký hiệu phản ánh những đặc trưng dưới đây.

Kiểu tài nguyên:

 1: hệ thống chỉ có một tài nguyên duy nhất

 P: hệ thống gồm nhiều tài nguyên giống hệt nhau về năng lực và chúng hoạt động song song với nhau.

𝑃̅: như trường hợp P song song bổ sung thêm giả thiết rằng số lượng tài

nguyên lớn hơn hoặc bằng số lượng tác vụ cần thực hiện.

 Q: hệ thống gồm những tài nguyên khác nhau về năng lực. Bài toán Real- RCPSP có đặc trưng này.

 MPM: mỗi tài nguyên có thể thực hiện bất cứ tác vụ nào hay bất cứ công đoạn nào của tác vụ trong trường hợp tác vụ bao gồm nhiều công đoạn.

 O: Bài toán Open Shop

 F: Bài toán Flow Shop

 J: Bài toán Job Shop

Số lượng tài nguyên:

 Để trống: số lượng tài nguyên thay đổi tùy theo giải pháp sử dụng. Bài toán Real-RCPSP có đặc trưng này.

 Một số nguyên dương m: các giải pháp bắt buộc phải sử dụng đúng m tài nguyên, m được quy định bởi giả thiết của bài toán.

 ∞: các giải pháp được sử dụng số lượng tài nguyên tùy ý, không giới hạn

Thành phần thứ hai (β):

Thành phần này mô tả các đặc trưng của tác vụ công việc phải thực hiện thông qua một hoặc nhiều trường con ngăn cách nhau bởi dấu phẩy. Các trường