Trang chủ

Phương Pháp Tái Thiết Lập Tài Nguyên Thực Hiện


của M-PSO là 85,3. Từ kết quả này, có thể thấy, thuật toán M-PSO mang lại hiệu quả cao hơn thuật toán GA-M và tính ổn định của M-PSO cũng tốt hơn.

So sánh với các thuật toán lai (hybrid) khác


- Bảng 2.13 cho thấy, kết quả của M-PSO có kết quả tốt hơn các thuật toán lai ở hầu hết các trường hợp, cụ thể: tốt hơn HAntCO 29/30 bộ dữ liêu, tốt hơn GRASP 27/30 bộ dữ liệu với giá trị BEST, 26/30 bộ dữ liệu với giá trị AVG. Một số trường hợp M-PSO kém hơn các thuật toán lai, tuy nhiên, giá trị kém hơn không nhiều. Ví dụ, khi so sánh với thuật toán GRASP, trường hợp kém nhất của M-PSO so với GRASP là -7.04%, trong khi đó giá trị tốt nhất cao hơn GRASP là 15.79%.

Như vậy, trong thuật toán mới M-PSO với việc bổ sung phương pháp di cư quần thể đã mang lại hiệu quả tốt cho thuật toán. Bản chất của việc di cư quần thể là việc mở rộng không gian tìm kiếm, giúp thuật toán có khả năng quét và duyệt được nhiều phương án hơn, do vậy có khả năng tìm được nghiệm tốt hơn. Ngoài ra, phương pháp di cư giúp thuật toán mới dễ dàng thoát khỏi cực trị địa phương.

63


2.3.5. Hình ảnh so sánh M-PSO và GA-M


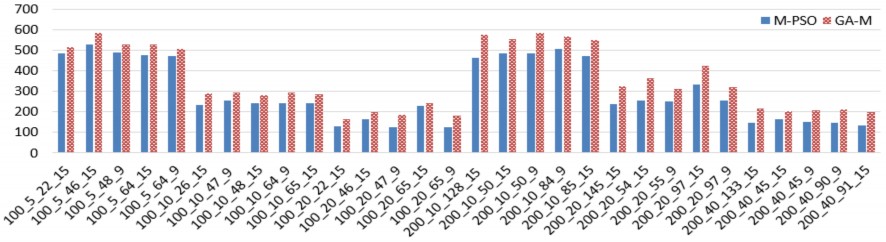
Hình 2 5 So sánh giá trị BEST giữa M PSO và GA M Hình 2 6 So sánh giá trị STD giữa 1

Hình 2.5. So sánh giá trị BEST giữa M-PSO và GA-M

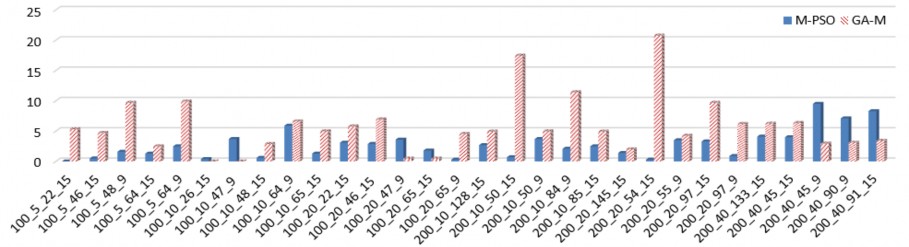
Hình 2 6 So sánh giá trị STD giữa M PSO và GA M 2 4 Đề xuất thuật toán DEM 2

Hình 2.6. So sánh giá trị STD giữa M-PSO và GA-M


2.4. Đề xuất thuật toán DEM


Thuật toán DEM (Reallocate Differential Evolution for MS-RCPSP) [CT7], [CT8] được xây dựng trên cơ sở là thuật toán DE để giải bài toán MS- RCPSP. Mục tiêu của thuật toán này là tìm ra được lịch biểu với thời gian thực hiện ngắn nhất. DEM áp dụng cho MS-RCPSP với cải tiến như sau:

Với cá thể tốt nhất sau mỗi thế hệ, áp dụng phương pháp tìm và thay thế tài nguyên thực hiện các tác vụ của cá thể. Phương pháp này được gọi là tái thiết lập tài nguyên thực hiện.

2.4.1. Phương pháp tái thiết lập tài nguyên thực hiện


2.4.1.1. Ý tưởng của phương pháp tái thiết lập


Trong bài toán MS-RCPSP, một lịch biểu là một cá thể biểu diễn tài nguyên thực hiện tác vụ thỏa mãn các ràng buộc ban đầu. Sau mỗi thế hệ, thuật toán sẽ tìm ra được lịch biểu tốt nhất (Cbest), dựa trên lịch biểu này, thực hiện tiếp thay đổi các tài nguyên thực hiện từng tác vụ sao cho vẫn đảm bảo được ràng buộc của bài toán. Việc thay đổi tài nguyên thực hiện tác vụ được gọi là phương pháp tái thiết lập (Reallocate). Phương pháp này giúp mở rộng được không gian tìm kiếm và có thể tránh được cực trị địa phương.

Phương pháp tái thiết lập được thực hiện qua các bước như sau:


- Bước 1: Tìm tài nguyên sử dụng nhiều nhất trong Cbest, gọi là Lb. Đây là tài nguyên kết thúc công việc sau cùng trong các tài nguyên sử dụng để thực hiện dự án.

- Bước 2: Duyệt lần lượt từng tác vụ được thực hiện bởi tài nguyên Lb theo thứ tự ưu tiên thực hiện của các tác vụ trên lịch biểu.

WRb: tập tác vụ đang được thực hiện bởi Lb

- Bước 3: Với mỗi tác vụ Wi ∈ WRb (i=1- sizeof(WRb)), thực hiện:


• Tìm tất cả các tài nguyên có khả năng thực hiện được tác vụ Wi khác với tài nguyên hiện tại (Lb), ký hiệu là LW;

• Duyệt lần lượt từng tài nguyên có thể thực hiện tác vụ Wi, với mỗi tài nguyên LjW ∈ LW, thực hiện:

o (1) Thiết lập tài nguyên thực hiện Wi là RjW;

o (2) Xóa Wi khỏi danh sách tác vụ mà là Lb đang thực hiện.

Sau (1) và (2) ta sẽ nhận được lịch biểu mới, tính makespan của lịch biểu mới newbest, nếu tốt hơn makespan của Cbest, thay thế Cbest bằng lịch newbest và dừng lại, nếu không, tiếp tục thực hiện vòng lặp để kiểm tra.

𝐶𝑏𝑒𝑠𝑡

{ 𝑛𝑒𝑤𝑏𝑒𝑠𝑡 𝑖𝑓 𝑓(𝑛𝑒𝑤𝑏𝑒𝑠𝑡 ) < 𝑓(𝐶𝑏𝑒𝑠𝑡)

𝐶𝑏𝑒𝑠𝑡 𝑖𝑓 𝑓(𝑛𝑒𝑤𝑏𝑒𝑠𝑡) ≥ 𝑓(𝐶𝑏𝑒𝑠𝑡)


Phép dịch chuyển này giúp thuật toán mở rộng không gian tìm kiếm bằng việc tạo ra các cá thể mới dựa trên cá thể tốt nhất. Do cá thể newbest được tạo ra từ cá thể tốt nhất nên có khả năng sử dụng được kinh nghiệm của cả quần thể và của cá thể tốt nhất qua các thế hệ, đây chính là đặc tính của thuật toán DE. Do vậy, sau khi áp dụng Reallocate, chúng ta có thể nhận được các cá thể tốt hơn.

2.4.1.2. Sơ đồ thuật toán


Các bước thực hiện của phương pháp tái thiết lập được thể hiện chi tiết trong sơ đồ thuật toán hình 2.7.

2.4.1.3. Hàm Reallocate


Thuật toán tái thiết lập tài nguyên [CT7], [CT8] thực hiện tác vụ được thể hiện chi tiết trong Algorithm 2.2 sau đây.


Algorithm 2.2. Reallocate

Input: currentBest (các thể tốt nhất sau mỗi thế hệ)

Output: lịch biểu sau khi được hiệu chỉnh

Có thể bạn quan tâm!

Xem toàn bộ 156 trang tài liệu này.


1. makespan = f(currentBest)

2. newbest = currentBest;

3. Lb = lastResource (newbest) //tài nguyên hoàn thành sau cùng

4. Wb = {các tác vụ được thực hiện bởi Lb}

5. For i=1 to size(Wb) // duyệt lần lượt từng tác vụ

6. Wi = Wb[i]; // lấy tác vụ thứ i

7. Li = {các tài nguyên thực hiện được Wi # Lb}

8. For j = 1 to size(Li) // duyệt lần lượt từng tài nguyên

9. Li[j] = Li[j] + {Wi} // chuyển ti sang Li[j]

10. Lb = Lb – {Wi} // loại Wi khỏi Lb

11. newmakespan = f(newbest) // tính toán lại makespan

12. If newmakespan < makespan

13. makespan = newmakespan

14. Return newbest; // dịch chuyển thành công, trả về kết quả và dừng hàm

15. End if

16. newbest = currentBest; // dịch chuyển không thành công, lấy lại lịch biểu ban đầu (trước khi dịch chuyển) để thực hiện vòng lặp tiếp theo

17. End for // j

18. End for // i

19. Return newbest;

End Function

Với:

- f: hàm tính makespan của một lịch biểu

- size: hàm tính số phần tử của một tập/mảng

- lastResource: hàm trả về tài nguyên kết thúc thực hiện sau cùng

Ví dụ 2.3:


Xem xét một dự án với các thông tin như sau:


- Tập tác vụ W ={1, 2, 3, 4, 5, 6, 7, 8, 9, 10}

- Tập tài nguyên L={1, 2, 3}.


Bắt đầu

newbest = Cbest; makespan = f(newbest)

WR

Lb = max(newbest); i=0

b = {các task trong Lb}

i++; i < size(WR )

Sai

b

Đúng

Wi ∈ WR , i=1.. size(WR ); j=0

b

b

Lt = {tập tài nguyên thực hiện được Wi } # Lb

F

j++; j < size(Lt)


T

Thêm Wi vào Ltj Xóa Wi khỏi Lb

f(newbest) < makespan

Sai

Đúng

Cbest = newbest makespan = f(newbest)

Kết thúc


Hình 2.7. Sơ đồ khối thực hiện di chuyển tác vụ sang tài nguyên khác


Thời gian thực hiện tác vụ được thể hiện trong bảng 2.14.


Bảng 2.14: Thời gian thực hiện các tác vụ


Tác vụ

1

2

3

4

5

6

7

8

9

10

Thời gian

2

4

3

5

2

2

5

3

4

2

Hình 2.8 thể hiện mối quan hệ giữa các tác vụ. Cụ thể như sau:


- Task 2 thực hiện và hoàn thành trước khi task 6,8 bắt đầu;

- Task 3 thực hiện và hoàn thành trước khi task 7 bắt đầu;

- Task 4 thực hiện và hoàn thành trước khi task 5 bắt đầu;

- Task 8 thực hiện và hoàn thành trước khi task 9 bắt đầu;

- Task 5 thực hiện và hoàn thành trước khi task 10 bắt đầu.


Task 0 và task 11 là 2 tác vụ giả với thời gian thực hiện bằng 0, thể hiện là thời điểm bắt đầu và kết thúc dự án.


W6

W2

W8

W9

W0

W1

W3

W7

W11

W4

W10

W5

Hình 2.8. Thứ tự ưu tiên của các tác vụ Năng lực của các tài nguyên được cho như trong bảng 2.15.

Bảng 2.15: Năng lực các tài nguyên


Tác vụ

W1

W2

W3

W4

W5

W6

W7

W8

W9

W10

L1

×

×

×

×



×


×

×

L2

×


×

×

×

×


×

×


L3

×


×


×


×

×


×

Giả sử, sau một thế hệ, ta tìm được lịch biểu với tài nguyên thực hiện tác vụ được thiết lập như trong bảng 2.16.


Bảng 2.16: Tài nguyên thực hiện tác vụ


Tác vụ

1

2

3

4

5

6

7

8

9

10

Tài nguyên

1

1

2

1

2

2

3

2

1

1

Ta có thể thấy, biểu đồ Gantt của lịch biểu 2.15 như trong hình 2.9 dưới đây. Makespan của lịch biểu 2.15 là: 17


L1

W1

W2

W4

W9

W10

L2

W3

W5

W6

W8


L3

W7


Time

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

16

17

Hình 2.9. Biểu đồ Gantt của lịch biểu 2.15

Áp dụng hàm Reallocate, ta thiết lập tài nguyên thực hiện tác vụ W9 là L2, lịch biểu mới được biểu diễn như trong hình 2.10. Lịch biểu mới có makespan là 16, tốt hơn so với kết quả trước.


L1

W1

W2

W4

W10


L2

W3

W5

W6

W8

W9


L3

W7


Time

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

16

17

Hình 2.10. Biểu đồ Gantt của lịch biểu mới

Cụ thể các việc tái thiết lập tài nguyên thực hiện tác vụ được thể hiện trong hình 2.11 dưới đây.


Resources

Before Reallocate


After Reallocate


Time


Hình 2.11. Minh họa phương pháp tái thiết lập tài nguyên

..... Xem trang tiếp theo?
⇦ Trang trước - Trang tiếp theo ⇨

Ngày đăng: 14/07/2022