Mạch điện - Trường CĐ Giao thông Vận tải - 11

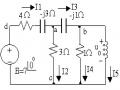
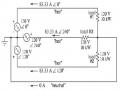
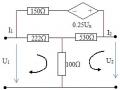
4.13. Cho mạch như hình vẽ . Tính dòng trên các pha nguồn và tải

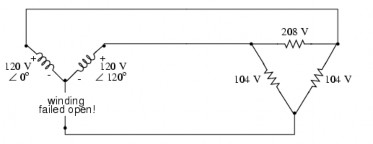
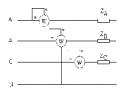
4.14. Cho mạch như hình vẽ. Tính dòng dây

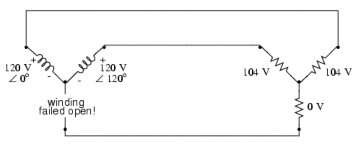
5.1. KHÁI NIỆM‌

CHƯƠNG V MẠNG HAI CỬA

‒ Là thiết bị điện có một cửa ngõ để nhận năng lượng hay tín hiệu, một cửa khác để trao đổi năng lượng hay tín hiệu với các bộ phận khác.

R, L

C, M

I1 I2

U1 U2

‒ Dòng vào cực 1 phải bằng dòng chảy ra trên cực kia.

‒ Mạng hai cửa có nguồn (tích cực), không nguồn (thụ động).

5.2. HỆ PHƯƠNG TRINH TRẠNG THÁI

5.2.1. Hệ phương trình trạng thái dạng Z (Tổng trở)

. . . .

‒ Biểu diễn ( U1 , U 2 ) theo ( I1 , I2 )

. . .

U1  Z11 I1  Z12 I2

. . .

U2  Z21 I1  Z22 I2

‒ Viết dưới dạng ma trận là :

. . 

U1  Z.I1 

. . 

‒ Ma trận tổng trở Z là :

U 2 I2 



Z Z11 Z12 

Z



21

Z22 

‒ Các thông số Zik không phụ thuộc vào dòng, áp mà chỉ phụ thuộc vào các phần tử ở bên trong trong mạng hai cửa : R, L, C.

Z11

: Trở kháng vào cửa 1 khi hở mạch cửa 2.

.

U1

.

I1

I2 0

Z12

Z21

: Trở kháng tương hỗ giữa cửa 1 đối với cửa 2 khi hở mạch cửa 1.

.

U1

.

I2

.

U 2

.

I1

I1 0

: Trở kháng tương hỗ giữa cửa 2 đối với cửa 1 khi hở mạch cửa 2.

I2 0

Z22

: Trở kháng vào cửa 2 khi hở mạch cửa 1.

.

U 2

.

I2

I1 0

‒ Đơn vị tính trở kháng trên là .

‒ Mạch tương đương :

‒ Cách xác định các thông số:

Cách 1 :

. .

‒ Dựa vào mạch điện cụ thể tìm ra cách viết quan hệ giữa các biến ( U1 , U 2 ) theo

. .

( I1 , I2 ) sao cho giống dạng hệ phương trình trạng thái các hệ số đứng trước I1, I2 sẽ chính là các thống số Zik cần tìm.

Cách 2 :

‒ Tính các thông số Zik theo công thức ngắn mạch hoặc hở mạch.

Ví dụ 1 :

U1

I

Z3

U2

1

I2

Cho mạng hai cửa. Xác định thông số Zik hoặc ma trận Z. Mạng hai cửa hình T :

. . .

Z1 Z2

U1  Z11 I1  Z12 I2

. . .

U2  Z21 I1  Z22 I2

Cách 1 : Áp dụng vòng mắc lưới :

. . .

 U1  (Z1  Z2 ) I1  Z2 I2

. . .

U2  Z2I1  (Z2 Z3) I2

Cách 2 :

Z11  Z1 Z2

Z  Z



12 2

Z21  Z2

22 2 2

Z  Z  Z

. . .

 U1  (Z1  Z2 ) I1  Z2 I2

. . .

Hở mạch cửa 2 : I2 = 0

.

U2  Z2I1  (Z2 Z3) I2

U1

I

Z3

U2

1

I2 = 0

Z1 Z2



U1

Z11 .

I1

.

 Ztđ1  Z1



.

 Z2



U2

Z21 .

I1

Z2 I1

.

I1

 Z2

Hở mạch cửa 1 : I1 = 0

.

Z1 Z2

U1

I

Z3

U2

1 = 0

I2



U2

Z22 .

I2

.

 Ztđ 2



.

 Z2  Z3



U1

Z12 .

I2

Z2 I2

.

I2

 Z2

Ví dụ 2 :

Cho mạng hai cửa. Xác định thông số zik hoặc ma trận Z.

Z1

Mạng hai cửa hình : Z1

I1

I2

U

Z3 Z4

1 U2

Cách 2 :

. . .

U1  Z11 I1  Z12 I2

. . .

U2  Z21 I1  Z22 I2

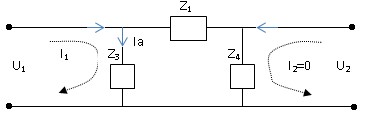
Hở mạch cửa 2 : I2 = 0

.

1

2

Z U1  Z

 (Z1  Z4 ).Z2

11 .

I1

tđ  Z

 Z4

.

Z U2

Z

.

.

 Ia Z4 

Z4 .Z2

21 .

I1

I1 Z1

 Z2  Z4

. .

Ia  I1

Z2

Z1  Z2  Z4

U1

I1 = 0

Z2

Ib

Z4

U2

Hở mạch cửa 1 : I1 = 0 Z1

.

1

2

Z U2  Z

I2

Z

 (Z1  Z2 ).Z4

22 .

I2

tđ  Z

 Z4

.

Z U1

.

.

 Ib Z2 

Z4 .Z2

12 .

I2

I2 Z1

.

 Z2  Z4

. Z4

Ib  I2

Z1  Z2  Z4

5.2.2. Hệ phương trình trạng thái dạng Y (Dẫn nạp)

. . . .

‒ Biểu diễn ( I1 , I2 ) theo ( U1 , U 2 )

. . .

I1  Y11 U1  Y12 U2

. . .

I2  Y21 U1  Y22 U2

‒ Viết dưới dạng ma trận là:

. . 

.

.

I1  Y.U1 

I2

‒ Hay tổng trở Z là :

Y Y11

U2

Y12 

Y Y 

21 22 

‒ Các thông số Zik không phụ thuộc vào dòng áp mà chỉ phụ thuộc vào các phần tử ở bên trong trong mạng hai cửa: R, L, C.

Y11

Y12

Y21

Y22

: Dẫn nạp vào cửa 1 khi ngắn mạch cửa 2.

.

I1

.

U1

.

I1

.

U 2

U2 0

: Dẫn nạp tương hỗ giữa cửa 1 đối với cửa 2 khi ngắn mạch cửa 1.

.

I2

.

U1

U1 0

: Dẫn nạp tương hỗ giữa cửa 2 đối với cửa 1 khi ngắn mạch cửa 2.

.

I2

.

U 2

U2 0

: Dẫn nạp vào cửa 2 khi ngắn mạch cửa 1.

U1 0

Z1

U

Z2

Z3

1

U2

Cách 1 : Áp dụng thế nút

I1

I2

. 1 1 . 1 .

I1  ( Z

 ) U1  (

Z Z

) U2

1

. 1



I2 (

Z2

2

1

.

) U1  (

Z1

1

1

.

 ) U2

Z3

‒ Suy ra giá trị cần tìm:

Y  ( 1 1 ) Y  ( 1 1 )

11



Z1 Z2

22



Z1 Z3

Y ( 1 ) Y ( 1 )

2

2

12 Z21 Z

Cách 2 : Ngắn mạch từng cửa

‒ Ngắn mạch cửa 1: U1 = 0

.

Y I2 1

 (Z1

Z

1

 Z3 )

22 .

U2

.



I1

Y12 .

U 2

Ztđ

.



I1

.

Z1 I1

Z1Z3

1

Z1

Z2 Z3

I1

I2

U1 = 0 U2

‒ Ngắn mạch cửa 2: U2 = 0

.

Y I1 1

 (Z1

Z

1

 Z2 )

11 .

U1

.

Ztđ



.

I1

Z1Z2

U

Z2

1

Z3

I2

U2 = 0



I2

Y21 .

U1

I2

.

Z3 I2

1

Z3

5.2.3. Hệ phương trình trạng thái dạng H (Hệ số khuếch đại)

. . . .

‒ Biểu diễn ( U1 , I2 ) theo ( I1 , U 2 )

. . .

U1  H11 I1  H12 U2

. . .

I2  H21 I1  H22 U2

‒ Các thông số Hik không phụ thuộc vào dòng áp mà chỉ phụ thuộc vào các phần tử ở bên trong trong mạng hai cửa: R, L, C.

H11

H12

H 21

H 22

: Trở kháng vào vào cửa 1 khi ngắn mạch cửa 2.

.

U1

.

I1

.

U1

.

U 2

U2 0

: Hàm truyền đạt áp ( hệ số khuyếch đạt) khi hở mạch cửa 1.

.

I2

.

I1

I1 0

: Hàm truyền đạt dòng khi ngắn mạch cửa 2.

.

I2

.

U 2

U2 0

: Dẫn nạp vào cửa 2 khi hở mạch cửa 1.

I1 0

5.2.4. Hệ phương trình trạng thái dạng G

. . . .

‒ Biểu diễn ( I1 , U 2 ) theo ( U1 , I2 )

. . .

I1  G11 U1  G12 I2

. . .

U2  G21 U1  G22 I2

5.2.5. Hệ phương trình trạng thái dạng A

. . . .

Biểu diễn ( U1 , I1 ) theo ( U 2 ,I2 )

. . .

U1  A11 U2  A12 I2

. . .

I1  A21 U2  A22 I2

5.2.6. Hệ phương trình trạng thái dạng B

. . . .

. . .

Biểu diễn ( U , I ) theo ( U ,I ) :

U2  B11 U1  B12 I1

2 2 1 1

. . .

I2  B21 U1  B22 I1

Ví dụ 1 : (SV tự giải)

Cho mạch điện. Tính thông số Z, H.

2

4

4

U1

4

U2

Ví dụ 2 : (SV tự giải)

Cho mạch điện. Tính thông số Z, H.

4 4

U1

4

U2

5.3. PHÂN LOẠI MẠNG HAI CỬA

5.3.1. Mạng hai cửa tương hỗ

Ma Trận

Z	Y	H	G	A	B
Điều kiện tương hỗ	Z12 = Z12	Y12 = Y12	H12 = -H12	G12 = -G12	A =-1	B =1

Có thể bạn quan tâm!

• Định Lý Thevenin Và Định Lý Norton:
• Hệ Thống Đối Xứng Bốn Dây Và Cách Giải
• Các Đại Lượng Công Suất Khác Và Hiệu Chỉnh Hệ Số Công Suất
• Mạch điện - Trường CĐ Giao thông Vận tải - 12

Xem toàn bộ 99 trang tài liệu này.

A = A11 A22 - A12A21 = -1

‒ Mạch có tính chất tương hỗ có ba thống số độc lập.

5.3.2. Mạng hai cửa đối xứng

‒ Khi thay đổi chiều truyền đạt cửa 1và cửa 2 thì tính chất và các phương trình không thay đổi.

Ma Trận

Z	Y	H	G	A	B
Điều kiện đối xứng	Z11 = Z22	Y11 = Y22	H = 1	G = 1	A11 = A22	B11 = B22

‒ Một mạng hai cửa đối xứng thì tương hỗ và có hai thông số độc lập.