((
gWorker = i;
EndIf Else
Có thể bạn quan tâm!
-
Lập Lịch Round Robin Dựa Trên Sự Ưu Tiên Về Khả Năng Tính Toán -
Giản Đồ Lập Lịch Round Robin Dựa Trên Kiểm Thử Độ Tin Cậy -
Giải pháp nâng cao hiệu quả của giản đồ lập lịch dựa trên độ tin cậy trong các hệ thống tính toán tình nguyện - 8 -
Giải pháp nâng cao hiệu quả của giản đồ lập lịch dựa trên độ tin cậy trong các hệ thống tính toán tình nguyện - 10
Xem toàn bộ 83 trang tài liệu này.
//Ưu tiên theo khả năng tính toán If 
Endif EndFor
EndIf EndIf
Endif
gWorker = i;
If (Tồn tại bWorker)
return bWorker;
EndIf
If (Tồn tại gWorker)
return gWorker;
EndIf
Return NULL;
Tiếp theo tôi sẽ xác định lại tính khả dụng của các giản đồ lập lịch dựa trên độ tin cậy bằng các kết quả mô phỏng trong phần 5.
Chương 4. KẾT QUẢ THỰC NGHIỆM
Trong phần này sẽ giới thiệu về chương trình mô phỏng, kịch bản mô phỏng và thảo luận về các kết quả mô phỏng.
4.1 Chương trình mô phỏng
Trong phần này, tôi xin trình bày về chương trình mô phỏng được dùng trong luận văn của tôi, chương trình mô phỏng VCSIM. VCSIM được xây dựng trên mô hình hướng sự kiện. Đây là mô hình sử dụng trong BOINC. VCSIM mô phỏng việc tạo và phân bố các nhiệm vụ được thực thi trong môi trường có sự thay đổi cao, không đồng nhất và phân tán. Thêm vào đó nó còn tập hợp và đánh giá hiệu quả của các nhiệm vụ hoàn thành. VCSIM được viết bằng ngôn ngữ lập trình C.
VCSIM được thiết kế gồm các mô đun chính là: Mô đun quản lý máy trạm, mô đun quản lý công việc, mô đun mô phỏng. Mô đun quản lý máy trạm thực hiện nhiệm vụ tạo ra danh sách các máy trạm có độ tin cậy ban đầu giống giau, có thời gian tính toán khác nhau, tạo ra các máy giả mạo, quản lý các máy trạm như lấy máy trạm từ hàng đợi theo các tiêu chí lập lịch, đẩy máy trạm vào hàng đợi …Mô đun quản lý công việc thực hiện nhiệm vụ tạo ra danh sách các nhiệm vụ, gán nhiệm vụ cho các máy trạm, quản lý hàng đợi công việc, tính độ tin cậy của các nhiệm vụ…Mô đun mô phỏng thực hiện nhiệm vụ quản lý danh sách các tham số mô phỏng như số lần mô phỏng, số máy trạm thực hiện, số công việc được thực hiện, phân số lỗi, tỉ lệ lỗi chấp nhận được, số lần thực hiện lại của các nhiệm vụ, tỉ lệ phá hoại, giản đồ lập lịch thực hiện, tỉ lệ kiểm tra điểm, tham số hỗ trợ danh sách đen hay không, tham số hỗ trợ kiểm tra điểm theo biểu quyết hay không …. Thực hiện mô phỏng, hỗ trợ các hàm hiển thị và đưa ra kết quả.
4.2 Kịch bản mô phỏng
Trong phần này, tôi xác định hiêu quả của giản đồ lập lịch được đề xuất bởi các mô phỏng. Trong mô phỏng của tôi, một tính toán chứa đựng một danh sách của N các
nhiệm vụ độc lập có kích cỡ giống nhau và một danh sách P các máy tính tình nguyện (các máy trạm). Để mô phỏng sự phá hoại của các máy xấu, một phân số f =
0.2 của các máy trạm được lựa chọn ngẫu nhiên là phá hoại. Có hai trường hợp về số lượng nhiệm vụ và máy trạm được quan tâm.
Trong trường hợp thứ nhất (N > P), có 1500 nhiệm vụ và 500 máy trạm, trong trường hợp thừ hai (N < P ), có 500 và 1500 máy trạm. Giả sử rằng chính sách danh sách đen không được áp dụng (ví dụ. máy trạm có thể đệ trình kết quả thậm chí sau khi nó được dò tìm là một kẻ phá hoại), kĩ thuật kiểm tra điểm dựa trên biểu quyết được sử dụng trong quá trình mô phỏng. Bởi vì hiệu năng của giản đồ lập lịch dựa trên độ tin cậy được đánh giá theo tham số sự chậm chễ (ví dụ. tỉ số giữa thời gian chạy của quá trình tính toán với hoặc không dùng kĩ thuật chịu đựng lỗi), tôi có thể giả sử rằng thời gian thực thi của một nhiệm vụ trên một máy trạm là một số ngẫu nhiên giữa 1 đến 5 đơn vị thời gian. Mục đích chính của mô phỏng này là so sánh hiệu năng của các giản đồ lập lịch: Round Robin RR, lập lịch Round Robin dựa trên sự ưu tiên về khả năng thực hiện PRR(Av), lập lịch Round Robin dựa trên sự ưu tiên độ tin cậy PRR(Cr), Lập lịch Round Robin dựa trên kiểm thử tin cậy với tiêu chí ưu tiên độ tin cậy CRR(Cr) và ưu tiên khả năng thực hiện CRR(Av). Để đảm bảo độ tin cậy của kết quả mô phỏng tôi sẽ thực hiện mô phỏng mỗi trường hợp 5 lần và lấy giá trị trung bình.
4.3 Kết quả
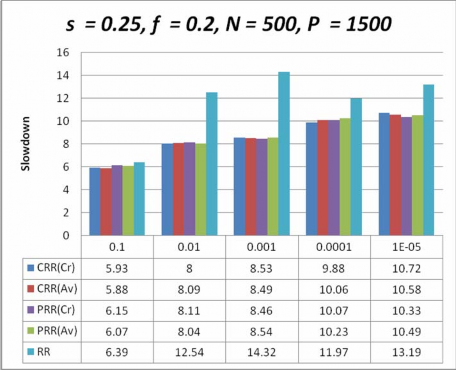
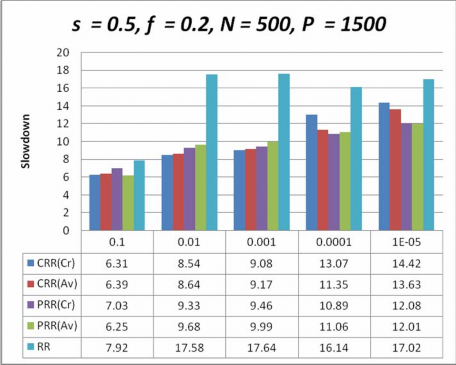
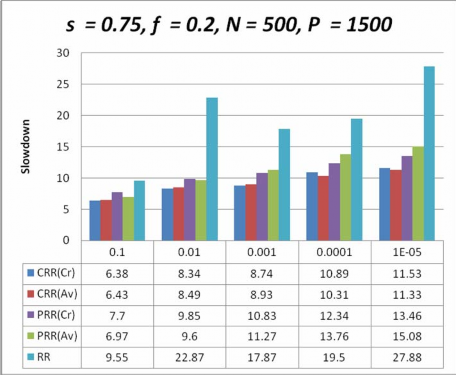
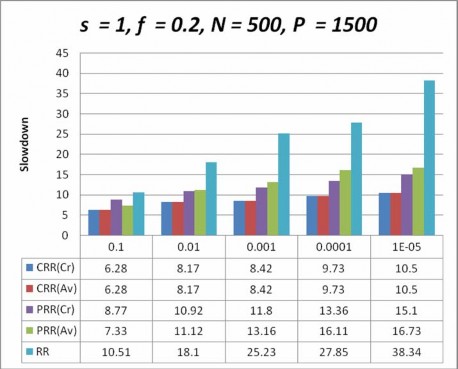
Hình 4-1, 4-2, 4-3, 4-4, chỉ định các kết quả thí nghiệm ứng với các trường hợp tỉ lệ lỗi khác nhau khi số lượng công việc lớn hơn số máy và Hình 4-5, 4-6, 4-7, 4-8 chỉ định các kết quả thí nghiệm ứng với các trường hợp tỉ lệ lỗi khác nhau khi số lượng công việc nhỏ hơn số máy trạm, lấy được từ mô phỏng cho đồng thời các giản đồ lập lịch, tôi vẽ biểu đồ giá trị của tham số sự chậm chễ (slowdown) so với các tham số khác bởi vì nó là một tham số hiệu năng quan trọng khi chấp nhận một giản đồ chịu lỗi dựa trên độ tin cậy trong hệ thống tính toán tình nguyện.
Nhìn vào các kết quả của biều đồ so sánh tôi nhận thấy rằng các giản đồ lập lịch do tôi đề xuất đều giảm đáng kể thời gian thực thi so với giản đồ lập lịch Round Robin
tương ứng. Đặc biệt trong trường hợp trong cả hai trường hợp N > P hay N < P thì giản đồ lập lịch CRR giảm từ 40% - 60% so với giản đồ lập lịch RR tương tứng. Còn trong trường hợp trong cả hai trường hợp N > P hay N < P thì
giản đồ lập lịch CRR giảm xấp xỉ 60% - 80% so với giản đồ lập lịch RR tương tứng. Trong trường hợp N > P, N < P thì giản giản đồ lập lịch CRR hiệu quả hơn PRR(Cr) và PRR(Av) ngoại trừ trường hợp N < P và và tỉ lệ lỗi của kết quả
nhỏ hơn 0.001 . Còn giản đồ lập lịch PRR(Cr) thì hiệu quả hơn một chút so với PRR(Av) khi tỉ lệ lỗi nhỏ hơn 0.001. Còn lai là gần như tương đương nhau.
Sở dĩ các giản đồ có các kết quả tốt như trên là do các giản đồ đã quan tâm đến việc chọn các máy trạm sao cho nâng cao được độ tin cậy của nhiệm vụ sau mỗi lần tính toán của máy trạm để cho độ tin cậy của nhiệm vụ nhanh hướng được tới ngưỡng tin cậy.
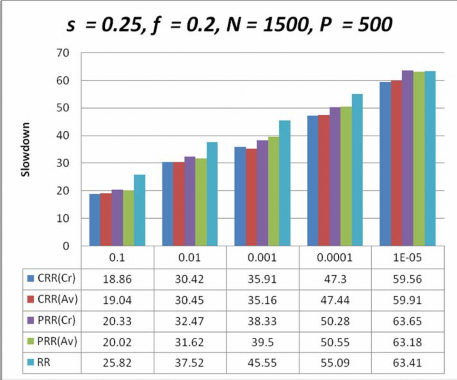
Hình 4-1. Biểu đồ so sánh sự chậm chễ của các giản đồ lập lịch với s= 0.25,N >P
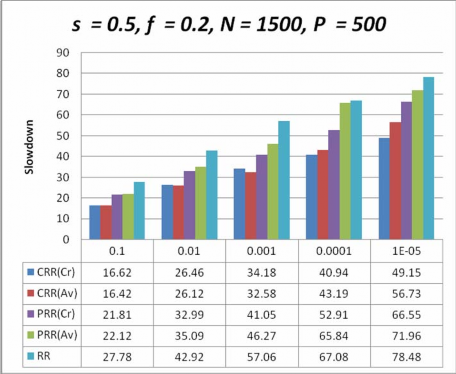
Hình 4-2. Biểu đồ so sánh sự chậm chễ của các giản đồ lập lịch với s= 0.5,N >P
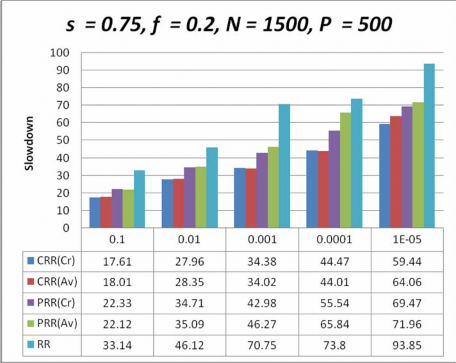
Hình 4-3 Biểu đồ so sánh sự chậm chễ của các giản đồ lập lịch với s= 0.75,N >P
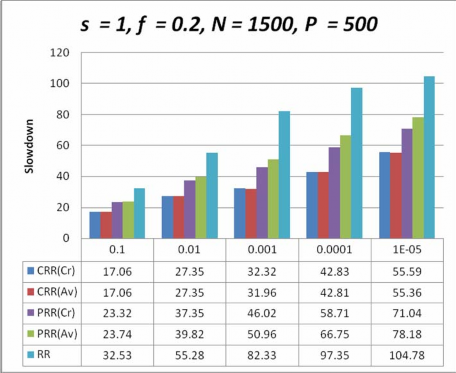
Hình 4-4. Biểu đồ so sánh sự chậm chễ của các giản đồ lập lịch với s= 1,N >P
Hình 4-5. Biểu đồ so sánh sự chậm chễ của các giản đồ lập lịch với s= 0.25,N< P
Hình 4-6. Biểu đồ so sánh sự chậm chễ của các giản đồ lập lịch với s= 0.5,N< P
Hình 4-7. Biểu đồ so sánh sự chậm chễ của các giản đồ lập lịch với s= 0.75,N< P
Hình 4-8. Biểu đồ so sánh sự chậm chễ của các giản đồ lập lịch với s= 1,N< P