Thu Gọn Hệ Lực Quán Tính Của Vật Rắn

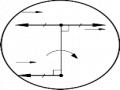
Vậy :

S x1 = F1 y1 =20.5=100 cm3 S y1 = F1 x1 = 20.1=20 cm3

y

2 cm

4/3 cm

2cm

S x 2 =F 2 y 2 =4.1= 4 cm3 Sy2 = F 2 x2 = 4.3 = 12 cm3

10 cm

C

Có thể bạn quan tâm!

• Các Yếu Tố Động Học Của Chuyển Động Của Hình Phẳng
• Các Định Luật Cơ Bản Của Động Lực Học Và Phương Trình Vi Phân Chuyển Động Của Chất Điểm
• Nguyên Lý Đalămbe Đối Với Chất Điểm :
• Tính Công Suất Của Chuyển Động Thẳng Và Chuyển Động Quay.
• Định Lý Biến Thiên Động Lượng Của Hệ Chất Điểm.
• Cơ lý thuyết Nghề Cắt gọt kim loại - Cao đẳng nghề Phần 2 - Tổng cục Dạy nghề - 9

Xem toàn bộ 83 trang tài liệu này.

x = S y1 S y 2 = 20 12= 32 = 4 cm

F1 F2 20  4 24 3

C

y = S x1 S x 2 = 100  4 = 104 =4,3 cm

4,3 cm

F1 F2 20  4 24

2 cm

x

Hình13-5

Ví dụ 2 : Tìm khối tâm (trọng tâm) của tấm tròn đồng chất tâm O, bán kính R, bị khuyết mảnh tròn tâm A, bán kính r. Biết OA= a, a+ r < R (hình 13-6 )

Bài làm :

2

2

Xem tấm bị khuyết là kết quả của việc ghép tấm tròn nguyên có khối tâm (trọng tâm) tại O (0;0), diện tích F1 = r với mảnh tròn có khối tâm (trọng tâm) là A (0,0) ,diện tích âm F 2 = - r .

y

r

C

O

A

x

Do tấm có trục O x đối xứng nên khối tâm (trọng tâm) nằm trên trục này (Y C =O), còn

S y1 S y 2

F

X C =

1

F Y

F2

F Y

.R 2 .O .r 2 .a

X =

C

1 1 2 2= 2 2

F1 F2

.R

.r

a.r 2

X C = - R 2

r 2

Dấu (-) chứng tỏ C nằm bên trái tâm O.

Hình13-6

2.1.3. Mômen quán tính của vật rắn

- Mô men quán tính của vật rắn đối với trục z (hình 13-7)

Zk

k mk

rk

yk

Xk

x

y

Hình13-7

Kí hiệu: J z là đại lượng vô z

- Mô men quán tính của vật rắn đối với các trục toạ độ:

Kí hiệu: Jx ; Jy ; J z

- Mô men quán tính ly tâm là các đại lượng sau:

Kí hiệu: Jxy ; Jxz ; Jyz Trục quán tính chính:

- Trục x được gọi là trục quán tính chính nếu J xy = J xz = O

- Trục y được gọi là trục quán tính chính nếu J yx =J yz = O

- Trục z là trục quán tính chính khi J zx = J zy = O

Mô men quán tính của vật rắn đối với 1 điểm. Kí hiệu: JO

Bán kính quán tính :

2 J z

=

qt M

Đại lượng

2 J z được gọi là bán kính quán tính của vật rắn đối với trục z.

=

qt M



C

d

C

Đơn vị của mô men quán tính là kgm 2 , đơn vị của bán kính quán tính là m Mô men quán tính độc cực: J O = J x + J y

- Mô men quán tính của vật rắn đối với trục

bằng tổng mô men quán tính của nó đối với trục song song với trục qua khối tâm C của vật và tích của khối lượng vật với bình phương khoảng cách giữa hai trục (hình 13-8):

C

J = J + Md 2

Hệ trục quán tính chính:

- Nếu vật rắn đồng chất có một mặt phẳng đối xứng thì trục thẳng góc với

Hình 13-8

mặt phẳng đối xứng là trục quán tính chính tại giao điểm của mặt phẳng đối xứng và trục (hình 13-9).

- Nếu vật rắn đồng chất có một trục đối xứng thì trục đó là trục quán tính chính trung tâm (hình 13-10).

c

c



C

C

Hình13-9 Hình 13-10

Mô men quán tính của một số vật đồng chất:

- Thanh đồng chất có chiều dài L, khối lượng m (hình 13-11):

J C =

mL2

12

; J x

= J z =

mL2

3

; J y

= O (13-7)

- Vành tròn đồng chất có bán kính R, khối lượng m (hình 13-12):

x

y

J = mR 2 ; J

= J z =

mR2

2

(13-8)

C

A

B

L/2

C

y

x

L

R

C

y

z z

Hình13-11 Hình13-12

- Mặt tròn đồng chất. Bán kính R, khối lượng m (hình 13-13):

J x =

mR2

2

; J y

= J z

= mR

2

4

(13- 9)

C

z y

x

x

Hình13-13 Hình 13-14

- Tấm chữ nhật đồng chất, có các cạnh 2a, 2b, khối lượng m (hình 13-14):

J x =

mb2

12

; J y =

ma2

12

(13-10)

- Trụ tròn xoay đồng chất, có khối lượng m, bán kính R, chiều cao h

+ Trụ rỗng (hình 13-15):

z

x

J = mR 2 ; J

= J y =

m ( R 2 + h

2

2 6

) (13-11)

+ Trụ đặc (hình 13-16):

J z =

mR2

2

; J x

= J y =

m ( R 2 + h

2

4 3

) (13-12)

h

y

C

h

y

x

z z

x

Hình13-15 Hình13-16

Các kết quả trên có thể áp dụng trực tiếp cho trường hợp của tiết diện phẳng có tiết diện F, ví dụ tương ứng với công thức (13-8), (13-9), (13-10) ta có:

- Vành tròn đồng chất :

x

y

J = FR 2 = R 4 ; J

= J z =

FR 2

2

= R 4

2

(13-13)

- Mặt tròn đồng chất :

J x =

R 4

2

; J y

= J z

= R 4

4

(13-14)

- Tấm chữ nhật đồng chất :

J x =

ab3

12

; J y

= ba3

12

(13-15)

2.2. Vật chuyển động tịnh tiến.

Với vật rắn có chuyển động bất kỳ, véctơ chính của hệ lực quán tính của nó luôn luôn bằng

C

Rqt M .a

Trong đó: M là khối lượng của vật

aC là gia tốc của khối tâm của vật rắn

Mômen chính của hệ lực quán tính của vật rắn chuyển động phụ thuộc vào dạng chuyển động cụ thể của vật rắn.

C

k

k

k

k

k

k

Vật rắn chuyển động tịnh tiến: Mômen chính của hệ lực quán tính đối với khối tâm vật rắn được tính như sau:

C

mqt

m

F qt r

F qt

r

m .a

(13-16)

Trong đó: rk là véc tơ định vị của chất điểm Mk đối với khối tâm C, tức là:

rk CMk ;

rC  0

Fqt

Mk(mk )

Chú ý:

k

akaC; mkrkM rC 0

rkWC

F

qt

qt

k mk ak

maC

qt C Wk

F

Vậy :

k mk wk

Hình 13-17

C

k

mqt r

m a

a

m r

a

m r a

m r a

M r  0

k

k

k

k

k

C

k

k

C

k

k

C

C

Do đó thu gọn hệ lực quán tính của vật chuyển động tịnh tiến về khối tâm C ta được một lực đặt tại khối tâm C.

Rqt

M aC

2.3. Vật quay quanh trục cố định.

2.3.1. Thu gọn hệ lực quán tính của vật rắn

Vật quay quanh một trục cố định với vận tốc góc và gia tốc góc là 

(Hình 13-18)

Chọn hệ trục tọa độ Oxyz gắn liền vào vật quay, trong đó Oz trùng với trục quay của vật. Lấy phần tử Mk có khối lượng mk và véc tơ định vị rkxk,yk,zk. Gia tốc của điểm Mk bằng:

k

k

a at

a

n

kk rk

vk ;

z

vk rk B

Lực quán tính của chất điểm Mk sẽ là: ω

k

k

k

k

k

F qt m r m v 

Vậy mômen chính của hệ lực quán tính của vật rắn đối với gốc tọa độ O sẽ bằng:

ε an

at

Mk

mqt m F qt 

qt

F

kHình 13-1

qtn

F

rk k

O O k

O

mqt r

m r r

m v O

k

k

k

k

k

k

y

Trong hệ trục tọa độ đã chọn, các véc tơ xA

k

r ;;được xác định theo các véctơ đơn vị



trên các trục tọa độ như sau:

Hình 13-18

i , j, k

r x iy

j 





; ; 

k k k

zk k k k

Sau khi thực hiện các phép tính chú ý :

ij 



k ; j k i ;k 



xy

xz

z k

Ta được :

j i ;i i j j k k  0

m

qt O

Trong đó :

2 J

J zx

i2 J

J zy

j J 

(13-17)

xz

k

k

k

J m x z ; J

m y z ; J

m

(x2 y2 )

(13-18)

yz

k

k

k

z

k

k

k

Véc tơ chính của hệ lực quán tính ,như trên đã nêu, bằng

C

Rqt ' M a M r r 

C C

Sau khi thay :

rC xC

iy



z

C

C

C

C

j 

C

C k

Ta có:

Rqt ' M x

2 y

iM y

2 x

j

(13-19)

Như vậy thu gọn hệ lực quán tính của vật quay quanh một trục cố định về một điểm nằm trên trục quay của vật ta được một lực tính theo công thức (13-17) và một ngẫu lực tính theo công thức (13-19)

2.3.2. Phương trình xác định phản lực trục quay

z

B

RBx

RBy

F1

F2

O

C

F3

FN

RA

RAy y

C

y

RAx

xC

x

Khảo sát vật rắn chuyển động quay quanh một trục cố định dưới tác dụng của các lực hoạt

động F1, F2,....,FNcó vận tốc góc và gia tốc

góc .

Các ngoại lực tác dụng lên vật rắn bao

gồm các lực hoạt động

F1, F2....,FN và các

phản lực tại ổ trục

RA và RB

Chọn hệ trục tọa độ Axyz gắn liền vào vật, có trục Az trùng với trục quay. (Hình13-19)

m

Hệ lực quán tính của vật rắn thu gọn về

R

A

tâm A được qt

và ngẫu lực qt

được tính theo

A

công thức (13-17) và (13-19)



Dựa trên phương pháp Tĩnh - Động lực hình học, ta viết các phương trình tĩnh học cho hệ lực

F , F ,...., F

, R

A

, R

,Rqt ,mqt

ta nhận được:

Hình 13-19

1

2

N

A

B

A

A

Fkx

ky

F

RAx

Ay

R

RBx

By

R

MyC

C

Mx 

MxC

C

My

2  0

2  0

yz

Fkz RAz  0

xz

mx

Fkmx

RA

mx

RB

J 2 J

zx 0

my

Fkmy

RA

my

RB

J 2 J

yz 0

mzFkJ z 0

Vì hệ trục tọa độ gắn liền vào vật quay nên các đại lượng xC, yC, zC, Jzx, Jz là không đổi

Như vậy ta nhận được sáu phương trình, trong đó phương trình cuối cùng không chứa các phản lực ổ trục, cho phép xác định chuyển động của vật quay, được gọi là phương trình vi phân vật quay quanh một trục cố định.

Năm phương trình còn lại cho phép ta xác định các phản lực ở ổ trục tại A

và B.

Chú ý rằng các phản lực ở ổ trục phụ thuộc vào các lực hoạt động và các

yếu tố động học của vật rắn, tức vận tốc góc ω và gia tốc góc ε.

Thành phần của phản lực ổ trục chỉ phụ thuộc vào các yếu tố động học của vật quay (ω, ε) gọi là phản lực động lực của ổ trục.

Phản lực ở ổ trục được biểu diễn dưới dạng :

A

A

R Rt

A

Rđ;

R Rt

Rđ

B

B

B

Trong đó : -

t , Rt

là các thành phần không phụ thuộc vào chuyển động, tức

R

B

A

không chứa và được gọi là phản lực tĩnh

R

R

-

,

A B

đ đ là các thành phần phụ thuộc vào chuyển động, tức có chứa

và được gọi là phản lực động lực

Các thành phần phản lực động được xác định nhờ hệ phương trình sau:

R

R

đ đ

Ax Bx

MxC

2 My  0

C

Rđ Rđ My 2 Myx 0

Ay By C

x A x B yz xz

m Rđm

RdJ

2 J

 0

m Rđm RdJ 2J  0

y A y B xz yz

Các phương trình này được gọi là các phương trình xác định phản lực động lực. Việc xuất hiện các phản lực động lực làm giảm độ bền, độ chính xác,

năng suất và gây hư hỏng máy. Chính vì vậy cần phải triệt tiêu hoặc làm giảm các phản lực động lực. Điều kiện cần và đủ để triệt tiêu các phản lực động lực là trục quay phải thỏa mãn các điều kiện sau:

xC = yC = 0

Jxy = Jzx = 0

Tức là trục quay phải qua trọng tâm của vật rắn và là trục quán tính chính. Nói cách khác để triệt tiêu hoàn toàn phản lực động lực, trục quay phải là trục quán tính chính trung tâm.

Trong trường hợp trục quay không phải là trục quán tính chính trung tâm thì bằng cách thêm hoặc bớt khối lượng của vật quay, nó có thể trở thành trục quán tính chính trung tâm.