Quy Tắc Học Tích Cực Là Truy Vấn Các Nhãn Cho Các Điểm X Trong L, L Được Xác

Trong thuật toán perceptron chuẩn hình 3.1, bước cập nhật perceptron chuẩn vt+1 = vt + xt.yt là cùng hướng nhưng khác độ lớn (được chia theo hệ số 2|vt.xt|)

Các thuật toán Perceptron cải tiến chuẩn được đưa ra trong hình 3.2. Ta có

||vt||=1 (3.3)

Và "rt+1"2 ="rt"2 + 4(rt. xt)2"xt"2 — 4(rt. xt)2 = 1. (3.4) Ngược lại, đối với bản cải tiến Perceptron chuẩn, mức độ của vt tăng đều đặn. Với bản cải tiến đã sửa, lỗi có thể chỉ giảm bởi vì vt.u cũng chỉ giảm.

rt+1 + u = rt. u — 2(rt. xt). (xt. u) = rt. u + 2|rt. xt||xt. u|. (3.5)

Biểu thức thứ 3.4 xảy ra theo thực tế là vt phân lớp nhầm xt. Do vậy vt.u tăng, và sự tăng có thể bị chặn từ dưới bằng cách chỉ ra |rt. xt||xt. u| là lớn.

Trước đây Hamson và Kibler đã từng sử dụng bản cập nhật này cho việc học bộ phân tách tuyến tính [34], gọi là “Reflection” (Sự phản ánh), dựa trên phương pháp “Reflexion” của Motzkin and Schoenberg [40].

Có thể bạn quan tâm!

Xem toàn bộ 65 trang tài liệu này.

xt. rt+1 = xt. rt — 2(xt. rt)(xt. xt) = —(xt. rt) (3.6)

Nói chung, biểu thức (3.6) có thể coi là bản cập nhật sửa của dạng rt+1 = rt— α(rt. xt)xt, dạng này tương đương với phương pháp “Reflexion” trong việc giải bất đẳng thức tuyến tính [30][40]. Khi 2, vector vt không còn giữ độ dài cố định nữa, tuy nhiên cũng có thể xác minh được rằng các vector đơn vị tương ứng r^tthỏa mãn:

r^t+1. u = (r^t. u + α|r^t. xt||xt. u|)/ƒ1 — α(2 — α)(r^t. xt)2, (3.7)

Và do vậy bất kỳ sự lựa chọn nào [0,2] cũng đảm bảo rằng lỗi không tăng. Blum và cộng sự[4] đã sử dụng =1 bảo đảm rằng sự phát triển trong mẫu số (phân tích của họ đã không dựa vào tiến bộ trong tử số) miễn là r^t. u và

(r^t. xt)2bị chặn ở 0. Phương pháp tiếp cận của họ được sửa dụng một loạt như là một phần của thuật toán phức tạp hơn cho học noise_tolerant. Trong khung làm việc tuần tự, có thể chặn |r^t. xt||xt. u| bởi 0, dưới sự phân tán thống nhất, và do đó sự lựa chọn =2 là thuận lợi nhất, nhưng =1 sẽ có thể tốt hơn.

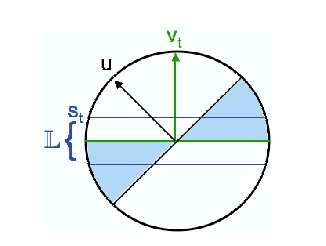
Hình 3.3 Quy tắc học tích cực là truy vấn các nhãn cho các điểm x trong L, L được xác định bởi ngưỡng st trên |vt.xt| [32]

3.1.4 Perceptron chỉnh sửa tích cực‌

Mục đích trong việc thiết kế luật học tích cực là giảm thiểu phức tạp nhãn được đưa vào câu truy vấn chỉ cho các nhãn trên các điểm trong miền lỗi

t. Tuy nhiên không có tri thức của u, thuật toán sẽ không biết vị trí của t. Theo trực giác thì luật học tích cực là xấp xỉ với miền lỗi, với thông tin đã cho thuật toán có vt. Trong hình 3.3, vùng đã gán nhãn L đơn giản là miền được hình thành bởi việc tạo ngưỡng cho các lề của một ví dụ ứng viên đối với vt.

Phiên bản tích cực của thuật toán Perceptron cải tiến được chỉ ra trong hình 3.4. Thuật toán này tương tự thuật toán của phần trước trong các bước cập nhật. Đối với quy tắc lọc, sẽ duy trì một ngưỡng st và chỉ yêu cầu cho các nhãn của các ví dụ có |rt. x| ≤ st. Miền xấp xỉ lỗi đạt được bằng cách chọn ngưỡng st thích hợp, để quản lý sự cân bằng giữa vùng L đang quá lớn, gây ra nhiều nhãn bị lãng phí mà không tìm được t, và L chỉ chứa các điểm có lề rất

nhỏ đối với vt, vì bước cập nhật sẽ tạo ra sự cải tiến rất nhỏ trên các điểm như thế. Thuật toán giảm ngưỡng thích ứng với thời gian, bắt đầu với s1=1/√d và giảm ngưỡng đi 2 lần cho đến khi nào có thể thực hiện các ví dụ đã gán nhãn trên ngưỡng là đúng.

Chúng ta giới hạn cận dưởi của st đối với lỗi chỉ ra rằng với xác suất cao thì ngưỡng st không bao giờ là nhỏ.

Perceptron cải tiến

chiều d, số lượng nhãn L và R

r1 = x1. y1 cho dữ liệu đầu tiên (x1, y1) s1 = 1/√d

For t=1 to L:

Chờ dữ liệu tiếp theo x: |x. rt| ≤ st và truy vấn nhãn của x. Gọi dữ liệu đã gán nhãn (xt, yt)

If(xt. rt)yt € 0, then:

rt+1 = rt — 2(rt. xt)xt st+1 = st

else

rt+1 = rt

If các dự đoán là đúng trên R dữ liệu đã gán nhãn liên tiếp (vd: (xi. ri) ≤ 0 6i C {t — R + 1, t — R, … , t}),

then st+1 = st/2 else st+1 = st

Hình 3.4. Một phiên bản tích cực của Perceptron đã chỉnh sửa. [32]

Thuật toán trong hình 3.4 đã được Dasgupta đã trình bày bằng cách cải tiến bước cập nhật của thuật toán perceptron [32], thu được một thuật toán đơn giản hơn, đạt được lỗi mục tiêu  bằng cách sử dụng số lượng nhãn xác

định 0˜(d log 1).

Trong lý thuyết phát triển của học tập tích cực, các kịch bản không tầm thường và cụ thể nhất mà trong đó học tập tích cực đã được thể hiện để cung cấp cho một sự cải tiến hàm số mũ trong độ phức tạp mẫu là học một một bộ phân tách tuyến tính cho các dữ liệu phân bố đều trên mặt cầu đơn vị.

3.2 Học tích cực với SVM‌

3.2.1 Giới thiệu‌

Bộ phân loại SVM đã được sử dụng rộng rãi trong rất nhiều bài toán phân lớp. Tuy nhiên chúng chỉ được sử dụng với tập dữ liệu huấn luyện đã được lựa chọn ngẫu nhiên. Trong mục này sẽ trình bày thuật toán Active Support Vector Machines (Acitve SVM) có thể làm giảm đi dung lượng cũng như sự cần thiết của tập dữ liệu huấn luyện.

3.2.2 Máy hỗ trợ vector‌

3.2.2.1 Máy vector hỗ trợ sử dụng phương pháp qui nạp

Máy vector hỗ trợ [41] có các cơ sở lý thuyết vững chắc và đạt được những thành công thực nghiệm xuất sắc. Chúng cũng được áp dụng cho những bài toán như: nhận dạng số viết bằng tay [24], nhận dạng đối tượng [13], và phân lớp văn bản [37][33].

Hãy xét thuật toán SVM cho bài toán phân lớp nhị phân. Cho tập huấn luyện {x1, x2, … , xn} là các vector trong không gian XRd và tập các nhãn

{y1, y2, … , yn} với yi {-1,1}. Theo cách hiểu thông thường nhất, thì SVMs là

các siêu phẳng chia tập dữ liệu huấn luyện bằng một lề cực đại. Tất cả các vector nằm trên một mặt của siêu phẳng đều được gán nhãn là -1, và tất cả các

vector nằm trên mặt kia đều được gán nhãn là 1. Các vector huấn luyện gần siêu phẳng nhất gọi là vector hỗ trợ (support vector).

Hình 3.5 (a) Máy hỗ trợ vector tuyến tính đơn giản. (b) Máy hỗ trợ vector (đường nét đứt) và máy hỗ trợ vector hồi quy (đường nét liền). Những vòng tròn biểu diễn dữ liệu chưa được gán nhãn.

Nói chung, SVMs cho phép chiếu dữ liệu huấn luyện gốc trong không gian X sang một không gian đặc trưng F nhiều chiều hơn thông qua một phép phân Mercer K. Nói cách khác chúng ta có tập các bộ phân lớp như sau:

ƒ(x) = (Σ αiK(xi, x)) (3.8)

i=O

Khi K thỏa mãn điều kiện Mercer [12] thì K(u, v) = (u). (v) trong đó : XY và “” là phép tích trong (inner product). Ta có thể viết lại như sau:

ƒ(x) = w. (x), trong bó w = Σ αi(xi)

i=O

(3.9)

Do vậy, bằng cách sử dụng K chúng ta có thể ánh xạ dữ liệu huấn luyện sang một không gian đặc trưng (thường là nhiều chiều hơn). Siêu phẳng lề cực đại được chỉ ra trong biểu thức 3.8. Sau đó SVM tính các i tương ứng với siêu phẳng có lề cực đại trong không gian F. Khi chọn các hàm nhân khác nhau thì có thể ánh xạ dữ liệu huấn luyện từ không gian X sang F sao cho các

siêu phẳng trong F sao cho các siêu phẳng trong F tương ứng với các đường biên quyết định phức tạp hơn trong không gian gốc X.

Hai hàm nhân thường sử dụng là hàm nhân đa thức K(u, r) = (u. r + 1)p tạo ra đường biên đa thức bậc p trong không gian đầu vào X và hàm nhân radial basis fuction K(u, v) = e–y(u–v).(u–v) tạo đường biên bằng cách định vị trọng số Gauss dựa trên các dữ liệu huấn luyện chính. Trong hình

3.6 minh họa đường biên quyết định trong không gian đầu vào X của một SVM sử dụng hàm nhân đa thức bậc 5. Đường biên quyết định được làm cong trong không gian X tương ứng với siêu phẳng lề cực đại trong tập thuộc tính F.

Các tham số i xác định SVM có thể được tìm trong hàm đa thức thời gian bằng cách giải quyết bài toán tối ưu lồi[42]:

arg maxα Σi α — 1 Σi,j αiαjyiyjK(xi, x)

với : i > 0 i=1…n

3.2.2.2 Máy vector hỗ trợ sử dụng phương pháp transduction

(3.10)

Giả sử tập dữ liệu huấn luyện đã được gán nhãn và bài toán đặt ra là tạo ra một bộ phân lớp thực hiện tốt trên tập dữ liệu kiểm tra chưa biết. Thêm vào trong phương pháp qui nạp thông thường, SVMs có thể sử dụng cho bài toán transduction. Đầu tiên là cho tập dữ liệu đã gán nhãn và chưa gán nhãn. Bài toán học là phải khai báo các nhãn tới các dữ liệu chưa gán nhãn càng chính xác càng tốt. SVMs có thể thực hiện phương pháp transduction bằng cách tìm các siêu phẳng làm cực đại hóa lề liên quan đến dữ liệu đã gán nhãn và chưa gán nhãn. Ví dụ được thể hiện ở hình 3.5b. Gần đây, các transduction SVM(TSVM) còn được sử dụng để giải quyết bài toán phâp lớp văn bản [37][38] đã đạt được một số tiến bộ trong việc thực hiện cân bằng tỉ số độ chính xác/độ hồi phục (precision/recall) trên các SVM qui nạp.

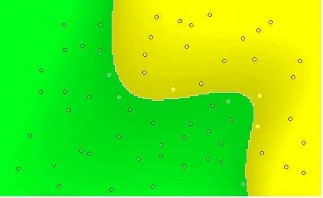
Hình 3.6 Máy hỗ trợ vector sử dụng hàm nhân đa thức bậc 5.

Không giống SVM, TSVM có độ phức tạp thời gian đa thức, chi phí để tìm được hướng giải quyết cho TSVM tăng lên theo hàm mũ cùng với sự tăng của dữ liệu chưa được gán nhãn. Bằng trực quan, ta phải gán tất cả các nhãn có thể cho dữ liệu chưa gán nhãn, và mỗi một nhãn phải tìm một siêu phẳng có lề cực đại. Do vậy sẽ sử dụng thuật toán xấp xỉ thay thế. Ví dụ, Joachims sử dụng dạng tìm kiếm quỹ tích để gán nhãn và tái gán nhãn cho dữ liệu chưa được gán nhãn để cải tiến kích thước của lề.

3.2.3 Version space‌

Cho tập dữ liệu huấn luyện đã gán nhãn và hàm nhân Mercer K, khi đó sẽ có một tập các siêu phẳng chia dữ liệu thành vào không gian thuộc tính F. Tập các giả thuyết phù hợp như vậy gọi là version space [39]. Nói cách khác, giải thuyết f là trong version space nếu với mọi dữ liệu huấn luyện xi có nhãn yi thì f(xi)>0 nếu yi=1 và f(xi)<0 nếu yi=-1. Tổng quát hơn:

Định nghĩa 3.5.1: Cho tập các giả thuyết:

1 = {ƒ|ƒ(x) = w.(s) trong bó wW} (3.11)

"w"

Trong đó không gian tham số W sẽ tương ứng với không gian F. Version space V được định nghĩa như sau:

V = {ƒ1|i{1 … n}yi ƒ(xi) Σ 0} (3.12)

Chú ý rằng khi 1 là tập các siêu phẳng, sẽ có một song ánh giữa vector w

vào giả thuyết f trong 1. Do vậy V sẽ được định nghĩa lại như sau:

V = {wW| "w" = 1, yi(w. (xi)) Σ 0, i = 1 … n} (3.13)

Định nghĩa 3.5.2: Kích thước hay diện tích của version space Area(V) là diện tích bề mặt của siêu khối cầu khi "w" = 1.

Lưu ý rằng version space chỉ tồn tại khi dữ liệu huấn luyện là tách rời tuyến tính trong không gian thuộc tính. Như đã đề cập trong phần 3.2.2.1, hạn chế này không giới hạn như lúc đầu ta tưởng.

Tồn tại sự đỗi ngẫu giữa không gian thuộc tính F và không gian tham số W[43][28] mà chúng ta sẽ áp dụng cho phần sau: các điểm trong F tương ứng với các siêu phẳng trong W và ngược lại.

Vì định nghĩa các điểm trong W tương ứng với các siêu phẳng trong F, ta sẽ quan sát một trường hợp dữ liệu huấn luyện xi trong version space giới hạn các siêu phẳng tách rời nhau vào những bộ mà phân lớp xi một cách chính xác. Thực tế, chúng ta có thể chỉ ra rằng, tập các điểm có thể cho phép w trong W bị giới hạn nằm trong một phía của một siêu phẳng trong W. Hơn nữa, để chỉ ra các điểm trong F tương ứng với siêu phẳng trong W, giả sử cho dữ liệu huấn luyện mới xi có nhãn yi, sau đó bất kỳ siêu phẳng phân chia nào cũng phải thỏa mãn yi(w. (xi)) Σ 0. Bây giờ thay vì chỉ coi w như là một vector trong siêu phẳng F thì ta nghĩ rằng (xi) cũng là vector trong không gian W. Do đó yi(w. (xi)) Σ 0 là nửa không gian trong W. Lại có

w. (xi) = 0 là một siêu phẳng trong W mà nó đóng vai trò như một trong

những đường biên của version space V. Lưu ý rằng version space là một miền đã được kết nối trên bề mặt của một siêu khối trong không gian tham số. Hình

3.7 là một ví dụ.