Lựa chọn hệ thống bài tập, hướng dẫn giải và giải bài tập vật lý về dòng điện xoay chiều - 10

Tính Pmax.

Các mối liên hệ cần xác lập:

U 2

 Công suất

P  UI cos  R .

Z 2

 Vì U và R không thay đổi nên Pmax khi Zmin.

R2  Z  Z



2

L C

 Vì Z   Zmin khi ZL = ZC, tức là trong mạch xảy ra

hiện tượng cộng hưởng điện: 2 LC  1

 4 2 f 2 LC  1

 Tần số

f  1 2 LC

U 2

 Công suất cực đại của mạch:

Pmax  R

Tiến trình hướng dẫn học sinh giải:

Hoạt động của giáo viên

Hoạt động của học sinh
- Biểu thức tính cường độ dòng	- I  U , cos  R Z Z U 2 - P  UI cos  R Z 2 - Pmax khi Zmin. Vì Z  R2  Z  Z 2  Zmin khi L C ZL = ZC, tức là trong mạch xảy ra hiện tượng cộng hưởng điện. - Khi xảy ra cộng hưởng điện thì 2 LC  1  4 2 f 2 LC  1 1  Tần số f  2 LC - Vì Zmin = R nên: U 2 U 2 Pmax  Z 2 R  R min
điện hiệu dụng theo định luật Ohm
và biểu thức hệ số công suất.
- Công suất của mạch P  UI cos
, thay hai biểu thức bên vào P thì
biểu thức công suất P được viết
lại thế nào?
- Theo đề bài, U và R không đổi, P
đạt giá trị cực đại khi nào?
- Từ lý luận đó, hãy tính tần số f
để công suất của mạch đạt cực
đại.
- Tính giá trị cực đại đó của công
suất.

Có thể bạn quan tâm!

• Bài Tập Về Cộng Hưởng Điện: Bài 1:
• Bài Tâp Về Hai Đoan Mach Có Điên Ap Cùng Pha, Vuông Pha. Bài 1:
• Bài Tập Về Công Suất Của Đoạn Mạch R, L, C Mắc Nối Tiếp: Bài 1
• Dạng 6: Xác Định Giá Trị Cực Đại Của Điện Áp Hiệu Dụng Khi Thay Đổi L, Hoặc C, Hoặc F.
• Lựa chọn hệ thống bài tập, hướng dẫn giải và giải bài tập vật lý về dòng điện xoay chiều - 12
• Lựa chọn hệ thống bài tập, hướng dẫn giải và giải bài tập vật lý về dòng điện xoay chiều - 13

Xem toàn bộ 161 trang tài liệu này.

Bài giải:

Công suất của mạch:

P  UI cos  U R

2

Z 2

Vì U không đổi, R không đổi nên Pmax khi Zmin

R2  Z  Z



2

L C

Ta có Z  , nên Zmin khi ZL = ZC, tức là trong mạch có

cộng hưởng điện:

2 LC  1

 4 2 f 2 LC  1

2 LC

2 0,519. 

104

f  1  1

 Tần số

 70, 7

(Hz).

Công suất cực đại của mạch:

Bài 3:

U 2

 Z

Pmax 2

min

2 2

U

U

R  R2 R  R

 1002

50

 200 (W).

Tóm tắt:

104

C  

R = 100

u  U 2 cos100 t (V)

L thay đổi, khi L = Lo thì Pmax = 484W

a. Lo = ? , U = ?

b. biểu thức i = ?

Các mối liên hệ cần xác lập:

U 2

 Công suất

P  UI cos  R .

Z 2

 Vì U và R không thay đổi nên Pmax khi Zmin.

R2  Z

Lo C

 Z



2

 Z  , Zmin khi ZLo = ZC, trong mạch có hiện tượng

o

cộng hưởng điện: 2 L C  1

 Lo

 1

Pmax .R

2C

 Công suất cực đại

2

U

Pmax  R

điện áp hiệu dụng U  .

 Vì xảy ra hiện tượng cộng hưởng điện nên i và u đồng pha i = 0.

Tìm

I  Uo

o R

 biểu thức cường độ dòng điện trong mạch.

Tiến trình hướng dẫn học sinh giải:

Hoạt động của giáo viên

Hoạt động của học sinh
- Biểu thức tính cường độ dòng điện hiệu dụng theo định luật Ôm, công thức tính hệ số công suất. - Thay hai biểu thức bên vào biểu thức công suất P = UIcos thì P	- I  U , cos  R Z Z U 2 - P  UI cos  R Z 2

- Pmax khi Zmin. Vì Z  R2  Z  Z 2 nên Z khi Lo C min ZLo = ZC, tức là trong mạch xảy ra hiện tượng cộng hưởng điện. - Khi trong mạch xảy ra cộng hưởng điện thì 2 L C  1  L  1 o o 2C 2 - P  U  U  P .R max R max - i  Io cos100 t  i  - Vì xảy ra cộng hưởng điện nên u và i đồng pha  i  u  0 . Áp dụng định luật Ôm: I  Uo o R
	- Vì U và R không đổi nên P đạt
	giá trị cực đại Pmax khi nào?
	- Từ lý luận đó, hãy tính hệ số tự
	cảm Lo để công suất đạt giá trị cực
	đại.
	- Biểu thức công suất cực đại
	được viết lại thế nào? Từ đó, hãy
	tính điện áp U hiệu dụng.
	- Yêu cầu học sinh viết dạng của
	biểu thức cường độ dòng điện
	trong mạch.
	- Tính pha ban đầu của i khi trong
	mạch xảy ra cộng hưởng điện, và
	tính Io.
	- Có Io và i biểu thức i.

được viết lại thế nào?

Bài giải:

a. Ta có:

I  Io

, cos  R Z

2

U 2

Suy ra công suất của mạch:

P  UI cos  R Z 2

Vì U không đổi, R không đổi nên Pmax khi Zmin

R2  Z  Z



2

L C

Ta có Z  , nên Zmin khi ZL = ZC, tức là trong mạch

có cộng hưởng điện:

2 L C  1

 Lo

 1

2C

 1

100 2

104

. 

 1

 (H)

Công suất cực đại của mạch:

2

o

U

Pmax  R

Pmax .R

 U  

484.100  220

(V)

b. Vì xảy ra hiện tượng cộng hưởng điện nên i và u đồng pha i = 0

Ta có:

I  Uo

o R

 220

2

100

 3,11 (A)

Bài 4:

Vậy biểu thức i  3,11cos100 t

(A).

Tóm tắt:

L  1 H



C thay đổi được

u  200cos100 t (V)

Khi C = 0,159.10-4F i nhanh pha hơn u một góc

a. biểu thức i = ?

b. P = ? Khảo sát P khi tăng C.

Các mối liên hệ cần xác lập:



4 rad

R  Z  Z

2



L C



2

 i nhanh pha hơn u góc 

4

UC  IZC 

UZC

rad

 Từ công thức

tan  ZL  ZC

R

giá trị R.

 Tìm tổng trở Z 

R2  Z  Z 2

L C

 Áp dụng biểu thức định luật Ohm  Io

 Uo

Z

 Có I và    biểu thức i.

o

i 4

 Áp dụng công thức P = RI2 giá trị công suất P.

 Khảo sát P khi C tăng dần:

2 U 2

U 2 .R

P  RI



 R 

Z 2 

R2   Z

1 

2





 L

 Đạo hàm P theo C.

 Lập bảng biến thiên.

 Vẽ đồ thị P theo C

C 

Tiến trình hướng dẫn học sinh giải:

Hoạt động của giáo viên

Hoạt động của học sinh
- Biểu thức tính cảm kháng, dung kháng? - Theo bài, u  ? , i  ?	- Z  L , Z  1 L C C -   0 , i nhanh pha hơn u một góc   u 4    rad. i 4

- Hãy tính độ lệch pha .

-   

u  i

  

4

- Dựa vào công thức độ

lệch

- tan  tan      ZL  ZC  R  Z  Z

 4  R C L

pha tan, hãy tính giá trị điện  

trở R.

- Yêu cầu học sinh tính tổng

- Z  R2  Z  Z 

2

L C

trở Z.

- Dạng của biểu thức cường

- i  Io cos100 t  i  (A).

U

độ dòng điện tức thời i.

- Tìm Io bằng cách nào?

- Io o

Z

o

- Có I và    biểu thức i

i 4 - P = RI2 (*)

- Biểu thức tính công suất P.

- Hãy biến đổi biểu thức (*)

P  RI 2

2

U

 2 R 

U 2 .R

2

để có P phụ

thuộc điện dung -

Z R2   Z

L

1 







C. 

C 

- Các bước để khảo sát một

- Để khảo sát hàm số y theo x, ta tiến hành các bước sau:

+ Lấy đạo hàm y’ theo x.

hàm số y theo x là gì?

+ Xét cực trị khi y’ = 0.

+ Lập bảng biến thiên.

+ Vẽ đồ thị y theo x.

- Đạo hàm P’ theo C:

- Yêu cầu học sinh khảo sát

RU 2 .

2  1 

Z



2  L 



2

công suất P thay đổi theo điện

 P ' 

C  C 

dung C khi C tăng dần, và rút

2  1

2 

 

ra nhận xét P thay đổi thế nào khi C tăng?

R   ZL  C  

 

' 2RU 2  1 

P  0 

C 2

 ZL  C   0

1

 ZL  C

 0  L  1

C

 C 

 Pmax

1

2 .L

2

 U

R

(cộng hưởng điện)

 0,318.104 (F)

 200 W

Bảng biến thiên:

Vẽ đồ thị P theo C:

Vậy khi C tăng từ 0  0,318.10-4F thì P tăng từ 0 200W.

Khi C tăng từ 0,318.10-4F   thì P giảm từ 200W 100W.

Bài giải:

a. Ta có:

Z  L  100 . 1

L 

 100 ()

1

ZC  C

 1

100 .0,159.104

 200 (V)

Vì u nhanh pha hơn i một góc

 nên   

   

   0  

4

  

i 4

rad

u i 4 4

tan  tan      ZL  ZC  R  Z  Z

 4  R C L

 

2

 R  200 100  100

Tổng trở:

Z 

R2  Z  Z



2

L C

I  Uo  200



2

 (A)

1002  100  2002

 100 

o Z 100 2

Vậy biểu thức i 

2 cos100 t    (A)

 4 

 

b. Công suất P = RI2 = 100.12 = 100W

2 U 2

U 2 .R

P  RI

 R 



Z 2

R2   Z

1 

2





 L C 

RU 2 . 2

 Z  1 

C 2  L

C 

2

 P '   

Đạo hàm P’ theo C:

  1 2 

R2   Z   

 

' 2RU 2 

  L

1 

C  

P  0 

C 2

 ZL  C   0

 C 

1

2 .L

 1



100 2 1

 0,318.104

F

U

2

 Pmax  R

 200 W

Bảng biến thiên:

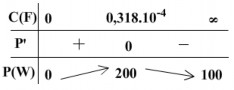
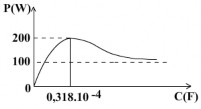
Đồ thị P theo C:

Vậy: khi C tăng từ 0 0,318.10-4F thì P tăng từ 0 200W.

Khi C tăng từ 0,318.10-4F  thì P giảm từ 200W 100W.

Bài 5:

Tóm tắt:

u  80cos100 t

r = 15

(V)



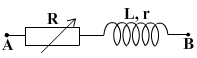
L 1 H

5

a. I = 2A.

Tính R = ?, Ucuộn dây = ?

b. R= ? để Pmax. Tính Pmax = ?

R = ? để

P

R

max

. Tính

P  ?

R

max

Các mối liên hệ cần xác lập:

 Áp dụng công thức, tính cảm kháng

ZL  L

 Tính điện áp hiệu dụng U của toàn mạch: U  Uo

2

 Từ biểu thức định luật Ohm Tổng trở của toàn mạch:

Z  U



R  r  Z



2

2

L

I

(1)

 Z 

(2)

 Từ hai biểu thức (1) và (2) giá trị của biến trở R.

 Điện áp hiệu dụng giữa hai đầu cuộn dây:

r 2  Z 2

L

Ucuộn dây = IZcuộn dây  I

 Công suất tiêu thụ trên toàn mạch:

P  I 2  R  r    

U 2  R  r  U 2

R  r 2  Z 2 Z 2

L

  Z 2 

 R  r  L

R  r

Pmax khi

 R r   L  min

 R  r 

Áp dụng bất đẳng thức Cô-si với hai số không âm:

 R  r 

L

R  r

Z 2

Z 2

 R  r   L  2

R  r

(hằng số)

 Z 2  Z 2

Nên

 R  r   L  min khi R  r  L

 R  r 



R  r

U 2

R  r  ZL  R  ZL  r  Pmax  2 R  r 

 Công suất tiêu thụ trên R:

2 U 2.R U 2 .R U 2

L

PR  I R   R  r 2  Z 2



L

R2  2Rr  r 2  Z 2

 r2  Z 2

L



R

R

 2r

 r2  Z 2   r 2  Z 2 

Pmax 

R  L  2r  min

 R L  min (vì 2r là hằng

 R   R 

r2  Z 2

L

số) Tương tự, áp dụng bất đẳng thức Cô-si với hai số không âm:

2 2

  r  Z 

2  2 

2  

  U 2

RL

R

R r ZL R

PR max

2 R  r 

Tiến trình hướng dẫn học sinh giải:

Hoạt động của giáo viên

Hoạt động của học sinh
- Biểu thức tính cảm kháng và điện áp hiệu dụng toàn mạch.	- Z  L ; U  Uo L 2

Xem tất cả 161 trang.