Vietnamese linking grammar model

The symbol for the set of all correct dependency graphs of the sentence S with the set of dependencies R is GS. This can be considered as a single-layer dependency model.

Dependency models according to the Prague school [109] allow for multi-layer dependencies, so it is possible to model semantic or morphological information while maintaining the properties of the dependency tree.

1.3.2 Properties of the dependent tree

The following are the properties of the dependency tree, the results of sentence analysis according to the dependency model. These properties reflect the characteristics of Tesnière’s original dependency model [82].

The dependency tree G = (V, A) always satisfies the following properties:

Root property: Root node ROOT does not depend on any node.
Frame property: On all words of the sentence: V = VS.
Connected: A dependency tree is a weakly connected graph.
A single head: each dependent word has only one central word.
No cycle: The dependency graph is connected.
Properties of arc numbers: The graph of dependence G = (V, A) satisfies the property:|A| = |V| – first
Projective properties.
Each arc in a tree is projective if there is a path from the center to every word that lies between the two endpoints of the arc.
A dependency tree G = (V, A) is a projective dependency tree if :
1. It is a dependency tree
1. All (wi , r, wj) A is projective

Otherwise G is a non-projective dependent tree

A projective dependent tree is flat if it is possible to draw all the arcs of the tree in the upper space of the sentence without any intersecting arcs.

Compare dependency grammar and context-free grammar.

In [57], [62] proved that the dependent grammar is weakly equivalent to the context-free grammar.

The basic difference between dependent grammars and context-free grammars is that the dependency structure represents the central-dependency relationship between words, classified by functional domains such as subject or complement. , while representing the context-free type of grouping words into phrases and classifying them by structural domains such as nouns and verbs.

However, for the same sentence, the dependency tree is much simpler than the structure tree because it contains only as many nodes as the number of words in the sentence +1.

Dependency grammar is well suited for languages with free word order, because many dependency models do not require projective properties. The fact that the dependent grammar can represent the dependence on word morphology (gender, number, way…) is also a compelling reason for the above statement.

The dependency grammar can represent semantic information if extended models are used. According to Fox [55], the dependency model is very convenient for machine translation problems because of its small crossing measure.

In contrast, the dependency model is difficult to solve the language generation problem because in the general case, it is difficult to combine the dependency trees into a larger dependency tree.

The classical dependency model does not solve the coordination problem due to the one-word-central nature of the dependency relationships. To solve this problem, it is necessary to use some extended forms of dependent grammar such as Dependency Categorical Grammar [103], or dependency with many central words according to the word grammar model. (Word Grammar) by Hudson [65], [114].

1.4. Linking grammar

1.4.1. The concept of linking grammar

The associative grammar model was introduced by Sleator and Temperley [111] in 1991. Up to now, this model has been developed and used in many different fields because it has described many phenomena of English as well as English. many other languages. English Link Analyzer allows analysis of many long sentences, compound sentences. Link analysis results are commonly used in systems that allow information extraction, machine translation, and language generation.

A linking grammar consists of a set of words (which can be thought of as the set of terminators of the grammar), each of which has a binding request. A sequence of words is a correct sentence if there exists a way to draw arcs (links) between words such that the following conditions are satisfied:

Planarity: links do not intersect (when drawn above words).
Connectivity: links are capable of connecting all words in a sentence together.
Satisfaction: the links satisfy the association requirements of each word in the sentence
Exclusion: no two links can connect the same word pair.

The association requirements of each word are contained in a dictionary. The dictionary is represented in a computer readable form. In Table 1.1 below is an example of a mini associative dictionary:

Table 1.1. Example of a dictionary

Vocabulary	Recipe
why	THT+
boy	SV+
Are not	RnV+
next	(RnV- or()) &(SV-)&(THT- or ())

Maybe you are interested!

In the dictionary, each word has an associated formula. With the form of such a link formula, the 5th requirement should be added as follows:

5.Calculation: When the connections of a formula are traversed from left to right, the words it connects to progress from near to far.

The graph in Figure 1.6 shows the association requirements that are satisfied in the question “Why don’t you come?”.

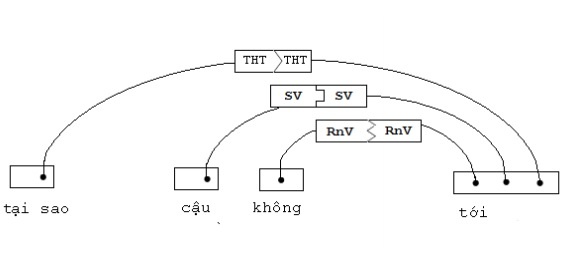
Figure 1.6. The grammatically correct sentence “Why didn’t you come”

The use of formulas to represent a dictionary of associative grammars is close to the phenomena of natural language, but is cumbersome for describing the association analysis algorithm. In [111], another way of representing a linking grammar was introduced, called disjunct.

Each word of a grammar has a set of colloquial forms associated with it. Each selection corresponds to a way that satisfies the association requirements of a word. A selection form consists of two ordered lists of connection names: a list on the left and a list on the right. The list on the left includes the connections that join to the left of the current word (connections ending with – in the linking formula), and the list on the right contains the connections that join to the right of the word. current word (connections ending with + in link formulas). One type of recruitment is denoted:

((L1, L2,…, Lm) (Rn, Rn-1,…, R1))

Where L1, L2,…, Lm are connections to the left and Rn, Rn-1,…, R1 are connections to the right. The number of connections in each list can be zero. The following + or – sign can be omitted from the name of the connection when using the join form, because the direction is implicit in the join form.

To satisfy the association requirements of a word, one of its selection forms must be satisfied. To satisfy a selection, all of its associations must be satisfied by the appropriate connections. Words that L1, L2, … link to stand to the left of the current word, and are monotonically reduced in distance from the current word. Words that R1, R2, … link to stand to the right of the current word, and monotonically increase the distance from the current word.

The selection form is the equivalent of a formula. Each formula corresponds to a set of selection forms. For example, the formula (A- or ( )) & D- & (B+ or ( )) & (O- or S+) given in [111] corresponds to the following eight forms:

((A,D) (S,B))

((A,D,O) (B))

((A,D) (S))

((A,D,O) ( ))

((D) (S,B))

((D,O) (B))

((D) (S))

((D,O) ( ))

When analyzing sentences, the association analyzer will convert the formulas in the dictionary into the corresponding vacancies and find a combination of recruitment forms that satisfy the above requirements, if the sentence is syntactically correct.

A subtype of a recruitment type is constructed by deleting one or more connections at the beginning and the end of the two join lists of that recruitment type.

For example, the non-empty subjunctive forms of the colloquial form ((O)(EoPp)) of Vietnamese concrete nouns (“brother”, “sister”, “dad”, “mother”…) are: ( (O) (EoPp)), ((O) ( )), (( ) (EoPp)).

A fat connector is a connection that connects not only words but also phrases. Therefore, it can be understood that the collection contains a large connection consisting of two lists left and right, each list containing a subset.

For example, Connection <(O) (EoPp)> is a large connection. It can be a component of some form, for example (( )(<(O) (EoPp)>))

In the example in Figure 1.7, the connection F = <(O) (EoPp)> connects to the phrase consisting of the word “and”, the word “brother” and the word “sister”. The two words “brother” and “sister” share the same form as ((O) (EoPp)). Large connections are used to connect elements that have the same function in a sentence, avoiding intersecting links. The selection form for the word “and” becomes ((F, O)(EoPp, F)). Note that, in the dictionary, the word “and” does not have an anthology ((O)(EoPp)) that belongs to the word “bro” and the word “sister”. Since the great connection F is established between the word “and” and the words “brother”, “sister”, the word “and” has played the role of both the word “brother” and the word “sister”. Specific application problems of large connections will be discussed in section 3.3.

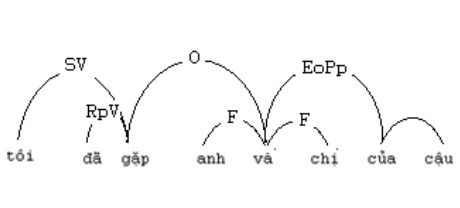
Figure 1.7. Great connection of the word “and”

Associative grammar is classified as dependent [70], because the model also represents relationships between words in a sentence. However, linking grammar has many differences.

Non-directive linking: The linking grammar has no concept of “rule”, “dependency”. The connections are not directional, the two words linked together are equal. This model is only interested in whether the direction of the link is left or right. This is the basic difference between dependency grammar and linking grammar.

Labeled Links: If in the dependency grammar, the dependencies do not necessarily have labels, then the links in the association grammar must have labels.