Context-Free Grammar For Natural Language Representation

Vietnamese linking grammar model - 3

CHAPTER 1

OVERVIEW OF PHARMACOLOGICAL MODELS FOR NATURAL LANGUAGE

According to Jurafsky [70], grammatical relations are ways of formalizing the ideas of traditional grammars such as subject or complement and other relationships. Many grammar models have been proposed according to the following approaches: structure (constituency), grammatical relation (grammar relation), subcategorization (subcategorization) or dependency (dependency). The two most popular approaches today are structure and dependency. This chapter will introduce common grammar models and the position of associated grammars in the system of grammar models.

1.1. Context-free grammar and structure approach

The first problem when describing syntactic rules is to represent the rules for grouping words into sentences. If Vietnamese grammar [28] stipulates that a sentence must contain a core (single or compound), a single core must contain a subject and predicate with the subject always preceded by the predicate, then the problem of describing syntactic rules turns into a problem of creating structures and making rules about the location of structures.

The model that allows studying the creation of structures recursively is the context-free grammar model. This formal model is equivalent to the BNF (Backus Naur Form) standard form of the programming language.

The model that allows studying the creation of structures recursively is the context-free grammar model. This formal model is equivalent to the BNF (Backus Naur Form) standard form of the programming language.

1.1.1. Context-free grammar for natural language representation

Maybe you are interested!

• Vietnamese linking grammar model - 1
• Vietnamese linking grammar model - 2
• Lexicalization Probabilistic Context-Free Grammar
• Approach Through Stroke Structure And Unified Grammar
• Vietnamese linking grammar model - 6

A context-free grammar consists of a set of rules or productions, each representing the way in which the symbols of the language are grouped and ordered, and a lexicon consisting of words and symbols.

Example: A production set of Vietnamese context-free grammar with meanings of non-terminating symbols: S – sentence, NP – noun, VP – verb, N – noun, V – verb, P – pronoun.

S → NP VP

NP → P

NP → N P

VP → V NP

This production is able to describe the syntactic structure of the sentence “I love my mother” with the pronoun “I”, the noun “mother” and the verb “to love”.

Formally, the context-free grammar can be described as follows:

Definition 1.1. [70] A context-free grammar is a set of 4 G = (N, Σ, R, S), where:

N: non-terminating symbol set (variable).

Σ: the end symbol set (does not intersect with N).

R: rule set, or production set of the form A → β, A is a non-terminating symbol, β is a string consisting of a finite number of symbols on an infinite set (Σ ∪ N)* (the set of all strings on the alphabet Σ) ∪ N).

S: first symbol.

In the context-free grammar model, the parsing problem is the problem of finding the structure tree for the input sentence. Each node of the structure tree is labeled a non-terminating symbol representing a structure. According to [56], the structure tree represents the following information about the syntax:

• Linear order of words in a sentence.
• Names of syntactic categories of words and groups of words.
• Hierarchical structure of syntactic categories.

The parsers follow the classical context-free grammar model mainly according to two methods CYK (Cocke – Younger – Kasami) and Earley. There have been Vietnamese parsers built according to CYK [12], Earley [5], [27] methods with appropriate improvements.

In Figure 1.1 is a structure tree for the sentence “I like chicken feet”. This structure tree, if not counting the labels of the leaf nodes, is the same as the structure tree of the sentence “I like silk shirt”, however, if translated into English, these two sentences must be translated differently. The relationship between nouns indicating animal body parts and nouns indicating animals is a possessive relationship, so “chicken feet” must be understood as “chicken’s feet”, while the relationship between “coat” and “silk” ” is the relationship in terms of material “silk shirt”. The context-free model does not yet show this relationship.

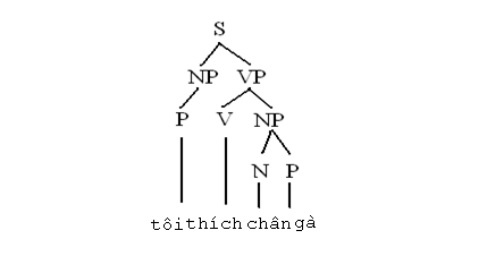
Figure 1.1. Structure tree of the sentence “I like chicken feet“.

The ambiguity problem is one of the most complex problems that parsers have to deal with. According to [70], in the parsing phase, the problem of ambiguity is structural ambiguity. Assume that we only consider a single sentence, that is, a sentence with only one core, and ignore the problem of ambiguity from the type. Structural ambiguity occurs when a sentence has more than one parse tree. In Figure 1.2 are two different tree structures for the sentence “They won’t ship the goods tomorrow” (example sentence in [20]) with context-free grammar.

S → NP VP

NP → P

VP → R VP | R R V N PP PP PP-TMP | VP PP | V NP PP

PP → E NP

PP-TMP →E NP Meaning of the symbols: S – sentence, NP – noun, VP – verb, PP – preposition, N – noun, V – verb, P – pronoun, R – auxiliary, E – preposition , PP-TMP – preposition of time.

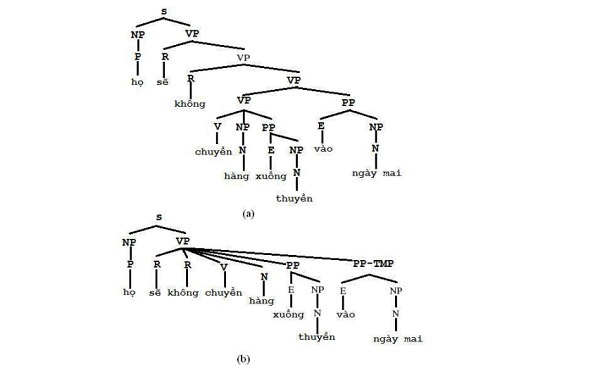
Figure 1.2. Two sentence structures of the sentence “They won’t ship the goods to the boat tomorrow“.

One of the first approaches to solving ambiguity when parsing on context-free grammar models is the probabilistic context-free grammar model. (Probabilistic Context Free Grammar).

1.1.2. Probabilistic context-free grammar

In the probabilistic context-free grammar model, each rule is appended with a probability indicating how often the rule is used in the tree of the structure.

Definition 1.2. [70] Probabilistic context-free grammar is quadruple

N: non-terminating symbol set (variable).

Σ: the end symbol set (does not intersect with N).

R: rule set, or production set of the form A → β | p |, where A is a non-terminating symbol, β is a string consisting of a finite number of symbols on an infinite set (Σ ∪ N)*, p is the number in the interval [0,1] representing the probability Pr ( β | A ).

S: first symbol.

The probability of a structure tree is the product of the probabilities of the n rules used to expand its n interior nodes:

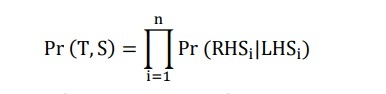
LHSi and RHSi are the left and right sides of the production used for the ith node of the structure tree.

The selected tree is the tree with the greatest probability [41]

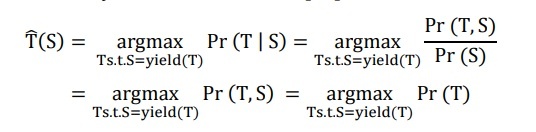
The expression T.s.t.S = yield(T) requires a calculation on all Structural trees T that results in a sentence S.

In the ideal case, if there is a large enough treebank, the probability of each rule can be calculated by the formula:

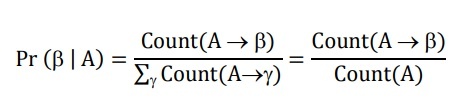
The problem is that when starting the work, the treebank is not there yet or not big enough. Therefore, it is necessary to choose a corpus, analyze its sentences to gradually add to the tree bank and calculate the above probabilities. We face another problem, when a sentence can have multiple analyses: which one should be chosen? Solving the ambiguity problem falls into the “chicken and egg” situation.