Phương Pháp Tô Màu Dựa Theo Đường Biên

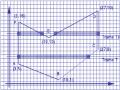
Lưu đồ thuật toán scan - line

Begin

Tạo danh sách tất cả các cạnh (ET) của đa giác.

i = ymin

Có thể bạn quan tâm!

Xem toàn bộ 106 trang tài liệu này.

i < ymax No

Yes

Cập nhật danh sách các cạnh kích họat AET

Tìm hoành độ giao điểm và sắp xếp theo thứ tự tăng dần

Tô mẫu các đoạn giao được tạo bởi từng cặp hoành độ kế tiếp nhau

Cập nhật lại thông tin của các cạnh để sử dụng cho dòng quét kế tiếp

i = i + 1

End

2.3.3. Phương pháp tô màu dựa theo đường biên

Bài toán đặt ra : Cần tô màu một vùng nếu biết được màu của đường biên vùng tô và một điểm nằm bên trong vùng tô.

Ý tưởng : Bắt đầu từ một điểm nằm bên trong vùng tô, kiểm tra các điểm lân cận của nó đã được tô với màu muốn tô, hay điểm lân cận có màu trùng với màu biên không ? Nếu cả hai trường hợp đều không phải thì ta sẽ tô điểm đó với màu muốn tô. Quá trình này được lặp lại cho đến khi không còn tô được nữa thì dừng (xem hình 2.8).

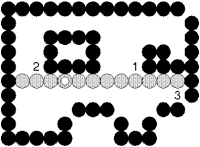
Hình 2.8 : Tô màu theo đường biên.

Có 2 quan điểm về cách tô này. Đó là dùng 4 điểm lân cận (có thể gọi là 4 liên thông) hay 8 điểm lân cận (8 liên thông) (xem hình 2.9).

(x,y-1)

(x-1,y)(x,y)(x+1,y)

(x,y+1)

Hình 2.9 : 4 liên thông và 8 liên thông.

Cài đặt minh họa thuật toán 4 liên thông

Procedure Boundary_fill ( x,y, mauto, maubien :integer); var mau_ht : integer;

begin

mau_ht:= getpixel(x, y);

if (mau_ht <> mauto) and (mau_ht <> maubien) then begin

end;

putpixel(x,y,color);

Boundary_fill ( x+1,y, mauto, maubien ); Boundary_fill ( x-1,y, mauto, maubien ); Boundary_fill ( x,y+1, mauto, maubien ); Boundary_fill ( x,y-1, mauto, maubien );

Nhận xét :

- Thuật toán có thể không chính xác khi có một số điểm nằm trong vùng tô có màu là màu cần tô của vùng.

- Việc thực hiện gọi đệ qui làm thuật toán không thể sử dụng cho vùng tô lớn ( tràn stack).

- Có thể khắc phục việc tràn stack bằng cách giảm số lần gọi đệ qui. Khởi đầu điểm (x,y) là điểm có vị trí đặc biệt trong vùng tô, sau đó, gọi đệ qui các điểm lân cận của (x,y) (xem hình 2.8).

(500,200)

(100,100)

(100,400)

Hình 2.10: Tam giác với 3 tọa độ đỉnh.

Ví dụ 1: Trong hình 2.10, ta có thể xét điểm (x,y) có tọa độ là (498, 200). Với điểm khởi đầu này thì chỉ cần xét 3 điểm lân cận là (x-1,y), (x,y-1), (x,y+1). Khi đó thủ tục tô màu theo đường biên được viết lại như sau :

Procedure Boundary_fill ( x,y,mauto, maubien :integer); var mau_ht : integer;

begin

mau_ht:= getpixel(x,y);

if (mau_ht <> mauto) and (mau_ht <> maubien) then begin

end;

putpixel(x,y,color);

Boundary_fill ( x-1,y, mauto, maubien ); Boundary_fill ( x,y+1, mauto, maubien ); Boundary_fill ( x,y-1, mauto, maubien );

Ví dụ 2: Trong hình 2.10, ta có thể xét điểm (x,y) có tọa độ là (102, 102). Với điểm khởi đầu này thì chỉ cần xét 2 điểm lân cận là (x+1,y), (x,y+1). Khi đó thủ tục tô màu theo đường biên được viết lại như sau :

Procedure Boundary_fill ( x,y,mauto, maubien :integer); var mau_ht : integer;

begin

mau_ht:= getpixel(x,y);

if (mau_ht <> mauto) and (mau_ht <> maubien) then begin

end;

putpixel(x,y,color);

Boundary_fill ( x+1,y, mauto, maubien ); Boundary_fill ( x,y+1, mauto, maubien );

- Một cải tiến khác : không cài đặt đệ qui mà tô theo từng dòng (xem hình 2.11).

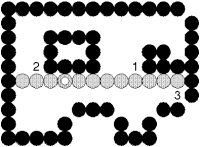
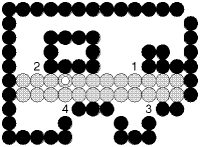
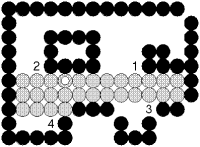
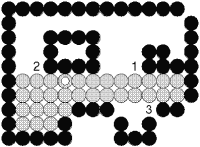
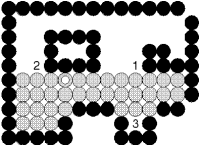
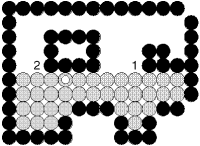
Hình 2.10 : Tô theo từng dòng.

2.4. Tổng kết chương 2

- Sinh viên cần hiểu được khái niệm về các không gian màu. Lưu ý nhiều ở giải thuật tô biên và scan-line.

- Trong scan-line phải đánh dấu các đỉnh đơn điệu và đỉnh cực trị.

- Trong giải thuật tô biên, việc thực hiện gọi đệ qui nhiều lần làm thuật toán không thể sử dụng cho vùng tô lớn (tràn stack). Có thể khắc phục việc tràn stack bằng cách giảm số lần gọi đệ qui. Thực hiện gọi đệ qui tại đỉnh đặc biệt của đa giác.

2.5. Bài tập chương 2

20. Viết chương trình vẽ một đa giác n đỉnh, xét xem một điểm P nào đó có thuộc

đa giác không ?

21. Viết chương trình vẽ một đa giác n đỉnh. Tô đa giác bằng giải thuật tô đơn giản ( Tìm xmin, ymin, xmax, ymax).

22. Viết chương trình vẽ một đường tròn. Tô đường tròn bằng giải thuật tô đơn giản.

23. Viết chương trình vẽ một đa giác n đỉnh. Tô đa giác bằng giải thuật tô biên. Lưu ý cho các trường hợp của đa giác : hình chữ nhật, đa giác lồi, đa giác lõm.

24. Viết chương trình vẽ một đường tròn. Tô đường tròn bằng giải thuật tô biên.

25. Viết chương trình vẽ một đa giác n đỉnh. Tô đa giác bằng giải thuật scan-line.

26. Viết chương trình vẽ một đường tròn. Tô đường tròn bằng giải thuật tô scanline.

27. Viết chương trình vẽ hai đường tròn C1 và C2 cắt nhau. Tô phần giao của hai đường tròn đó. Tô phần bù của C2. Tô phần bù của C1. Lưu ý rằng 3 màu tô này phải khác nhau.

Chương 3 : PHÉP BIẾN ĐỔI TRONG ĐỒ HỌA HAI

CHIỀU

3.1. Tổng quan

Mục tiêu

- Sinh viên cần hiểu được các phép biến đổi cơ bản trong không gian hai chiều. Nắm vững công thức tổng quát của phép biến đổi Affine, từ đó suy ra các phép tịnh tiến, quay...

- Có khả năng lập trình tạo một hình ảnh động trên máy tính

Kiến thức cơ bản cần thiết

Kiến thức toán học : hiểu biết về ma trận, định thức. Các phép toán trên ma trận.

Tài liệu tham khảo

Computer Graphics . Donald Hearn, M. Pauline Baker. Prentice-Hall, Inc., Englewood Cliffs, New Jersey , 1986 (chapters 5, 106-122).

Nội dung cốt lõi

Bản chất của phép biến đổi hình học là thay đổi các mô tả về tọa độ của đối tượng như thay đổi về hướng, kích thước, hình dạng. Do đó, chương này trình bày các phép biến đổi như tịnh tiến, tỉ lệ, phép quay, đối xứng, biến dạng.

3.2. Phép tịnh tiến (translation)

Có hai quan điểm về phép biến đổi hình học, đó là :

- Biến đổi đối tượng : thay đổi tọa độ của các điểm mô tả đối tượng theo một qui tắc nào đó.

- Biến đổi hệ tọa độ : Tạo ra một hệ tọa độ mới và tất cả các điểm mô tả đối tượng sẽ được chuyển về hệ tọa độ mới.

Các phép biến đổi hình học cơ sở là : tịnh tiến, quay, biến đổi tỉ lệ.

Phép biến đổi Affine hai chiều (gọi tắc là phép biến đổi) là một ánh xạ T biến

đổi điểm P(Px, Py) thành điểm Q(Qx, Qy) theo hệ phương trình sau: Qx = a*Px + c*Py + trx

Qy = b*Px + d*Py + try

Hay

x y x y ⎜c

(Q , Q ) = (P , P ). ⎛⎜a

⎝

b ⎞⎟

d⎟

⎠

+ (trx, try)

 Q = P.M + tr

Dùng để dịch chuyển đối tượng từ vị trì này sang vị trí khác.

Nếu gọi trx và try lần lượt là độ dời theo trục hoành và trục tung thì tọa độ điểm mới Q(x', y') sau khi tịnh tiến điểm P(x,y) sẽ là :

x' = x + trx y' = y + try

(trx, try) được gọi là vector tịnh tiến hay vector độ dời (xem hình 3.1). Hay Q = P*M +tr

⎜0

M= ⎛⎜1

⎝

try

0⎞⎟

1⎟

⎠

y O

, tr = (trx, try)

P(x,y)

trx

Q(x',y')

Hình 3.1 : Phép biến đổi tịnh tiến điểm P thành Q.

3.3. Phép biến đổi tỷ lệ

Phép biến đổi tỉ lệ làm thay đổi kích thước đối tượng. Để co hay giãn tọa độ của một điểm P(x,y) theo trục hoành và trục tung lần lượt là Sx và Sy (gọi là các hệ số tỉ lệ), ta nhân Sx và Sy lần lượt cho các tọa độ của P.

x' = x.Sx

y' = y.Sy

- Khi các giá trị Sx , Sy nhỏ hơn 1, phép biển đổi sẽ thu nhỏ đối tượng. Ngược lại, khi các giá trị này lớn hơn 1, phép biến đổi sẽ phóng lớn đối tượng.