Tự cảm của cuộn dây (Self Inductance of a Coil)
o L là Henries
o N là số lần vòng
o Φ là lượng từ thông
o Ι là Amperes
Lưu ý rằng phương trình này chỉ áp dụng cho các vật liệu từ tính tuyến tính.
Ví dụ 2: Từ ví dụ 1, tính toán giá trị của suất điện động cảm ứng tự tạo ra trong cùng một cuộn dây sau một thời gian 10mS Giải pháp ( Solution) Áp dụng công thức:; thay số ta có: V = 500V L |
Có thể bạn quan tâm!
-
Các Tham Số Chính Của Tụ (Main Parameters Of The Capacitor) -
Ký Hiệu Tụ Điện Phân Chuẩn Mỹ Hoặc Anh -
Xác Định Chiều Đường Sức Từ Trong Dây Thẳng -
Cuộn Cảm Song Song Cảm Ứng Trái Cực -
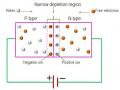
Cấu Trúc Chất Bán Dẫn Loại P Dòng Điện Chảy Trong Chất Bán Dẫn Loại P Như Thế Nào -
Các Đặc Điểm Cơ Bản Của Diode (Basic Characteristics Of Diode)
Xem toàn bộ 264 trang tài liệu này.
Đối với một cuộn dây, thông lượng từ được tạo ra trong lõi : = B.A Trong đó: Φ là thông lượng từ, B là mật độ thông lượng và A là diện tích. Cuộn dây có N vòng, lõi không khí thì
Sau đó, bằng cách thay thế ta có phương trình và thu gọn ta có
o L độ tự cảm tính bằng Henries
o o là tính thấm của không gian trống ( o = 4.π.10-7)
o N là số vòng dây
o A là diện tích vùng lõi bên trong (A = πr 2) tính bằng m2
o L là chiều dài của cuộn dây tính bằng mét
2.3.3. Điện cảm tương hỗ (Mutual Inductance)
Hệ số hỗ cảm hay Điện cảm tương hỗ là sự tương tác của từ trường một cuộn dây này lên cuộn dây khác vì nó gây ra điện áp trong cuộn dây lân cận
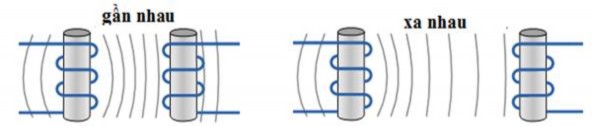
Hình 2. 0-24: Tương hỗ giữa hai cuộn dây
Sự tự cảm tương hỗ giữa hai cuộn dây có thể được tăng lên rất nhiều bằng cách đặt chúng trên một lõi sắt mềm hoặc bằng cách tăng số vòng dây quấn của một trong hai cuộn dây
Phương trình tự cảm tương hỗ
Trong đó:
o µo là độ thấm của không gian trống (4.π.10-7)
o µr là độ thấm tương đối của lõi sắt mềm
o N là số vòng cuộn dây
Ở đây dòng điện chạy trong một cuộn dây L1 thiết lập một từ trường xung quanh chính nó với một số các đường từ trường đi qua cuộn dây hai L2. Do đó, điện cảm tương hỗ lẫn nhau M12 của cuộn dây hai tồn tại đối với cuộn dây một phụ thuộc vào vị trí của chúng đối với nhau và được cho là:
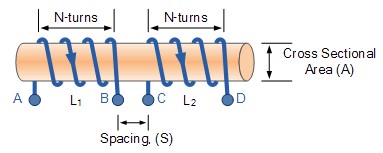
Hình 2. 0-25: Hỗ cảm gây ra bởi hai cuộn dây cùng lõi
M12 = M21 = M
Hệ số tự cảm của mỗi cuộn dây được đưa ra là
Bằng cách nhân chéo hai phương trình trên, điện cảm lẫn nhau, M tồn tại giữa hai cuộn dây có thể được biểu diễn theo độ tự cảm của mỗi cuộn dây
M2 = L1L2
√
Tuy nhiên, phương trình trên giả định rò rỉ thông lượng bằng không và khớp nối từ tính 100% giữa hai cuộn dây, L1 và L2. Trong thực tế sẽ luôn có một số tổn thất do rò rỉ và vị trí, vì vậy khớp nối từ giữa hai cuộn dây không bao
giờ có thể đạt hoặc vượt quá 100%, nhưng có thể trở nên rất gần với giá trị này trong một số cuộn cảm ứng đặc biệt.
√
Giá trị phân số này được gọi là hệ số liên kết và được cho chữ k. Nói cách khác, nếu k = 1 hai cuộn dây được kết hợp hoàn hảo, nếu k> 0,5 thì hai cuộn dây được cho là được ghép chặt và nếu k <0,5 thì hai cuộn dây được cho là được ghép lỏng lẻo
Ví dụ:Khi hai cuộn dây có điện cảm 5H và 4H tương ứng được quấn đồng nhất vào một lõi không từ tính, nó đã được tìm thấy rằng điện cảm lẫn nhau của chúng là 1,5H. Tính hệ số ghép nối tồn tại giữa. Hướng dẫn
√ |
2.3.4. Cuộn cảm nối tiếp (Series inductor)
Cuộn cảm có thể được kết nối với nhau trong một hàng khi chia sẻ một dòng điện chung.
Hình 2. 0-26: Mạch cuộn cảm mắc nối tiếp
Ltđ = Ltotal = L1 + L2 + L3 + … + Ln
Ví dụ: Ba cuộn cảm 10mH, 40mH và 50mH được kết nối với nhau trong một loạt kết hợp mà không có sự tự cảm lẫn nhau giữa chúng. Tính tổng điện cảm của kết hợp chuỗi.
Hướng dẫn
Do mắc nối tiếp:
Ltđ = Ltotal = L1 +
L2 + L3
LT = 10 + 40 + 50 = 100 mH
Dòng cảm ứng đồng bộ (Cumulatively Coupled Series Inductors)
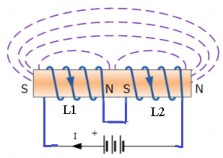
Hình 2. 0-27: Dòng cảm ứng đồng bộ
Khi dòng điện thông qua hai cuộn dây tích lũy cùng hướng, tự cảm của mỗi cuộn dây L1 và L2 nhưng với việc bổ sung M thì
Ltotal = L 1 + L2 + 2M
Ví dụ: Hai cuộn cảm của 10mH tương ứng được kết nối với nhau trong một loạt sự kết hợp sao cho từ trường của chúng giúp lẫn nhau tạo ra sự kết hợp tích lũy. Sự tự cảm lẫn nhau của chúng được đưa ra là 5mH. Tính tổng điện
cảm của kết hợp chuỗi.
Hướng dẫn
Áp dụng công thức:
Ltotal = L 1 + L2 + 2M
Ltotal = 10 + 10 + 2x5 = 30 (mH)
Dòng cảm ứng dị bộ (Differentially Coupled Series Inductors)
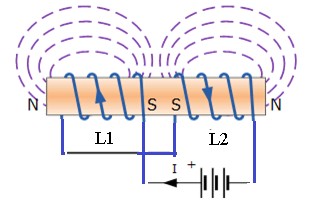
Hình 2. 0-28: Cảm ứng nối tiếp ngược chiều
Ltotal = L 1 + L 2 - 2M
Cùng một dòng điện đi qua mỗi cuộn nhưng theo hướng ngược nhau. Dấu trừ được sử dụng với M khi từ trường của hai cuộn dây được kết nối khác nhau
Ltotal = L 1 + L 2 - 2M
Ví dụ: Hai cuộn dây kết nối trong loạt có một tự cảm của 20mH và 60mH tương ứng. Tổng điện cảm của sự kết hợp đã được tìm thấy là 100mH. Xác định số lượng điện cảm lẫn nhau tồn tại giữa hai cuộn dây giả định rằng chúng dị bộ.
Hướng dẫn
Áp dụng công thức:
M = 20/2 = 10 mH
2.3.5. Cuộn cảm song song (Inductor Parallel)
Cuộn cảm được cho là được kết nối với nhau song song khi cả hai thiết bị đầu cuối của chúng được kết nối tương ứng với mỗi thiết bị đầu cuối của một cuộn cảm khác
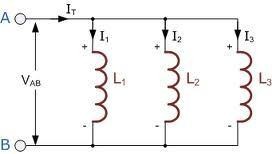
Hình 2. 0-29: mạch cuộn cảm mắc song song
Mạch song song, cuộn cảm tương đương được tính
Khi chỉ có hai cuộn cảm song song, công thức tìm tổng giá trị điện cảm đơn giản hơn và nhanh hơn có thể được sử dụng là:
Ví dụ: Ba cuộn cảm của 60mH, 120mH và 75mH tương ứng, được kết hợp song song mà không có sự tự cảm lẫn nhau giữa chúng. Tính tổng điện cảm của sự kết hợp song song bằng millihenries.
Hướng dẫn:
Áp dụng công thức:
song song hỗ trợ cuộn cảm (Parallel Aiding Inductors)
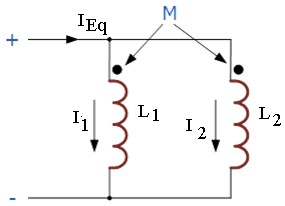
Hình 2.0-30: Cuộn cảm song song có hõ cảm đồng cực
Điện áp trên hai cuộn cảm song song bằng nhau, hai dòng điện, i1 và i2 phải thay đổi sao cho điện áp trên chúng vẫn giữ nguyên. Khi đó, tổng điện cảm, LT ứng hai cuộn cảm trợ song song
Ví dụ: Hai cuộn cảm có tự cảm 75mH và 55mH tương ứng được kết nối với nhau trong hỗ trợ song song. Điện cảm tương hỗ của chúng được đưa ra là 22.5mH. Tính tổng điện cảm của sự kết hợp song song.
Hướng dẫn
Áp dụng công thức:
Thay số vào biểu thức: