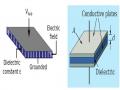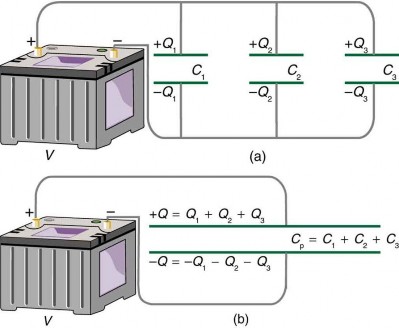
Hình 2.0-17: Mạch tụ điện mắc song song
và các điện tích riêng là Q1 = C1V, Q2 = C2V và Q3 = C3V. Nhập vào các phương trình trước đó, ta có:
CpV = C1V + C2V + C3V
Loại bỏ V, ta được:
Cp = C1 + C2 + C3
Giải quyết (Sulotion) Áp dụng công thức: Cp = C1 + C2 + C3 thay C1 = 1F , C2 = 2F , C3 = 5F vào biểu thức ta có: Cp = 1 + 2 + 5 = 8 F |
Có thể bạn quan tâm!
-
Các Loại Biến Trở Điện Trở Công Suất (Power Resistor) -
Các Tham Số Chính Của Tụ (Main Parameters Of The Capacitor) -
Ký Hiệu Tụ Điện Phân Chuẩn Mỹ Hoặc Anh -
Điện Cảm Tương Hỗ (Mutual Inductance) -
Cuộn Cảm Song Song Cảm Ứng Trái Cực -
Cấu Trúc Chất Bán Dẫn Loại P Dòng Điện Chảy Trong Chất Bán Dẫn Loại P Như Thế Nào
Xem toàn bộ 264 trang tài liệu này.
2.3. Cuộn cảm
2.3.1 Khái niệm :
Cuộn cảm là linh kiện điện thụ động bao gồm một cuộn dây được thiết kế để tận dụng mối quan hệ giữa từ trường và dòng điện chạy qua cuộn dây.
Ở dạng cơ bản nhất của nó, một cuộn cảm không là gì ngoài một cuộn dây quấn quanh một lõi ở trung tâm. Đối với hầu hết các cuộn dây, dòng điện (i) chảy qua cuộn dây sẽ tạo ra một thông lượng từ (NΦ) tỷ lệ thuận với dòng điện này.
Cuộn cảm được hình thành với dây quấn chặt quanh lõi rắn có thể là một thanh hình trụ thẳng hoặc vòng lặp liên tục hoặc vòng để tập trung từ thông của chúng.
Dòng điện chạy trong ruột dây dẫn điện sẽ tạo ra một từ trường có thể gây ảnh hưởng đến vùng xung quanh nó. Điều này được gọi là hiệu ứng điện từ của dòng điện, được phát hiện vào năm 1820 bởi Hans Christian Oersted (14 tháng 8 năm 1777 - 9 tháng 3 năm 1851) là một nhà vật lý và nhà hóa học người Đan Mạch. Do hiệu ứng này, hai dây dẫn song song trong đó dòng điện chạy theo cùng một hướng thu hút lẫn nhau. Ngược lại, chúng đẩy xa nhau nếu dòng chảy theo hướng ngược nhau.
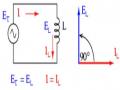
quy tắc vít tay phải (the right-handed screw rule)
Chiều của các đường sức từ có thể được xác định chắc chắn bởi cái gọi là quy tắc vít tay phải: Nếu chiều dòng điện chạy vào cuộn dây được so sánh với chiều tiến của một ốc vít bên tay phải thì chiều của các đường từ trường được định hướng theo cùng chiều quay của ốc vít.
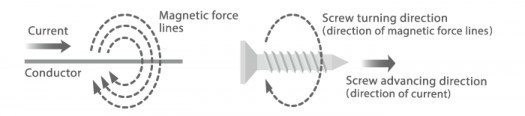
Hình 2.0-18: Xác định chiều đường sức từ trong dây thẳng
Khi dòng điện chạy trong một cuộn dây, các đường sức từ được kết hợp và cũng đi qua lõi của cuộn dây
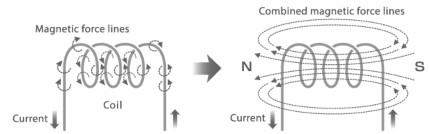
Hình 2. 0-19: Xác định chiều đường sức từ trong cuộn dây
Quy tắc ngón tay cái phải (Right hand thumb rule)
Quy tắc này giúp dễ hiểu hướng của các đường sức từ liên quan đến dòng điện.
Nếu ngón cái bàn tay phải chỉ chiều dòng điện chạy trong sợi dây thì 4 ngón còn lại cuốn cong lại quấn quanh sợi dây chỉ chiều của đường sức từ
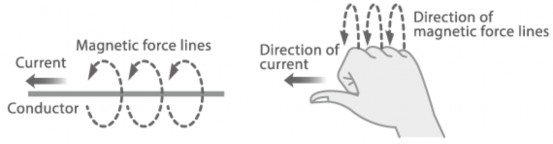
Hình 2.0-20: dòng diện chạy trong dây dẫn thẳng dài
Ngược lại nếu 4 ngón bàn tay phải nắm theo hướng dòng điên chạy trong lõi cuộn dây thì chiều của ngón cái choãi ra chỉ chiều của đường sức từ
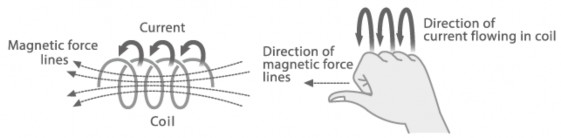
Hình 2. 0-21: dòng diện chạy trong cuộn dây dẫn
Ký hiệu cuộn cảm trong sơ đồ (schematic symbol for a inductor)
Ký hiệu của cuộn cảm là của một cuộn dây, do đó một cuộn dây cũng có thể được gọi là Cuộn cảm. Cuộn cảm thường được phân loại theo loại lõi bên trong chúng được quấn xung quanh.
Ví dụ : lõi rỗng (lõi không khí), lõi sắt rắn hoặc lõi ferit mềm với các loại lõi khác nhau được phân biệt bằng cách thêm các đường song song liên tục hoặc chấm chấm bên cạnh cuộn dây.
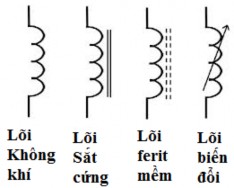
Hình 2. 0-22: Ký hiệu các loại cuộn cảm
Cuộn cảm gây ra một cảm kháng chống lại tốc độ biến thiên của dòng điện chạy qua nó. Do sự tích tụ năng lượng từ trường tự cảm ứng của nó, nó sẽ dễ dàng cho dòng một chiều DC đi qua. Khả năng chống lại các thay đổi trong dòng điện và từ thông của một cuộn cảm được gọi là hệ số tự cảm (Inductance) được ký hiệu L với đơn vị là Henry (H). Đơn vị Henry được đặt theo tên của Joseph Henry (1797-1878) nhà vật lý học người Mỹ. Ông là nhà khoa học đã phát hiện ra hiện tượng tự cảm vào năm 1832.
Bởi vì Henry là một đơn vị tương đối lớn về tự cảm theo đúng nghĩa của nó, cho nên các đơn vị tự cảm nhỏ hơn của Henry thường được sử dụng
1mH = 1 milli-Henry = 1/1000 Henry = 10-3H .
1μH = 1 micro-Henries = 1 / 1.000.000 Henry = 10-6H 1nH = 1 nano-Henries = 1 / 1.000.000.000 Henry = 10-9H
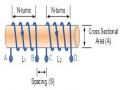
Một cuộn cảm diện tích lõi trung tâm (A) với chiều dài của số vòng dây liên tục của cuộn cảm là (l). Vì vậy, nếu một vòng dây được tạo bởi một từ thông Φ thì cuộn dây N vòng sẽ có thông lượng là NΦ.
Bất kỳ dòng (i) nào chảy qua cuộn dây sẽ tạo ra một dòng từ tính theo hướng ngược lại với dòng chảy của dòng điện. Sau đó, theo Luật của Faraday, bất kỳ thay đổi nào trong thông lượng từ này cũng tạo ra điện áp tự cảm ứng trong cuộn dây :
Ở đây:
o N là số vòng dây
o A là mặt cắt ngang ( m2)
o Φ là lượng thông lượng (Webers)
o μ là độ thấm của vật liệu làm lõi của cuộn dây
o l là chiều dài của cuộn dây (m)
o di / dt là tốc độ dòng thay đổi theo thời gian (A /s)
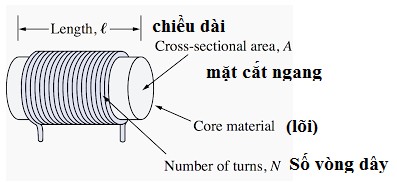
Hình 2. 0-23: cấu trúc của cuộn cảm
Mối quan hệ giữa thông lượng trong cuộn cảm và dòng điện chạy qua cuộn cảm được cho là: NΦ = Li.
Điện áp cảm ứng được tạo ra bởi cuộn cảm
VL = d/dt = dLi/dt = - Ldi/dt
Trong đó:
o L là tự cảm
o di / dt tốc độ thay đổi dòng điện.
Một điểm quan trọng cần lưu ý về phương trình trên
Nếu dòng điện dẫn là hằng số và không thay đổi như trong trạng thái ổn định của dòng DC, thì điện áp cảm ứng sẽ bằng 0 vì di / dt = 0.
Với dòng điện DC chảy qua cuộn cảm và do đó không gây ra điện áp trên nó, cuộn cảm hoạt động như một ngắn mạch bằng một sợi dây hoặc một điện trở giá trị rất thấp. Nói cách khác, sự ngăn cản dòng điện được cung cấp bởi một cuộn cảm là rất khác nhau giữa các mạch AC và DC.
Vấn đề (Problem)
Một dòng điện xác định 4 ampere đi qua một cuộn dây có độ tự cảm 0,5H. Xác định điện áp cảm ứng gây ra trong cuộn dây nếu công tắc được mở cho dòng điện chảy qua cuộn dây trong 10mS và sau đó dòng điện giảm xuống
không ampere.
Giải quyết vấn đề ( Solution)
Áp dụng công thức:
VL = Ldi/dt, thay giá trị L = 0.5H, Ii = 4, I2 = 0
=> di = 4 – 0 = 4 (A), dt = 0.01 (s)
Công suất cuộn cảm (Power in an Inductor)
Công suất tức thời được sử dụng để buộc dòng điện (i) chống lại điện áp cảm ứng (VL) được tính theo công thức
() [ ]
Năng lượng cuộn cảm (Energy stored by an Inductor)
Năng lượng thực sự được lưu trữ trong từ trường bao quanh cuộn cảm bởi dòng điện chạy qua nó
Trong đó: W là joules, L là Henries và I là Amperes
Trong một dòng điện xoay chiều, mạch AC một cuộn cảm liên tục lưu trữ và phân phối năng lượng trên mỗi chu kỳ.
Nếu dòng điện chạy qua cuộn cảm là hằng số như trong mạch DC, thì không có thay đổi về năng lượng được lưu trữ vì P = Li (di / dt) = 0.
Vì vậy, cuộn cảm có thể được định nghĩa là thành phần thụ động vì chúng có thể lưu trữ và cung cấp năng lượng cho mạch, nhưng chúng không tạo ra năng lượng.
2.3.2. Cảm kháng của cuộn dây
Trong mạch điện, khi một lực điện từ xuất hiện trong một mạch cảm ứng theo hướng mà chống lại bất kỳ sự thay đổi dòng điện nào trong mạch được gọi là Tự cảm ứng (L) nhưng đôi khi nó thường được gọi là suất điện động cảm ứng vì cực của nó theo hướng ngược lại với nguồn điện áp.
Hệ số tự cảm L thực sự là một thước đo của một cuộn cảm "kháng" với sự thay đổi của dòng điện chạy qua mạch
Đơn vị đo lường tự cảm cơ bản được gọi là Henry (H) nhưng nó cũng có đơn vị là Webers trên Ampere (1 H = 1 Wb / A).
( )
Trong đó: L là điện cảm trong Henries, VL là điện áp trên cuộn dây và di / dt là tốc độ thay đổi dòng điện trong Ampe trên giây, A / s.