c. Cả a và b đều đúng.
d. Cả a và b đều sai.
Câu 13:
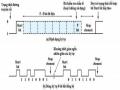
Đồng bộ theo hướng ký tự :
a. Không có start bit hay stop bit
b. Để thực hiện đồng bộ này, máy phát thêm vào các ký tự điều khiển truyền, gọi là các ký tự đồng bộ SYN, ngay trước các khối ký tự truyền.
c. a là phát biểu sai.
d. Cả a và b đều đúng.
Câu 14:
Lỗi định dạng frame có nghĩa là :
Có thể bạn quan tâm!
-
 Truyền Dẫn Đồng Bộ Và Bất Đồng Bộ
Truyền Dẫn Đồng Bộ Và Bất Đồng Bộ -
 Truyền Đồng Bộ Thiên Hướng Ký Tự
Truyền Đồng Bộ Thiên Hướng Ký Tự -
 Truyền số liệu - 15
Truyền số liệu - 15 -
 ?? X 8 X 7 X 5 X 3 X 1
?? X 8 X 7 X 5 X 3 X 1 -
 Truyền số liệu - 18
Truyền số liệu - 18 -
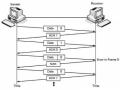
 Go - Back - N Arq (Truyền Lại Một Nhóm) Đặc Điểm
Go - Back - N Arq (Truyền Lại Một Nhóm) Đặc Điểm
Xem toàn bộ 210 trang tài liệu này.
a. Sau khi phát hiện đầu ký tự với một start bit, máy thu không phát hiện được số stop bit thích hợp.
b. Nghĩa là ký tự truyền không được nhận một cách hoàn hảo và cần phải truyền
lại.
c. Không phát hiện được start bit
d. a, b đều đúng.
Câu 15:
Trong kỹ thuật truyền dẫn nào, một start bit và stop bit để tạo frame ký tự:
a. Truyền dẫn bất đồng bộ
b. Truyền dẫn đồng bộ
c. Truyền dẫn song song
d. a và b
Câu 16:
Trong chế độ truyền không đồng bộ, thời gian trống (gap) giữa hai byte là:
a. Cố định
b. Thay đổi
c. Hàm theo tốc độ bit
d. Zero
Câu 17:
Truyền đồng bộ không cần thiết có:
a. Start bit
b. Stop bit
c. Khoảng trống giữa hai byte
d. Tất cả đều đúng
CHƯƠNG 5: ĐIỀU KHIỂN LIÊN KẾT DỮ LIỆU
5.1. Phát hiện lỗi và sửa sai
Trong các hệ thống truyền dẫn số, lỗi xảy ra khi có một bit bị biến đổi giữa bên gửi và bên nhận.
Có 2 dạng lỗi: Lỗi một bit và lỗi nhiều bit (burst) còn gọi là lỗi cụm.
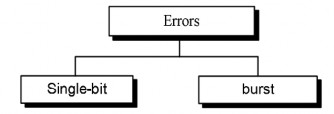
Hình 5. 1. Các dạng lỗi
- Lỗi một bit: Chỉ có một bit bị sai trong một đơn vị dữ liệu (byte, ký tự, đơn vị dữ liệu, hay gói)
Ví dụ: thay đổi từ 1 0 hoặc từ 0 1.
00000010 (STX: start of text) khi bị sai 1 bit dữ liệu nhận được 00001010 (LF: line feed)
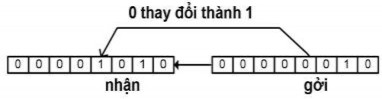
Hình 5. 2. Lỗi một bit
Lỗi một bit ít xuất hiện trong phương thức truyền nối tiếp, mà thường xuất hiện trong truyền song song.
- Lỗi cụm: có hai hoặc nhiều bit sai trong đơn vị dữ liệu.
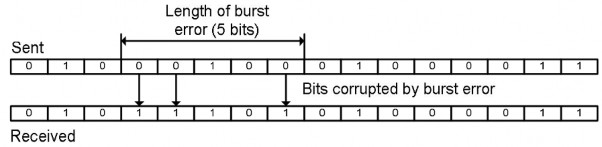
Hình 5.3. Lỗi nhiều bit (lỗi cụm)
Lỗi cụm không có nghĩa là các bit bị lỗi liên tục, chiều dài của bệt tính từ bit sai đầu tiên cho đến bit sai cuối. Một số bit bên trong cụm có thể không bị sai.
Lỗi cụm thường xuất hiện trong truyền nối tiếp.
Lỗi bit là không thể tránh khỏi trong quá trình truyền dẫn do nhiều nguyên nhân: đường truyền, lưu lượng truyền, loại mã đùng, loại điều chế, loại thiết bị phát, thiết bị thu, hay xuyên nhiễu và kết quả là một hoặc một số bit trong khung truyền bị lỗi. Để tăng xác suất thu đúng thông tin tại bên thu thì hệ thống cần sử dụng các biện pháp phát hiện và sửa sai tại đầu thu. Một số kỹ thuật thường được dùng:
- Dùng bộ giải mã có khả năng tự sửa sai
- Truyền lại một bộ phận của dữ liệu để thực hiện việc sửa sai, cách này gọi là ARQ - Automatic Repeat Request.
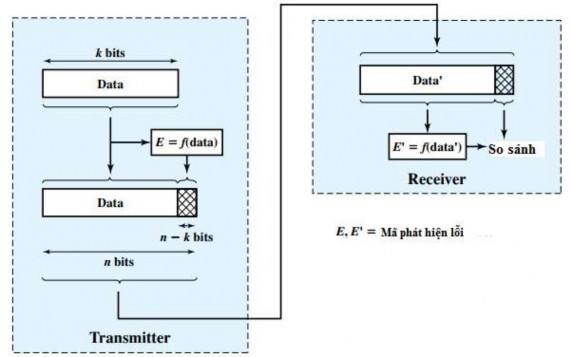
Hình 5.4. Xử lý phát hiện lỗi
Các phương pháp sửa lỗi đều dựa trên nguyên tắc sau: Khi một khung dữ liệu được truyền đi thì nó sẽ được chèn thêm một số bit kiểm tra gọi là mã phát hiện lỗi hay các bit kiểm tra. Mã này được tính toán như một hàm của các bit được truyền. Cụ thể, có một khối gồm k bit dữ liệu cần được truyền đi; từ khối bit này, người ta sử dụng một thuật toán phát hiện lỗi để tính ra mã phát hiện lỗi gồm (n – k) bit, với (n –
k) < k, để đóng gói cùng dữ liệu tạo thành một khung gồm n bit truyền đi. Bên thu tách khung thu được thành k bit dữ liệu và (n – k) các bit kiểm tra. Sau đó, dựa vào k bit thông tin thu được, bên thu sử dụng thuật toán phát hiện lỗi tương tự như bên phát để tính toán lại các bit kiểm tra; đối chiếu với các bit kiểm tra thu được. Nếu chúng khác nhau thì kết luận quá trình truyền tin có lỗi. Nguyên tắc trên được thể hiện như sơ đồ hình 5.4.
5.1.1. Phương pháp kiểm tra bit chẵn lẻ (parity bit)
Phương pháp thông dụng nhất được dùng để phát hiện lỗi của bit trong truyền không đồng bộ và truyền đồng bộ hướng ký tự là phương pháp kiểm tra bit chẵn lẻ (parity bit). Với cách này máy phát sẽ thêm vào mỗi ký tự truyền một bit kiểm tra parity đã được tính toán trước khi truyền. Khi nhận được thông tin truyền, máy thu sẽ thực hiện các thao tác tính toán trên các ký tự thu được, và so sánh với bit kiểm tra parity thu được. Nếu chúng bằng nhau, được giả sử là không có lỗi, ở đây ta dùng từ giả sử, bởi vì cách này có thể không phát hiện được lỗi trong khi lỗi vẫn tồn tại trong dữ liệu. Nhưng nếu chúng khác nhau thì chắc chắn một lỗi xảy ra.
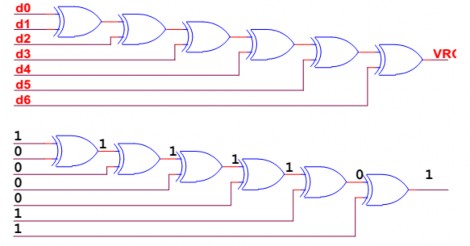
Hình 5.5. Mạch tạo bit kiểm tra chẵn (VRC) của một dữ liệu 7 bit: 1100001
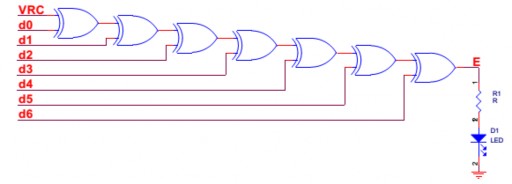
Hình 5.6. Mạch kiểm tra chẵn (VRC) của một dữ liệu 8 bit (11000011)
Để tính toán bit parity cho một ký tự, số các bit trong mã ký tự được cộng module 2 với nhau và bit parity được chọn sao cho tổng số các bit 1 bao gồm cả bit parity là chẵn (even parity) hoặc là lẻ (odd parity). Trong bộ mã ASCII mỗi ký tự có 7 bit và một bit kiểm tra.
Với kiểm tra chẵn giá trị của bit kiểm tra là 0 nếu số lượng các bit có giá trị 1 trong 7 bit là chẵn và có giá trị 1 trong trường hợp ngược lại.
Với kiểm tra lẻ thì ngược lại. Thông thường người ta sử dụng kiểm tra chẵn và bit kiểm tra gọi là P. Giá trị kiểm tra đó cho phép ở đầu thu phát hiện những sai sót
đơn giản.
Ví dụ 5.1:
Kí tự Mã ASCII Bit kiểm tra P Từ mã phát đi A 1000001 0 10000010
E 1010001 1 10100011
Phương pháp kiểm tra bit chẵn lẻ chỉ phát hiện các lỗi đơn bit (số lượng bit lỗi là số lẻ) và không thể phát hiện các lỗi 2 bit (hay số bit lỗi là một số chẵn)
5.1.2. Kiểm tra tổng BSC (Block Sum Check)
Khi các khối ký tự được truyền đi, xác suất một ký tự chứa lỗi bit gia tăng. Chúng ta có thể mở rộng các khả năng phát hiện lỗi từ một bit parity trên một ký tự (byte) bằng cách dùng một tập bit parity được tính từ toàn bộ khối ký tự trong khung. Với phương pháp này, mỗi ký tự trong khung được phân phối một bit parity như trên (parity hàng). Ngoài ra một bit mở rộng được tính cho mỗi vị trí bit (parity cột) trong toàn bộ khung. Tập các bit parity cho mỗi cột được gọi là ký tự kiểm tra khối, BCC (block check character) vì mỗi bit tạo nên ký tự này là tổng module 2 của tất cả các bit trong cột tương ứng. Ví dụ trong hình 5.7 dùng phương pháp kiểm tra lẻ cho các bit parity hàng, phương pháp kiểm tra chẵn cho các bit parity cột và giả sử khung chứa các ký tự in được.
a)
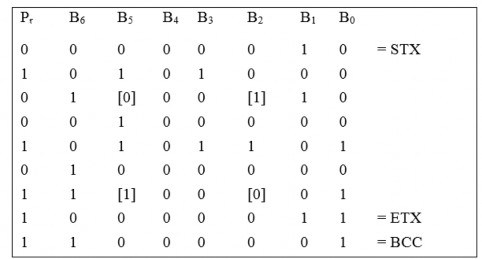
[ ] = ví dụ tổ hợp lỗi không phát hiện được Pr = Bit parity hàng
b)
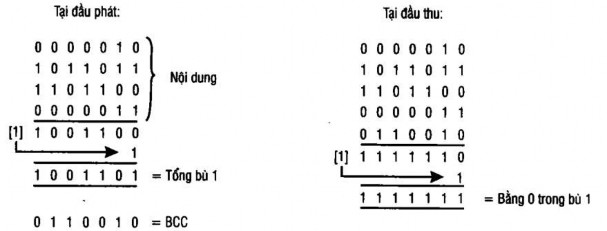
Hình 5.7. Ví dụ kiểm tra BSC: a) Các bit parity hàng và cột; b): Tổng bù 1 Trong ví dụ này thì, mặc dù các lỗi 2 bit trong một ký tự sẽ thoát khỏi kiểm tra
parity theo hàng, nhưng chúng sẽ bị phát hiện bởi kiểm tra parity cột tương ứng. Tuy nhiên, điều này chỉ đúng khi không có lỗi 2 bit xảy ra trong cùng một cột tại cùng thời điểm. Xác suất xảy ra trường hợp này nhỏ hơn nhiều so với xác suất xảy ra lỗi 2 bit trong một ký tự. Việc dùng kiểm tra tổng khối cải thiện đáng kể các đặc trưng phát hiện lỗi của lược đồ kiểm tra chẵn lẻ.
Một dạng khác của lược đồ trên dùng tổng bù 1 làm cơ sở cho kiểm tra tổng khối, thay vì dùng tổng module 2. Nguyên lý của lược đồ này minh họa trên hình 5.2 b.
Trong lược đồ này, các ký tự trong khối cần truyền được xem như các số nhị phân không dấu. Trước hết, các số này được cộng với nhau dùng phép toán bù 1. Tất cả các bit trong kết quả được đảo ngược bit (mã bù 1) và kết quả đảo ngược được dùng như ký tự kiểm tra khối BCC (mã bù 1). Tại máy thu, tổng bù 1 của tất cả các ký tự trong khối, bao gồm cả ký tự kiểm tra được tính. Nếu không có lỗi xuất hiện thì kết quả sẽ bằng zero. Với phép toán bù 1, số nhớ cuối được dùng, là bất kỳ giá trị nào vượt ra ngoài vị trí bit có nghĩa lớn nhất được cộng vào tổng nhị phân hiện hữu. Zero trong phép bù 1 được biểu diễn bởi tất cả các bit nhị phân đều là 0 hoặc tất cả đều là 1.
Từ hình 5.2 b, suy ra các đặc tính phát hiện lỗi của lược đồ này tốt hơn so với phương pháp tổng module 2. Tổng bù 1 được tính dễ dàng, nên được dùng như một phương pháp phát hiện lỗi trong một số ứng dụng yêu cầu hoạt động phát hiện lỗi chỉ được thực hiện bằng phần mềm.
Ví dụ 5.2:
Giả sử khối 16 bit sau được gửi đi dùng checksum 8 bit
10101001 00111001
Xác định các bit kiểm tra BCC và thực hiện việc kiểm tra khi bên thu thu đúng.
Giải:
Tính toán các bit BCC:
10101001
00111001
Tổng 11100010
BCC 00011101
Chuỗi bit truyền đi 10101001 00111001 00011101
BCC
Giả sử máy thu nhận được mẫu sau của ví dụ trên và không có lỗi, thì
10101001 00111001
Khi máy thu cộng ba phân đoạn lại:
10101001
00111001
00011101
Tổng 11111111 Kết quả không lỗi
5.1.3. Kiểm tra CRC (Cyclic Redundancy Check)
Các mã trên đây khá thích hợp cho các ứng dụng trong đó xuất hiện các lỗi đơn bit ngẫu nhiên. Tuy nhiên, khi các khối lỗi xuất hiện, chúng ta phải dùng một phương pháp chắc chắn hơn. Một trong những loại mã phát hiện lỗi phổ biến nhất hiện nay là mã vòng dư thừa CRC (Cyclic Redundancy Check).
Phương pháp kiểm tra tín hiệu bằng mã vòng được thực hiện như sau:
Cách 1:
Một từ mã được viết dưới dạng một đa thức
C(x) C
n1
X n1 C
n2
X n2 C X C
(5.1)
1
0
Tín hiệu cần phát đi trong khung gồm k bit sẽ được bên phát thêm vào (c = n-k) bit nữa để kiểm tra được gọi là Khung Check Sequence (FCS). Như vậy tín hiệu phát đi bao gồm n bit. Bên thu khi nhận được tín hiệu này sẽ đem chia cho một đa thức được gọi là đa thức sinh đã biết trước (bên phát và bên thu đều cùng chọn đa thức này). Nếu kết quả chia không dư coi như tín hiệu nhận được là đúng.
Kết quả dư lại của phép chia chính là CRC . Bên thu sau khi nhận được thông báo cũng đem chia cho hàm biết trước như bên phát. Nếu kết quả bằng 0 quá trình truyền không gây sai số.
Tính FCS gồm 4 bước:
+ Bước 1: Chuyển thông báo nhị phân thành đa thức M(x). Chọn hàm cho trước G(x) có bậc c, G(x) X c 1 ( c chính là độ dài của CRC )
+ Bước 2 : Nhân M (x) với X c
+ Bước 3 : Thực hiện phép tính
M (x) X c ta được phần nguyên và số dư
G(x)
Q(x) R(x) ,
G(x)
R(x) chính là CRC(FCS ) .
+ Bước 4 : Thành lập C(x) chính là thông báo cần truyền đi.
C(x) X c M (x) R(x)
Ví dụ: Tín hiệu cần truyền là 110101
Ta có M (x) X 5 X 4 X 2 1
Chọn đa thức sinh G(x) X 3 1, có c 3
Tính
M (x) X 3
G(x)
Q(x)
R(x)
G(x)
X3 + 1
X5 + X4 + X + 1
X8 + X7 + X5 + X3 X8 + X5
X7 + X3 X7 + X4
X4 + X
X3 +X X3 +1
X + 1
Vậy R(x) X 1; Q(x) X 5 X 4 X 1
G(x)
Thông tin cần truyền trên đường truyền là 110101011
Thu và kiểm tra CRC
Để kiểm tra sai số khi truyền, bộ phận thu đem khối thông tin thu được chia cho theo module 2 nếu phần dư còn lại là không mã nhận được là đúng, nếu phần dư
khác không mã nhận được là sai.
Kiểm tra CRC :
Ta có hàm phát đi: C(x) X c M (x) R(x)
Trong đó
X c M (x)
G(x)
Q(x)
R(x) ,
G(x)
R(x)
là đa thức dư
Tại đầu thu ta thu được C ' (x) đem giá trị thu được này chia cho đa thức sinh G(x)
ta có:
C ' (x) X c M (x) R(x) X c .M (x) R(x)
Q(x)
R(x) R(x)
G(x)
R(x)
G(x)
G(x)
G(x)
C ' (x)
G(x)
R(x)
= Q(x) (1 1)2
G(x)
mà (11)2 0 → G(x)
Q(x)