Phần dư bằng 0
Ví dụ 5.3:
Thông tin đã truyền đi là: 110101011
Thông tin nhận được là: 110101011. Thực hiện kiểm tra việc truyền tin không lỗi tại bên nhận.
Giải:
Kiểm tra việc truyền tin không lỗi tại bên nhận, điều này có nghĩa là truyền
đúng tức là R(x) phải bằng 0 .
Kiểm tra CRC như sau :
Chuyển thông tin nhận được thành đa thức :
1 1 0 1 0 1 0 1 1 → X 8 X 7 X 5 X 3 X 1
Đa thức sinh mà cả bên thu và bên phát đều đã biết G(x) X 3 1 đem đa thức
nhận được chia cho đa thúc G(x) chắc chắn phần dư sẽ bằng 0
Thực hiện phép chia như sau :
X3 + 1
X5 + X4 + X + 1
X8 + X7 + X5 + X3 + X + 1 X8 + X5
X7 + X3 X7 + X4
X4 + X3 + X X4+ X
X3 +1
X3 + 1
0 = R(x)
Cách 2:
Chúng ta có thể biểu diễn và xác định FCS trực tiếp từ các bit nhị phân theo cách dưới đây:
Chúng ta định nghĩa:
T = khung gồm n bit được truyền đi
D = khối dữ liệu gồm k bit, k bit ở vị trí đầu của T
F = mã kiểm tra FCS gồm (n – k) bit, (n-k) bit ở vị trí cuối của T P = mẫu gồm (n – k + 1) bit, đây là số chia được xác định trước Ta có thể biều diễn T như sau:
T = 2n-kD + F
F là chuỗi bit kiểm tra thêm vào sau các bit dữ liệu, và đảm bảo cho phép chia T/P không có dư.
Thực hiện phép chia 2n-kD/P, ta có:
Q
2nk D R P P
(5.2)
Trong đó Q là thương, R/P là phần dư. Vì phép chia module 2 nên phần dư luôn ít hơn số chia 1 bit. Chúng ta lấy phần dư này làm FCS.
Dưới đây, ta sẽ chứng minh R thỏa mãn điều kiện đảm bảo cho phép chia T/P không có dư. Thật vậy:
T 2nk D R
nk nk
T 2 D R 2 D R
(5.3)
P P P P
Thay biểu thức (5.2) vào (5.3), ta có:
T Q R R
(5.4)
P P P
Tuy nhiên, một số nhị phân khi cộng module 2 với chính nó thì bằng 0. Do đó:
T Q R R Q
(5.5)
P P
Như vậy, phép chia T/P không có dư, hay T chia hết cho P. Qua đó, ta thấy,
FCS dễ dàng được tạo ra bằng cách chia 2nk D cho P và sử dụng (n – k) bit phần dư
làm FCS. Bên thu sẽ thực hiện chia T cho P, nếu dư bằng 0 thì kết luận khung không lỗi.
Ví dụ 5.4:
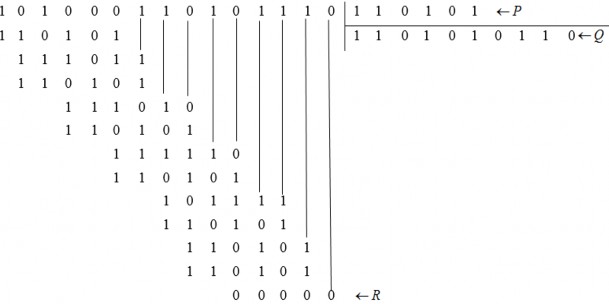
Cho bản tin cần truyền D = 1010001101 (10 bit) Mẫu P = 110101 (6 bit)
Xác định khung cần truyền?
Giải:
FCS cần xác định gồm 5 bit. Do đó, n = 15. Bản tin được nhân với 25 : 101000110100000. Ta thực hiện phép chia module 2: 25D cho P:

Phần dư được cộng với 25D tạo thành chuỗi bit T = 101000110101110 được truyền đi. Tại bên thu, chuỗi bit T nhận được sẽ được chia cho P để kiểm tra. Nếu không có lỗi xảy ra thì phần dữ sẽ bằng 0.
5.1.4. Phát hiện và sửa sai theo Hamming
Các phương pháp này được trình bày ở trên chỉ phát hiện lỗi truyền, không thể sửa sai. Phương pháp này được trình bày sau đây chỉ phát hiện lỗi sai mà còn có thể sửa sai cho một số bit nhất định.
Hình 5.8 mô tả tổng quát quá trình xử lý phát hiện lỗi. Khi dữ liệu được đọc vào trong bộ nhớ, việc tính toán biểu diễn bởi hàm f được tiến hành trên dữ liệu này để tạo ra một mã sửa sai. Cả mã và dữ liệu được lưu giữ. Do đó, nếu một M bit từ (word) được lưu giữ, và mã có chiều dài là k bit thì kích thước thực sự được lưu giữ là M + K bit.
Khi các từ được lưu giữ được đọc ra, mã được dùng để phát hiện và có sửa lỗi. Một tập mới của K bit đã được tạo ra từ M bit dữ liệu và được so sánh với các bit dữ liệu và được so sánh với các bit mã đã lưu giữ. Sự so sánh sẽ cho ra một trong ba trường hợp:
Tín hiệu báo lỗi
Dữ liệu ra
M
Dữ liệu vào M
M
K
Sửa lỗi
Bộ nhớ
f
So sánh
K
K
f
Hình 5.8. Chức năng sửa sai
1. Không có lỗi. Các bit giữ liệu được gửi ra.
2. Có lỗi, và có khả năng sửa được. Các bit dữ liệu và các bit sai được nạp vào một bộ sửa lỗi, nó tạo ra một tập M bit đã sửa được gửi ra.
3. Một lỗi nhưng không thể sửa được. Đây là điều kiện để gửi thông báo.
Một mã được đặc tính hoá bởi một số bit lỗi trong một từ mà nó có thể phát hiện lỗi và sửa sai. Các mã sửa sai đơn giản nhất là mã Hamming được phát minh bởi Richard Hamming tại Bell Laboratories..
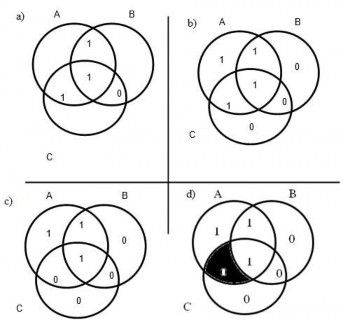
Hình 5.9. Cơ sở của mã sửa lỗi Hamming
Hình 5.9 dùng lược đồ Venn để mô tả việc dùng mã này trên các từ 4 bit (M = 4). Với 3 vòng tròn giao nhau có 7 ngăn, gán 4 bit dữ liệu vào các ngăn trong, hình 5.9
a. Các ngăn còn lại được làm đầy với parity (bit kiểm tra chẵn lẻ). Mỗi bit parity được chọn sao cho tổng số bit 1 trong các vòng tròn là chẵn (hình 5.9 b). Do đó, vì vòng A bao gồm 3 bit dữ liệu 1, nếu bit parity là 1. Bây giờ, nếu một lỗi xảy ra thay đổi một trong các bit này (hình 5.9 c), sẽ dễ dàng nhận ra. Bằng cách kiểm tra các bit parity sẽ thấy sự trái ngược trong vòng tròn A và C. Chỉ một trong 7 ngăn vừa thuộc A vừa thuộc C nhưng không thuộc B. Sau đó có thể sửa lại bit trong ngăn này
Để sáng tỏ hơn khái niệm này, tiếp theo có thể phát triển một mã có thể phát hiện và sửa sai các lỗi đơn trong các từ 8 bit. Khởi đầu cần xác định mã sẽ dài bao nhiêu. Xem hình 5.3, logic so sánh nhận hai giá trị K bit. Sự so sánh bit với bit được thực hiện bằng cách cộng module (xor) 2 ngò nhập. Kết quả được gọi là syndrome. Do đó phải mỗi bit của syndrome là 0 hay 1 tuỳ vào sự giống hay khác nhau của vị trí bit của trong 2 ngò nhập.
Từ syndrome có chiều dài K bit và có giá trị trong dải từ 0 đến (2k -1). Giá trị 0
cho biết không có lỗi .Vì một lỗi có thể xảy ra trên bất kỳ M bit dữ liệu hay K bit kiểm tra nào, nên phải có: 2k-1>=M+K
Bất đẳng thức này cho biết số bit cần thiết để sửa sai một bit bị sai trong một từ có M bit. Bảng 5.1 liệt kê số bit kiểm tra cần đối với chiều dài từ thay đổi. Từ bảng này, ta có thể thấy với từ 8 bit cần 4 bit cần 4 bit để kiểm tra. Để tiện dụng, Syndrom 4 bit với các đặc tính sau:
Nếu Syndrom chứa tất cả các bit 0, thì không có lỗi.
Nếu Syndrom chứa một và chỉ một bit đặt là 1 thì một lỗi xảy ra đối với một trong 4 bit kiểm tra. Không cần phải sửa.
Nếu Syndrom chứa nhiều hơn một bit 1 thì giá trị của sydrom chỉ vị trí của bit dữ liệu bị lỗi. Để sửa, bit dữ liệu này được đổi thành bit ngược lại.
Bảng 5.1. Gia tăng chiều dài từ với sửa lỗi.
Số bit dữ liệu | Số bit kiểm tra | %gia tăng | Số bit kiểm tra | %gia tăng |
8 | 4 | 50 | 5 | 62,5 |
16 | 5 | 31,25 | 6 | 37,5 |
64 | 6 | 18,75 | 7 | 21,875 |
128 | 7 | 10,94 | 8 | 12,5 |
256 | 8 | 6,25 | 9 | 7,03 |
5 | 9 | 3,52 | 10 | 3,9 |
Có thể bạn quan tâm!
-
 Truyền Đồng Bộ Thiên Hướng Ký Tự
Truyền Đồng Bộ Thiên Hướng Ký Tự -
 Truyền số liệu - 15
Truyền số liệu - 15 -
 Điều Khiển Liên Kết Dữ Liệu
Điều Khiển Liên Kết Dữ Liệu -
 Truyền số liệu - 18
Truyền số liệu - 18 -
 Go - Back - N Arq (Truyền Lại Một Nhóm) Đặc Điểm
Go - Back - N Arq (Truyền Lại Một Nhóm) Đặc Điểm -
 Lặp Lại Có Lựa Chọn (Selective - Repeat Arq)
Lặp Lại Có Lựa Chọn (Selective - Repeat Arq)
Xem toàn bộ 210 trang tài liệu này.
Các bit kiểm tra được tính toán như sau: C1 =M1 M2 M4 M5 M7 C2 =M1 M3 M4 M6 M7 C4 =M2 M3 M4 M8
C8 =M5 M6 M7 M8
Mỗi bit kiểm tra tính toán trên mối vị trí bit dữ liệu có số 1 nằm trong cột tương ứng. Do đó các vị trí 3,5,7,9 và 11 chứa 20, vị trí bit 3,6,7,10 và 11 chứa 21, vị trí bit 5, 6, 7, 12 chứa 22 và vị trí bit 9,10,11,12 chứa vị trí 23. Tổng quát, vị trí bit n được kiểm tra bởi các bit Ci sao cho i n Ví dụ, vị trí 7 được kiểm tra bởi các bit 4 và 1; và 7 = 4+2+1.
Ví dụ 5.5 :
Cho chuỗi bit dữ liệu là 0 0 1 1 1 0 0 1, và nếu vị trí bit 3 từ phải qua bị sai (thay vì 0 lại là 1) thì khi các bit kiểm tra mới được so sánh với các bit kiểm tra cũ, một từ Syndrom được hình thành:
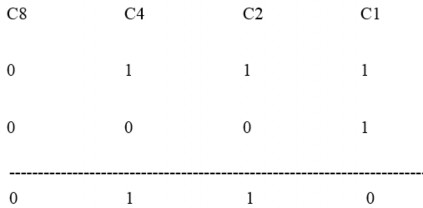
Kết quả này chỉ vị trí bit 6 từ vị trí bit 6 tử trái qua bị sai.
Ví dụ 5.6:
Cho chuỗi bit dữ liệu 01100101 được mã hóa theo mã sửa lỗi Hamming với các bit kiểm tra được tính toán như sau:
C1 =M1 M2 M4 M5 M7 C2 =M1 M3 M4 M6 M7 C4 =M2 M3 M4 M8
C8 =M5 M6 M7 M8
Giả sử chuỗi bit dữ liệu trên khi truyền đi bị lỗi ở vị trí thứ 3 tính từ bit có trọng số lớn nhất MSB. Hãy sử dụng phương pháp phát hiện và sửa sai Hamming để sửa lỗi này?
Giải:
Giả sử chuỗi bit dữ liệu trên khi truyền đi bị lỗi ở vị trí thứ 3 tính từ bit có trọng số lớn nhất MSB nên dữ liệu thu được là: 01000101
11 | 10 | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 | ||
Bit dữ liệu | M8 | M7 | M6 | M5 | M4 | M3 | M2 | M1 | ||||
Bit kiểm tra | C8 | C4 | C2 | C1 | ||||||||
1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | C80 | ||||
1 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | C41 | ||||
0 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | C20 | ||||
0 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | C10 | ||||
Từ được lưu | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 1 | ||||
Từ thu được | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 1 | ||||
1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | C81 | ||||
1 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | C41 | ||||
0 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | C21 | ||||
0 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | C10 | ||||
So sánh bit kiểm tra cũ với bit kiểm tra mới | ||||||||||||
Vị trí bit
C4 | C2 | C1 | |
0 | 1 | 0 | 0 |
1 | 1 | 1 | 0 |
1 | 0 | 1 | 0 |
Kết quả có giá trị bằng 10 vậy vị trí bit thứ 10 bị sai, thực hiện sửa vị trí thứ 6 là bit 0 thành bit 1. Vậy chuỗi dữ liệu thu đúng phải là : 01100101.
5.2. Nén dữ liệu
Chúng ta vẫn giả thiết rằng nội dung thông tin truyền đi bao gồm dữ liệu gốc dưới dạng chuỗi ký tự có chiều dầi cố định. Cho dù đây là trường hợp của nhiều ứng dụng truyền số liệu, vẫn còn có những trường hợp khác, trong đó dữ liệu được nén trước khi truyền đi, nén dữ liệu là một việc làm thiết yếu trong các dịch vụ truyền dẫn công cộng, ví dụ truyền qua mạng PSTN, vì trong các mạng các mạng như vậy việc tính cước dựa vào thời gian và cự ly truyền.
Ví dụ chúng ta truyền dữ liệu qua mạng PSTN dùng tốc độ 4800 bps, thời gian truyền hết dữ liệu là 20 phút. Rò ràng nếu dùng nén dữ liệu chúng ta có thể giảm một nửa số lượng dữ liệu truyền, và có thể tiết kiệm 50% giá tiền. Điều này tương đương với việc dùng tốc độ truyền 9600 bps nhưng không nén.
Trong thực tế chúng ta có thể dùng một loạt các giải thuật nén khác nhau, mỗi giải thuật sẽ phù hợp với một loại dữ liệu. Vài modem thông minh sẽ cung cấp đặc trưng nén thích nghi tự động thực hiện các giải thuật nén phù hợp với loại dữ liệu đang được truyền
5.2.1. Nén nhờ đơn giản mã cho các chữ số
Khi các khung chỉ bao gồm các ký tự số học đang được truyền, chúng ta có thể tiết kiệm đáng kể bằng cách giảm số bit trên mỗi ký tự từ 7 xuống 4 thông qua mã BCD, thay cho mã ASCII.
5.2.2. Nén theo mã hoá quan hệ
Một phương pháp khác được sử dụng khi truyền dữ liệu số học kế tiếp chỉ khác nhau phần nhỏ về giá trị là chỉ gửi lượng khác nhau giữa các giá trị này cùng với một giá trị tham khảo. Điều này được gọi là mã hóa quan hệ và nó có thể đem lại hiệu quả đặc biệt trong các ứng dụng ghi nhân dữ liệu.
Ví dụ nếu giám sát từ xa mực nước của dòng sông thường đọc mức nước theo các khoảng thời gian định trước. Để tối thiểu thời gian cần truyền thay vì truyền giá trị chỉ mức nước tuyệt đối, chúng ta chỉ cần truyền đi các giá trị khác nhau.
5.2.3. Nén bằng cách bỏ bớt các ký tự giống nhau
Thông thường khi các khung gồm các ký tự có thể in đang được truyền thường xuất hiện chuỗi lặp lại các ký tự giống nhau. Thiết bị điều khiển tại máy phát sẽ quét nội dung của khung trước khi truyền nếu gặp một chuỗi ký tự liên tiếp giống nhau thì chúng sẽ được thay thế bởi tuần tự số và ký tự.
5.2.4. Nén theo mã hoá Huffman
Phương pháp nén theo mã Huffman khai thác một đặc tính là không phải tất cả các ký hiệu trong một khung có cùng tần suất xuất hiện, ví dụ trong một khung bao gồm một chuỗi ký tự ,vài ký tự nào đó xuất hiện nhiều hơn các ký tự khác. Thay vì dùng một số bit nhất định trên một ký tự, chúng ta dùng một lược đồ mã hoá khác trong đó các ký tự xuất hiện thường xuyên được mã hoá với số bit ít hơn các ký tự có tần số xuất hiện thấp. Do đó lược đồ này là dạng mã hoá thống kê.
Trước hết, chuỗi ký tự truyền đợc phân tích và các loại ký tự và tần suất xuất hiện đợc xác định. Hoạt động mã hoá sau đó liên quan đến việc tạo ra một cây không cân bằng trong đó một số nhanh (là các mã trong thực tế) ngắn hơn một số nhánh khác. Mức độ thiếu cân bằng là một ham của tần suất xuất hiện các ký tự, càng đợc trải rộng ra độ mất cân bằng trong cây càng lớn. Kết quả cuối cùng một cây được gọi là cây Huffman.