Truyền số liệu

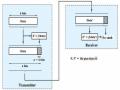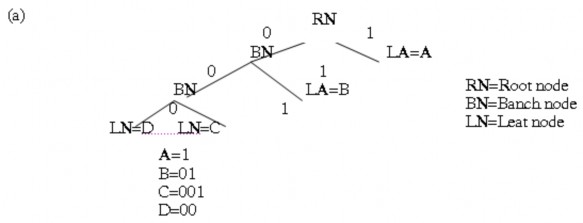
Hình 5.10. Cấu trúc cây mã Huffman

a) Cây sau cùng với các mã; b) Sự dẫn xuất cây.

Một cây Huffman là một cây nhị phân với các nhánh được gắn giá trị 0 hay 1. Xuất phát của cây thường là một đỉnh (hình học), trong thực tế được gọi là node gốc(root node), và một điểm tại đó một nhánh được rẽ ra coi như node nhánh (branch node). Điểm kết thúc của một nhánh gọi là node lá (leaf node), là các vị trí được gán cho các ký hiệu đang được mã hoá. Một ví dụ về Huffman được trình bày hình 5.9(a). Cây này tương ứng với các ký tự AAAABBCD.

Khi mỗi nhánh chia ra, một giá trị nhị phân 0 hay 1 được gán cho mỗi nhánh mới: một giá trị nhi phân 0 cho nhánh trái và một giá trị nhị phân 1 cho nhánh phải. Mỗi từ mã được dùng cho mỗi ký tự (được ghi tại các node lá) được xác định bằng cách dò theo đờn dẫn từ node gốc đến node lá tương ứng và hình thành một chuỗi các

giá trị nhị phân nằm trên đường dẫn. Từ các mã này chúng ta có thể suy ra sẽ dùng: 4x1 + 2x2 + 1x3 + 1x3 = 14 bit để truyền chuỗi hoàn chỉnh AAAABBCD.

Chúng ta cũng có thể suy ra lượng bit trung bình trên mỗi từ mã bằng lấy lượng bit trong mỗi từ mã nhận với xác suất xuất hiện rồi cộng toàn bộ lại. Cụ thể là :

Có thể bạn quan tâm!

Xem toàn bộ 210 trang tài liệu này.

1x0,5 + 2x0,25 + 3x0,125 + 3x0,125=1,75 bit/từ mã

Lượng bit trung bình tối thiểu trên một từ mã theo lý thuyết để truyền chuỗi thông điệp được gọi là entropy H, của thông điệp này. Có thể tính toán H bằng cách dùng công thức suy ra từ luật Shannon:

H Pi log 2 Pi bit/ từ mã (5.6)

i1

Trong đó n là số ký tự trong thông điệp và pi là xác suất xuất hiện của ký tự i trong thông điệp. Do đó thông điệp AAAABBCD, lượng bit trung bình tối thiểu trên một từ mã là :

H= - (0,5log 2 0,5 + 0,25log 2 0,25 +0,125 log 2 0,125 +0,125 log 2 0,125)=1,75 bit/ từ mã

Trong trường hợp này chúng ta có cùng kết quả khi dùng mã hoá Huffman.

Dùng từ mã ASCII 7-bit sẽ cần 8x7=56 bit đề truyền toàn chuỗi thông điệp này, con số này nhiều hơn đáng kể so với 14 bit khi dùng mã hoá Huffman.

Trong thực tế, điều này không phải là một so sánh chính xác vì với mã hoá Huffman, máy thu phải biết được tập ký tự biến đổi đang đợc truyền và các từ mã tương ứng, hay nói cách khác là cây Huffman. Một so sánh tốt hơn là xem sét số bit yêu cầu với mã hoá nhị phân thờng: bốn ký tự (A-D) cần hai bit cho mỗi ký tự, vậy cần truyền 8 ký tự. Rò ràng, lượng tiết kiệm không đang kể. Nhìn chung mã hoá Huffman là hiệu quả nhất khi các ký tự dang truyền có phân bố tần số rộng và các chuỗi ký tự dài. Ngược lại, nó không phù hợp cho truyền dữ liệu mã nhị phân của máy tính vì các byte 8 bit thờng xuất hiện với tần số như nhau.

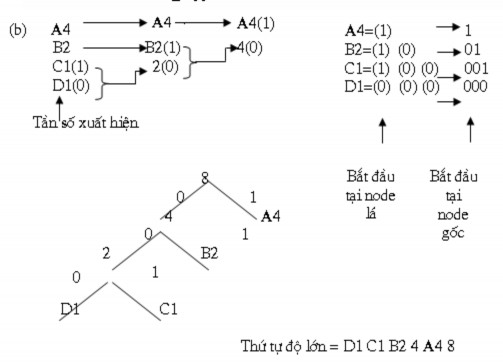
Để diễn tả làm thế nào xác định cây Huffman trong hình 5.10a, chúng ta phải dùng thêm thông tin liên quan đến tần số xuất hiện mỗi ký tự nh liệt kê trong hình 5.10b. Các ký tự được liệt kê trong một cột theo thứ tự giảm dần của tham số định lượng. Chúng ta có thể suy ra cây như sau:

Hai node lá đầu tiên phía dới danh sách C1 và D1 lần lượt được gán là nhánh 1 và nhánh 0 của một node nhánh. Sau đó hai node lá sẽ được thay thế bởi một node nhánh có định lượng bằng tổng hai node lá 2.1, cột mới được hình thành chứa node mới, sự kết hợp với các node còn lại từ cột đầu tiên, việc sắp xếp lại phải theo thứ tự định lượng giảm dần. Thủ tục này được lặp lại cho đến khi chỉ còn hai node.

Để suy ra từ mã kết quả cho mỗi ký tự chúng ta bắt đầu với ký tự trong cột đầu tiên và sau đo tiến hành liệt kê các số trong nhánh 0 hay 1 khi chúng gặp phải. Do đó

cho ký tự A số nhánh là 1 trong cột cuối cùng trong khi cho ký tự C nhánh đầu tiên là 1 sau đó là 0 tại node nhánh 2 và cuối cùng là 0 tại node nhánh 4. Tuy nhiên, các từ mã bắt đầu tại gốc chứ không phải tại node là vì các từ mã thực tế là ký tự ngược của các số này. Sau đó cây Huffman được xây dựng dễ dàng từ tập từ mã.

Chúng ta kiểm tra xem đây có phải là cây tối ưu và do đó là tập từ mã tối ưu hay không bằng cách liệt kê kết quả của tất cả các node nhánh và node là trong cây bắt đầu có định lượng nhỏ nhất và xử lý từ trái sang phải và từ đó lên trên các từ mã là tối ưu nếu danh sách kết quả ra tăng theo định lượng.

Ví dụ 5.7:

Một chuỗi thông điệp được truyền giữa hai máy tính PSTN. Các thông điệp bao gồm chỉ các ký tự từ A đến H. Phân tích cho thấy tần số xuất hiện của mỗi ký tự như sau: A và B = 0,25 C và D = 0,14 E,F,G and H =0,055

a) Dùng công thức Shannon để suy ra lượng bit trung bình tối thiểu trên một ký tự.

b) Dùng mã hoá Huffman để suy ra một tập từ mã và chứng minh tập này là tối ưu bằng cách xây dựng cây mã Huffman tương ứng.

c) Suy ra số bit trung bình trên một ký tự cho tập mã này và so sánh với:

(i) Giá trị Shannon

(ii) Các từ mã nhị phân có chiều dài cố đinh

(iii) Các từ mã ASCII 7 bit

Giải:

a) Theo công thức Shannon:

Entropy

H Pi log 2 Pi . Do đó: H = -(2(0,25 log 2 0,25) + 2(0,14 log 2 0,14) +

i1

4(0,055log 2 0,055))=1+0,794 + 0,921 = 2,715 bit/ từ mã

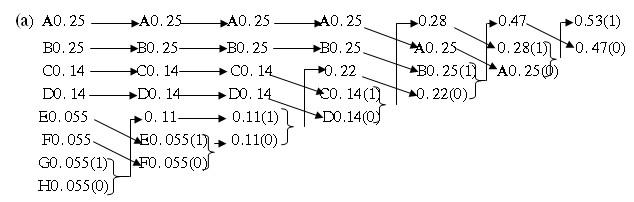
b) Việc suy ra bộ từ mã dùng mã hoá Huffman được trình bày trên hình 5.11 a. Trước hết các ký tự được liệt kê theo thứ tự trong số và hai ký tự dưới cùng của danh sách được gán nhanh (1) và (0). Tuy nhiên trong trường hợp này khi hai node kết hợp lại, trong số của node nhánh (0,11) lớn hơn trong số của hai ký tự E và F (0,055). Từ đó node nhánh này được chèn vào danh sách thứ hai có thứ tự cao hơn cả E và F. Thủ tục tương tự được lặp lại cho đến khi danh sách chỉ còn lại một node thì dừng.

Cây Huffman tương ứng với tập mã được suy ra được biểu diễn trên hình 5.6 b, và đây là cây tối ưu vì tất cả các node nhánh và node lá đều gia tăng theo thứ tự số học.

c) Số bit trung bình trong một từ mã dùng Huffman là:

2 (2 x 0,25) + 2 ( 3 x 0,14) + 4 (4 x 0,055) = 2,72 bit/ từ mã, bằng 99,8 % giá trị Shannon Dùng các từ mã nhị phân có chiều dài cố định:

Từ A đến H có 8 ký tự do đó có 3 bit trong mỗi từ mã, bằng 90,7 % giá trị Huffman:

(b)

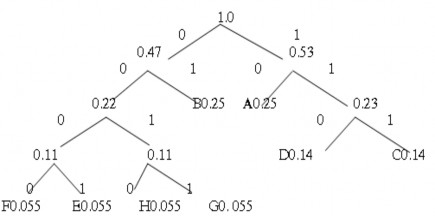
Hình 5.11. Ví dụ mã hoá Huffman:

a) Phát sinh từ mã; b) Cây mã Huffman. Dùng các từ mã ASCII 7 bit :

7 bit trong một từ mã, bằng 38,86 % giá trị Huffman.

Vì ký tự trong dạng mã hoá này có số bit thay đổi, nên luồng bit nhận được phải được dich ra theo từng bit thay vì dịch theo ranh giới 8 bit cố định. Do thứ tự các bit được gán trong quá trình mã hoá mà các từ mã Huffman có một đặc tính duy nhất là các từ mã ngắn hơn sẽ không bao giờ trùng với phần đầu của một từ mã dài hơn. Ví dụ nếu 011 là một từ mã hợp lệ thì không có một từ mã nào dài hơn chứa 011 kể từ bit đầu. Chúng ta có thể kiểm chứng điều này từ các mã được suy ra từ ví dụ trên.

Đặc tính này còn được gọi là đặc tính tiền tố (prefix), có nghĩa là luồng bit nhận được có thể bị giải mã một cách đơn giản bằng cách dò từng bit một cho đến khi tìm

thấy được từ mã hợp lệ. Một lưu đồ thuật toán giải mã thích hợp như hình 5.6. Giải thuật này giả sử ở máy thu đã có bảng mã và cũng giữ từ mã ASCII tương ứng.

5.3. Điều khiển luồng

5.3.1. Tổng quan

Nếu số lượng dữ liệu truyền giữa hai thiết bị là nhỏ, thiết bị phát có thể truyền tất cả dữ liệu ngay tức thời vì máy thu có đủ tài nguyên để tiếp nhận dữ liệu. Tuy nhiên, trong nhiều tình huống truyền tin điều kiện này không thể có. Do đó chúng ta phải dùng kỹ thuật để đảm bảo máy thu không bỏ qua bất kỳ phần tử dữ liệu nào do không đủ tài nguyên để lưu giữ. Điều này hết sứ quan trọng khi hai thiết bị đang truyền tin thông qua mạng số liệu, khi mà rất nhiều mạng sẽ đệm số liệu trong các bộ đệm có kích thước giới hạn. Nếu hai thiết bị hoạt động với tốc độ khác nhau, chúng ta thường phải điều khiển số liệu ngò ra của thiết bị tốc độ cao hơn để ngăn chặn trường hợp tắc nghẽn trên mạng. Điều khiển luồng thông tin giữa hai thiết bị truyền thường được gọi vắn tắt là điều khiển luồng (flow control).

Như vậy, điều khiển luồng là tập hợp các thủ tục để giới hạn lượng dữ liệu mà bên phát có thể gửi đi trước khi nhận được tín hiệu xác nhận ACK.

- Lưu lượng truyền này không được phép làm quá tải bên thu.

- Thiết bị thu thông báo cho bên gửi biết về các giới hạn dữ liệu và có thể yêu cầu gửi ít hơn hay tạm dừng truyền.

- Thiết bị thu còn có bước kiểm tra và xử lý dữ liệu trước khi sử dụng, điều này làm chậm đáng kể lưu lượng truyền dẫn, nên bên thu thường có thêm một khối nhớ tạm, thường được gọi là bộ nhớ đệm (buffer).

5.3.2. Các phương pháp điều khiển luồng

Có hai phương pháp được dùng là: dừng - và - chờ và cửa sổ trượt.

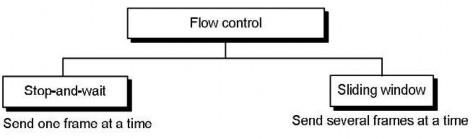
Hình 5.12. Hai phương pháp dùng trong điều khiển lưu lượng

5.3.2.1. Dừng - và - chờ (Stop - and - wait)

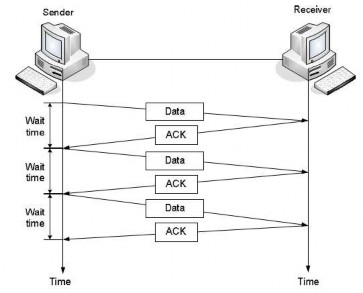
Hình 5.13. Phương pháp dừng - và - chờ

Trong phương pháp này, thiết bị phát gửi xong một khung và đợi tín hiệu xác nhận ACK rồi gửi tiếp khung kế.

Ưu điểm của phương pháp này là đơn giản.

Nhược điểm: tốc độ truyền bị chậm do quá trình dừng - và - chờ

5.3.2.2. Cửa sổ trượt (Sliding Window)

Phương pháp này cho phép nhiều khung cùng truyền một lúc.

Hình 5.14. Ghép nhiều khung thành một cửa sổ

Cửa sổ phát

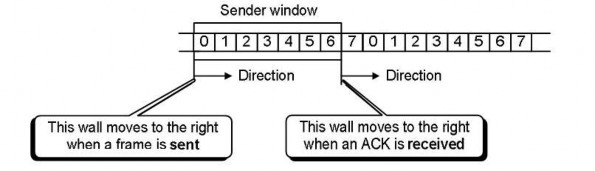
Hình 5.15. Cửa sổ phát

Dùng ý tưởng, cửa sổ trượt co từ bên trái khi khung dữ liệu được gửi đi. Cửa sổ trượt của thiết bị phát mở rộng về bên phải khi nhận được tín hiệu xác nhận ACK.

Cửa sổ thu:

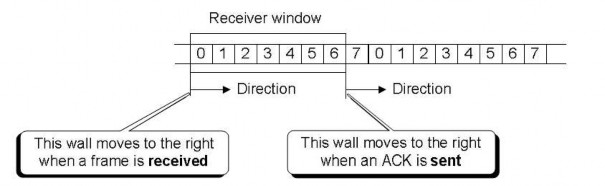
Hình 5.16. Cửa sổ thu

Dùng ý tưởng, cửa sổ trượt của máy thu co từ bên trái khi khung dữ liệu được nhận. Cửa sổ trượt của thiết bị thu mở rộng về bên phải khi gửi tín hiệu xác nhận ACK đi.

Ví dụ 5.8:

Khi mới bắt đầu, cửa sổ thiết bị phát và thu đều mở rộng tối đa bao gồm 7

khung.

Các khung này được đánh số từ 0 đến 7 và được lưu vào bộ đệm.

Bộ đệm phải có kích thước lớn hơn. Ví dụ trên bộ đệm có kích thước là 13. Kích thước của cửa sổ: kích thước của cửa sổ luôn nhỏ hơn chuỗi khung truyền

1 đơn vị để dễ thực hiện tín hiệu ACK. Giả sử số chuỗi khung là 8 và ta chọn kích thước cửa sổ cũng là 8. Nếu khung 0 được gửi và nhận tín hiệu ACK 1. Máy phát mở rộng cửa sổ và gửi các khung 1, 2, 3, 4, 5, 6, 7 và 0. Nếu lại nhận được ACK 1 thì không thể xác nhận được khi tín hiệu này là bản sao của ACK 1 trước đó (do mạng thực hiện) hay đó là ACK 1 mới khi mới nhận xong 8 khung. Nếu ta chọn kích thước cửa sổ là 7 thì điều nói trên không thể xảy ra.

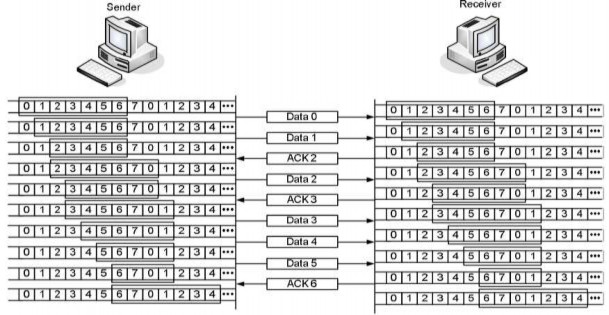
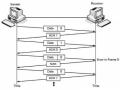
Hình 5.17. Quá trình truyền nhận dữ liệu dùng cửa sổ trượt

5.4. Kiểm soát lỗi

Kiểm soát lỗi là kỹ thuật nhằm phát hiện và sửa lỗi nếu khung truyền bị lỗi. Chúng ta sử dụng mô hình nghiên cứu cho các trường hợp được khái quát như mô tả trên hình 5.18. Dữ liệu được gửi đi dưới dạng một chuỗi các khung và các khung đến theo thứ tự. Số lượng các khung truyền đi không cố định. Có hai loại lỗi cơ bản trên đường truyền như sau:

- Mất khung: là trường hợp khung được gửi đi nhưng không đến đích (máy thu) theo yêu cầu.

- Lỗi khung: là trường hợp máy thu nhận được khung dữ liệu nhưng phát hiện ra một số bit trong khung bị lỗi.

Hầu hết các kỹ thuật điều khiển lỗi đều dựa trên một số hoặc tất cả các thành phần sau đây:

- Phát hiện lỗi: như đã tìm hiểu ở mục 5.1 và 5.2.

- ACK: Máy thu sẽ gửi lại gói tin báo nhận dương ACK để thông báo khung đã nhận thành công và không có lỗi.

- Truyền lại sau một khoảng thời gian chờ xác định (timeout): Máy phát sẽ tự động gửi khung dữ liệu nếu hết timeout mà không thấy có báo nhận ACK từ máy thu.

- NAK và truyền lại: Máy thu sẽ gửi lại một khung báo nhận âm NAK nếu nó phát hiện ra có lỗi khung. Máy phát sẽ phát lại khung bị thu lỗi đó.

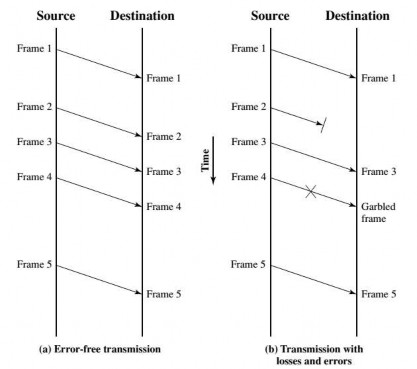
Hình 5.18. Mô hình truyền khung

Các kỹ thuật kiểm soát lỗi thường sử dụng cơ chế yêu cầu lặp lại tự động ARQ (automatic repeat request).