Cho chùm sao tín hiệu M-PSK, (|ℎ1|2+ |ℎ2|2− 1)|𝑥 𝑖|2, 𝑖 = 1,2, là hằng số cho tất cả các điểm tín hiệu đối với hệ số kênh truyền fading. Vì vậy, quy tắc quyết định trong (3.8) và (3.9) đơn giản như sau:
2
𝑥 1= arg min𝑥1∈𝑆 𝑑 (𝑥 1, 𝑥 1) (3.10)
𝑥 2= arg min 𝑑2(𝑥 2, 𝑥 2)
𝑥 2∈𝑆
3.2.1.3. Mô hình Alamouti với nhiều anten thu
Tx 1
h11
h12
h21
11 n12
r
H | |
Bộước lượng | |
Có thể bạn quan tâm!
-
Trường Hợp Csi Được Biết Tại Cả Phía Phát Và Phía Thu -
Kỹ Thuật Ghép Kênh Phân Chia Theo Tần Số Trực Giao. -
Tỷ Số Công Suất Đỉnh Trên Công Suất Trung Bình (Papr) -
Máy Thu V-Blast Zero-Forcing Toàn Bộ Giải Thuật Zf Triệt Tiêu Liên Tiếp Theo Thứ Tự Tối Ưu Như Sau: Khởi Động: -
Kỹ Thuật Partial Transmit Sequence (Pts) -
Giới Thiệu Phần Mềm Matlab Sử Dụng Để Mô Phỏng Hệ Thống Mimo
Xem toàn bộ 97 trang tài liệu này.
Bộkết hợp
Bộgiải mã ML
n
~
Space-T ime encoder c c * c c 1 2 1 2 c c * 2 1 | |
T | |
n n ~r
Bộkết hợp
Dữliệu
x
21 22
r
2 c
H | |
Bộước lượng | |
h 22
H
h M 1
h M 2
Bộkết hợp
r
n n
M 1 M 2
H | |
Bộước lượng |
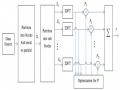
Hình 3.6. Sơ đồ Alamouti 2 anten phát và M anten thu
Mô hình Alamouti còn được ứng dụng vào hệ thống với hai anten phát và 𝑛𝑅
anten thu. Cách mã hóa và phát tín hiệu cho hệ thống này tương tự với trường hợp một
anten thu. Ký hiệu 𝑟𝑗 và 𝑟𝑗 tương ứng là tín hiệu thu tại anten thu thứ 𝑗 tại thời điểm 𝑡
và 𝑡 + 𝑇.
1 2
𝑟𝑗 = ℎ 𝑥 + ℎ 𝑥 + 𝑛𝑗 (3.11)
1 𝑗,1 1 𝑗,2 2 1
𝑟𝑗 = −ℎ 𝑥∗ + ℎ 𝑥∗ + 𝑛𝑗
2 𝑗,1 2 𝑗,2 1 2
Trong đó, ℎ𝑗,𝑖, 𝑖 = 1, 2, … , 𝑛𝑅, là hệ số fading trên đường truyền từ anten phát 𝑖
đến anten thu 𝑗, và 𝑛𝑗 và 𝑛𝑗 là tín hiệu nhiễu trên anten thu 𝑗 tại thời điểm 𝑡 và t + 𝑇
1 2
tương ứng.
Bộ thu xây dựng hai quyết định thống kê dựa trên việc kết hợp tuyến tính các tín hiệu thu. Quyết định thống kê ký hiệu là 𝑥 1 và 𝑥 2 cho như sau:
𝑥
= ∑𝑛𝑅 ℎ∗
𝑟𝑗 + ℎ
(𝑟𝑗)∗ = ∑2
∑𝑛𝑅 |ℎ
2
| 𝑥
+ ∑𝑛𝑅 ℎ∗
𝑛𝑗 + ℎ
(𝑛𝑗 )∗(3.12)
1 𝑗=1
𝑗,1 1
𝑗,2 2
𝑖=1
𝑗=1
𝑗,𝑖 1
𝑗=1
𝑗,1 1
𝑗,2 2
𝑥
= ∑𝑛𝑅 ℎ∗
𝑟𝑗 + ℎ
(𝑟𝑗)∗ = ∑2
∑𝑛𝑅 |ℎ
2
| 𝑥
+ ∑𝑛𝑅 ℎ∗
𝑛𝑗 + ℎ
(𝑛𝑗 )∗
1 𝑗=1
𝑗,2 1
𝑗,1 2
𝑖=1
𝑗=1
𝑗,𝑖 2
𝑗=1
𝑗,2 1
𝑗,1 2
Quy tắc giải mã của bộ tương quan lớn nhất cho hai tín hiệu x1 và x2 độc lập cho bởi công thức:
𝑥 = arg min
(∑𝑛𝑅|ℎ |2+ |ℎ |2− 1)|𝑥 |2+ 𝑑2(𝑥 , 𝑥
) (3.13)
1 𝑥 1∈𝑆
𝑗=1 1 2 1 1 1
𝑛𝑅
𝑥 2= arg min ( |ℎ1|2+ |ℎ2|2− 1) |𝑥 2|2+ 𝑑2(𝑥 2, 𝑥 2)
𝑥 2∈𝑆
𝑗=1
Đối với tín hiệu điều chế M-PSK, tất cả tín hiệu trong chùm sao có năng lượng bằng nhau. Luật giải mã tương quan lớn nhất tương đương với trường hợp một anten thu.
3.2.2. Bộ mã không gian thời gian STBC
3.2.2.1. Mã hóa không gian thời gian khối
Hình 3.7 mô tả cấu trúc mã hóa cho mã không gian thời gian khối. Tổng quát, ma trận phát 𝑋 kích thước 𝑛𝑇 × 𝑝 mô tả mã không gian thời gian khối. Trong đó 𝑛𝑇 là số anten phát, 𝑝 là số khoảng thời gian phát một khối của symbol mã hóa.
Giả sử rằng chùm sao tín hiệu mã hóa là 2𝑚 điểm. Tại mỗi thuật toán mã hóa, một khối gồm 𝑘𝑚 bit thông tin được ánh xạ thành chòm sao tín hiệu để chọn ra 𝑘 tín hiệu điều chế 𝑥1, 𝑥2, … , 𝑥𝑘 , trong đó mỗi nhóm 𝑚 bit chọn một tín hiệu trong chòm sao. Tín hiệu điều chế k được mã hóa bởi bộ mã hóa không gian thời gian khối để phát
𝑛𝑇 chuỗi tín hiệu song song có chiều dài 𝑝 qua ma trận phát 𝑋. Các chuỗi này được phát trên anten phát 𝑛𝑇 liên tục trong khoảng thời gian 𝑝.
Trong mã không gian thời gian khối, số symbol được mã hóa là 𝑘. Số khoảng thời gian phát yêu cầu phát symbol mã hóa qua nhiều anten phát là 𝑝. Mặt khác, có 𝑝 symbol không gian thời gian được phát từ mỗi anten cho mỗi khối gồm 𝑘 symbol. Tốc độ của mã không gian thời gian khối là tỷ số giữa số symbol đưa vào bộ mã hóa và số symbol không gian thời gian đã mã hóa phát trên mỗi anten cho bởi công thức:
𝑅 = 𝑘⁄𝑝
Information Source
Modulator
Space-time Block Encoder
X
Tx
𝑥1
𝑇𝑥𝑛𝑇
𝑥
𝑛𝑇
(3.14)
Hình 3.7. Mã hóa cho STBC
Hệ số phổ của mã không gian thời gian khối cho bởi công thức:
𝜂 =𝑟𝑏=𝑟𝑠𝑚𝑅= 𝑘𝑚
bit/s/Hz (3.15)
𝐵 𝑟𝑠 𝑝
Trong đó, 𝑟𝑏 và 𝑟𝑠 là tốc độ bit và tốc độ symbol tương ứng, và 𝐵 là băng thông. Ngõ vào của ma trận phát 𝑋 là sự kết hợp tuyến tính của 𝑘 symbol đã điều chế
𝑥1, 𝑥2, … , 𝑥𝑘 và liên hiệp phức của nó 𝑥∗, 𝑥∗, ⋯ , 𝑥∗ . Để thu được phân tập phát đầy đủ
1 2 𝑘
của 𝑛𝑇 , ma trận phát 𝑋 phải được xây dựng dựa trên thiết kế trực giao sau:
𝑇
𝑇
𝑋. 𝑋𝐻 = 𝑐(|𝑥1|2 + |𝑥2|2 + ⋯ + |𝑥𝑘 |2)𝐼𝑛 (3.16) Trong đó 𝑐 là hằng số, 𝑋𝐻 là Hermitian của 𝑋 và 𝐼𝑛 là ma trận đơn vị kích thước
𝑛𝑇 × 𝑛𝑇 . Hàng thứ 𝑖 của 𝑋 là symbol phát trên anten phát thứ 𝑖 liên tục trong khoảng thời gian phát 𝑝, trong khi cột thứ 𝑗 của ma trận 𝑋 là symbol phát trên anten nT tại thời điểm 𝑗. Thành phần của 𝑋 là hàng thứ 𝑖 và cột thứ 𝑗, 𝑥𝑖,𝑗, 𝑖 = 1, 2, … , 𝑛𝑇 , 𝑗 = 1, 2, … , 𝑝, biểu diễn tín hiệu phát từ anten 𝑖 tại thời điểm 𝑗.
Tốc độ mã không gian thời gian khối với phân tập phát đầy đủ nhỏ hơn hoặc bằng một, 𝑅 1. Mã với tốc độ 𝑅 = 1 yêu cầu không trải phổ, trong khi mã với tốc độ 𝑅 < 1 yêu cầu trải phổ 1/𝑅. Mã không gian thời gian khối với 𝑛𝑇 anten phát, ma trận truyền ký hiệu 𝑋𝑛𝑇 . Mã này được gọi là mã không gian thời gian khối với kích thước 𝑛𝑇 .
Chú ý thiết kế trực giao được ứng dụng vào việc tạo ra mã không gian thời gian
khối. Hàng của ma trận phát 𝑋𝑛𝑇 trực giao với nhau. Nghĩa là, trong mỗi khối, chuỗi tín hiệu từ hai anten phát trực giao. Ví dụ, nếu giả sử, 𝑥𝑖 = 𝑥𝑖,1, 𝑥𝑖,2, ⋯ , 𝑥𝑖,𝑝 là chuỗi phát từ anten thứ 𝑖 = 1, 2, … , 𝑛𝑇 , ta có:
𝑥 . 𝑥
= ∑𝑝
𝑥 . 𝑥∗ = 0 , 𝑖 𝑗, 𝑖, 𝑗 {1, 2, … , 𝑛
} (3.17)
𝑖 𝑗
𝑡=1
𝑖,𝑡 𝑗,𝑡 𝑇
Trong đó, 𝑥𝑖 . 𝑥𝑗 là tích của chuỗi của 𝑥𝑖 và 𝑥𝑗. Tính trực giao có thể thu được phân tập phát đầy đủ đối với số anten phát. Thêm nữa, nó cho phép bên thu nhận được hai tín hiệu phát từ các anten khác nhau và liên tục, giải mã đơn giản.
3.2.2.2. STBC cho chùm sao tín hiệu thực
Dựa vào dạng của chùm sao tín hiệu, mã không gian thời gian khối có thể phân loại thành mã không gian thời gian khối với tín hiệu thực và tín hiệu phức.
Tổng quát, nếu một ma trận phát 𝑋𝑛𝑇 thực kích thước 𝑛𝑇 × 𝑝 với biến
𝑥1, 𝑥2, … , 𝑥𝑘 thỏa mãn:
𝑋𝑛
. 𝑋𝑇 = 𝑐(|𝑥 |2 + |𝑥 |2 + ⋯ + |𝑥 |2)𝐼
(3.18)
𝑇 𝑛𝑇 1 2 𝑘 𝑛𝑇
Mã không gian thời gian khối có thể cung cấp phân tập phát đầy đủ 𝑛𝑇 với tốc độ mã 𝑘/𝑝.
Đơn giản hơn chúng ta có thể xem xét mã không gian thời gian khối với ma trận phát 𝑋𝑛𝑇 là ma trận vuông. Với bất kỳ chùm sao tín hiệu thực, điều chế M-ASK, mã không gian thời gian khối với ma trận vuông 𝑋𝑛𝑇 kích thước 𝑛𝑇 × 𝑛𝑇 tồn tại nếu và chỉ nếu số anten phát 𝑛𝑇 = 2, 4, hoặc 8. Ma trận truyền cho 𝑛𝑇 = 2 như sau:
𝑋2
𝑥1 −𝑥2
= [𝑥2 𝑥1 ] (3.19)
𝑛𝑇 = 4 | ||||
𝑥1 | −𝑥2 | −𝑥3 | −𝑥4 | |
𝑋 = 𝑥2 4 [𝑥3 | 𝑥1 −𝑥4 | 𝑥4 𝑥1 | −𝑥3 𝑥2 | |
𝑥4 | 𝑥3 | −𝑥2 | 𝑥1 | |
𝑛𝑇 = 8 | ||||
] (3.20)
𝑥1 −𝑥2
𝑥2 𝑥1
𝑥3 −𝑥4
𝑥4 𝑥3
𝑋8 =𝑥5 𝑥6
𝑥6 −𝑥5
𝑥7 −𝑥8
[𝑥8 𝑥7
−𝑥3 −𝑥4
𝑥4 −𝑥3
𝑥1 𝑥2
−𝑥2 𝑥1
𝑥7 𝑥8
𝑥8 −𝑥7
−𝑥5 𝑥6
−𝑥6 −𝑥5
−𝑥5 −𝑥6
𝑥6 𝑥5
𝑥7 −𝑥8
𝑥8 𝑥7
𝑥1 −𝑥2
𝑥2 𝑥1
𝑥3 −𝑥4
𝑥4 𝑥3
−𝑥7 −𝑥8
𝑥8 −𝑥7
𝑥5 𝑥6
−𝑥6 𝑥5
−𝑥3 −𝑥4
𝑥4 −𝑥3
𝑥1 𝑥2
−𝑥2 𝑥1]
(3.21)
Ma trận vuông có các hàng trực giao với ngõ vào ±𝑥1, ±𝑥2, … , ±𝑥𝑘. Từ các ma trận, quan sát một khối symbol đã điều chế 𝑘, cả hai số anten phát 𝑛𝑇 và số khoảng thời gian p yêu cầu phải bằng độ dài khối 𝑘. Ví dụ, với bốn anten phát, bộ mã hóa đưa vào 𝑘 = 4 symbol đã điều chế số thực 𝑥1, 𝑥2, 𝑥3, và 𝑥4. Tại thời điểm 𝑡 = 1, tín hiệu
𝑥1, 𝑥2, 𝑥3, và 𝑥4 phát trên các anten từ 1 đến 4 tương ứng. Tại thời điểm 𝑡 = 2, tín
hiệu phát trên các anten tương ứng là −𝑥2, 𝑥1, 𝑥2, −𝑥4 và 𝑥3, và tiếp tục. Ví dụ này cần bốn anten và bốn khoảng thời gian để phát bốn symbol. Vì vậy, mã này không yêu cầu trải băng thông.
Xây dựng được mô hình có tốc độ đầy đủ 𝑅 = 1 cho bất kỳ số anten phát. Tổng quát 𝑛𝑇 anten phát, khoảng thời gian phát p có giá trị nhỏ nhất cho bởi công thức sau:
min(24𝑐+𝑑) (3.22)
Trong đó:
𝑐, 𝑑|0 ≤ 𝑐, 0 ≤ 𝑑 ≤ 4, 𝑎𝑛𝑑 8𝑐 + 2𝑑 ≥ 𝑛𝑇 (3.23)
Với 𝑛𝑇 8, giá trị nhỏ nhất của p như sau:
𝑛𝑇 = 2, 𝑝 = 2
𝑛𝑇 = 3, 𝑝 = 4
𝑛𝑇 = 4, 𝑝 = 4
𝑛𝑇 = 5, 𝑝 = 8
𝑛𝑇 = 6, 𝑝 = 8
𝑛𝑇 = 7, 𝑝 = 8
𝑛𝑇 = 8, 𝑝 = 8 (3.24)
Qua những giá trị này, có thể tạo ma trận không vuông 𝑋3, 𝑋5, 𝑋6, và 𝑋7 dựa vào thiết kế trực giao số thực với kích thước 3, 5, 6, và 7 tương ứng. Các ma trận này như sau:
𝑥1 −𝑥2 −𝑥3 −𝑥4
𝑋3 = [𝑥2
𝑥3
𝑥1
−𝑥4
𝑥4
𝑥1
−𝑥3 ] (3.25)
𝑥2
𝑋5 =
𝑥1 −𝑥2
𝑥2 𝑥1
𝑥3 −𝑥4
𝑥4 𝑥3
−𝑥3 −𝑥4
𝑥4 −𝑥3
𝑥1 𝑥2
−𝑥2 𝑥1
−𝑥5 −𝑥6
𝑥6 𝑥5
𝑥7 −𝑥8
𝑥8 𝑥7
−𝑥7 −𝑥8
𝑥8 −𝑥7
𝑥5 𝑥6
−𝑥6 𝑥5
[𝑥5 𝑥6 𝑥7 𝑥8 𝑥1 −𝑥2 −𝑥3 −𝑥4 ]
𝑋6 =
𝑥1 −𝑥2
𝑥2 𝑥1
𝑥3 −𝑥4
𝑥4 𝑥3
−𝑥3 −𝑥4
𝑥4 −𝑥3
𝑥1 𝑥2
−𝑥2 𝑥1
−𝑥5 −𝑥6
𝑥6 𝑥5
𝑥7 −𝑥8
𝑥8 𝑥7
−𝑥7 −𝑥8
𝑥8 −𝑥7
𝑥5 𝑥6
−𝑥6 𝑥5
𝑥5 𝑥6 𝑥7 𝑥8 [𝑥6 −𝑥5 𝑥8 −𝑥7
𝑥1 −𝑥2 −𝑥3 −𝑥4
𝑥2 𝑥1 𝑥4 −𝑥3 ]
𝑥1 −𝑥2
𝑥2 𝑥1
𝑥3 −𝑥4
𝑋 =𝑥4 𝑥3
−𝑥3 −𝑥4
𝑥4 −𝑥3
𝑥1 𝑥2
−𝑥2 𝑥1
−𝑥5 −𝑥6
𝑥6 𝑥5
𝑥7 −𝑥8
𝑥8 𝑥7
−𝑥7 −𝑥8
𝑥8 −𝑥7
𝑥5 𝑥6
−𝑥6 𝑥5
7𝑥 𝑥 𝑥
𝑥 𝑥
−𝑥
−𝑥
−𝑥
5 6 7
8 1 2 3 4
𝑥6 −𝑥5 𝑥8 −𝑥7 [𝑥7 −𝑥8 −𝑥5 𝑥6
𝑥2 𝑥1 𝑥4 −𝑥3
𝑥3 −𝑥4 𝑥1 𝑥2 ]
Giải thích 𝑋6, ma trận mã không gian thời gian khối với sáu anten phát. Ngõ vào bộ mã hóa không gian thời gian khối là một block tám symbol 𝑥1, 𝑥2, …, 𝑥8 từ chòm sao điều chế. Sau khi mã hóa, symbol mã hóa phát trên sáu anten trong tám khoảng thời gian, anten thứ ba, tín 𝑥3, 𝑥4, 𝑥1, −𝑥2, −𝑥7, −𝑥8, 𝑥5 và 𝑥6 phát trên các anten từ một đến sáu.
3.3. Mã hóa không gian thời gian lưới STTC
3.3.1. Giới thiệu
STTC cho phép phân tập đầy đủ và có tốc độ mã cao. STTC là loại mã chập được mở rộng cho trường hợp MIMO. Cấu trúc mã chập đặc biệt phù hợp với truyền thông
vũ trụ và vệ tinh, do chỉ sử dụng bộ mã hóa đơn giản nhưng đạt được hiệu quả cao nhờ vào phương pháp giải mã phức tạp.
3.3.2 Cấu trúc mã hóa STTC
Trong STTC, bộ mã hóa ánh xạ dữ liệu nhị phân thành tín hiệu thành các symbol điều chế, với hàm điều chế được mô tả bằng sơ đồ lưới.
Xét bộ mã hóa không gian thời gian lưới điều chế M-PSK với 𝑛𝑇 anten phát như hình 3.8. Dòng ngõ vào, ký hiệu là 𝑐 cho như sau:
𝑐 = (𝑐0, 𝑐1, 𝑐2, ⋯ , 𝑐𝑡, ⋯ ) (3.26) Trong đó 𝑐𝑡 là nhóm 𝑚 = log2 𝑀 bit thông tin thời thời gian 𝑡
𝑐𝑡 = (𝑐1, 𝑐1, ⋯ , 𝑐𝑚) (3.27)
𝑡 𝑡 𝑡
Bộ mã hóa ánh xạ chuỗi tín hiệu vào thành chuỗi tín hiệu điều chế M-PSK
𝑥 = (𝑥0, 𝑥1, 𝑥2, ⋯ , 𝑥𝑡, ⋯ ) (3.28) Trong đó 𝑥𝑡 là symbol không gian thời gian tại thời điểm 𝑡
( 1 1
𝑛𝑇 𝑇
𝑥𝑡 =
𝑥𝑡 , 𝑥𝑡 , ⋯ , 𝑥𝑡 )
(3.29)
Tín hiệu điều chế, 𝑥1, 𝑥1, ⋯ , 𝑥𝑛𝑇 , được phát qua 𝑛
anten phát.
𝑡 𝑡 𝑡 𝑇
(𝑔1 … … 𝑔1 )
0,1
0,𝑛𝑇
(𝑔1 … … 𝑔1 )
1,1
1,𝑛𝑇
(𝑔1 … … 𝑔1
)
𝑐1
𝑣1,1
𝑣1,𝑛𝑇
𝑥1, 𝑥2, … . . 𝑥𝑛𝑇
𝑐𝑚
(𝑔𝑚 … … 𝑔𝑚
𝑣𝑚,1
𝑣𝑚,𝑛𝑇
)
(𝑔𝑚 … … 𝑔𝑚
1,1
1,𝑛𝑇
(𝑔𝑚 … … 𝑔𝑚 )
0,1
0,𝑛𝑇
Hình 3.8 Bộ mã hóa STTC
Bộ mã hóa như hình 3.8, chuỗi 𝑚 bit nhị phân đưa vào bộ mã hóa, gồm 𝑚 thanh ghi dịch. Chuỗi ngõ vào thứ 𝑐𝑘 = (𝑐𝑘, 𝑐𝑘, 𝑐𝑘, ⋯ , 𝑐𝑘, ⋯ ), 𝑘 = 1, 2, … 𝑚, đến thanh
0 1 2 𝑡
ghi dịch thứ 𝑘 và nhân với tập các hệ số mã hóa. Ngõ ra của bộ nhân từ tất cả các thanh ghi dịch và cộng modulo 𝑀, ngõ ra bộ mã hóa là 𝑥 = (𝑥1, 𝑥2, ⋯ , 𝑥𝑛𝑇 ). Các thành phần thanh ghi dịch và bộ cộng modulo 𝑀 được mô tả bởi các tập hệ số nhân 𝑚 như sau:
𝑔1 = [(𝑔1 , 𝑔1 , ⋯ , 𝑔1 ), (𝑔1 , 𝑔1 , ⋯ , 𝑔1 ), ⋯ , (𝑔1 , 𝑔1 , ⋯ , 𝑔1 )](3.30)
0,1
0,2
0,𝑛𝑇
1,1
1,2
1,𝑛𝑇
𝑣1,1
𝑣1,2
𝑣1,𝑛𝑇
𝑔2 = [(𝑔2 , 𝑔2 , ⋯ , 𝑔2 ), (𝑔2 , 𝑔2 , ⋯ , 𝑔2 ), ⋯ , (𝑔2 , 𝑔2 , ⋯ , 𝑔2 )]
0,1
⋮
0,2
0,𝑛𝑇
1,1
1,2
1,𝑛𝑇
𝑣2,1
𝑣2,2
𝑣2,𝑛𝑇
𝑔𝑚 = [(𝑔𝑚 , 𝑔𝑚 , ⋯ , 𝑔𝑚 ), (𝑔𝑚 , 𝑔𝑚 , ⋯ , 𝑔𝑚 ), ⋯ , (𝑔𝑚 , 𝑔𝑚 , ⋯ , 𝑔𝑚 )]
0,1
0,2
0,𝑛𝑇
1,1
1,2
1,𝑛𝑇
𝑣𝑚,1
𝑣𝑚,2
𝑣𝑚,𝑛𝑇
𝑗,𝑖
Trong đó, 𝑔𝑘 , 𝑘 = 1, 2, … , 𝑚, 𝑗 = 1, 2, … , 𝑣𝑘, 𝑖 = 1, 2, … , 𝑛𝑇 là các thành phần của chùm sao M-PSK, và 𝑣𝑘 là bộ nhớ của thanh ghi dịch thứ 𝑘.
𝑡
Ngõ ra của bộ mã của anten phát thứ 𝑖 ở thời điểm 𝑡, ký hiệu là 𝑥𝑖 tính toán như
sau:
𝑥𝑖 = ∑𝑚
∑𝑣𝑘
𝑔𝑘
𝑐𝑘 mod 𝑀, 𝑖 = 1,2, ⋯ , 𝑛
(3.31)
𝑡 𝑘=1
𝑗=0
𝑗,𝑖
𝑡−𝑗 𝑇
Những giá trị ngõ ra này là các thành phần của tập tín hiệu M-PSK. Dạng tín hiệu điều chế không gian thời gian phát tại thời điểm 𝑡
( 1 1
𝑛𝑇 𝑇
𝑥𝑡 =
𝑥𝑡 , 𝑥𝑡 , ⋯ , 𝑥𝑡 )
(3.32)
Mã không gian thời gian lưới M-PSK có hệ số băng thông 𝑚 bits/s/Hz. Tổng bộ nhớ của bộ mã hóa 𝑣
𝑣 = ∑
𝑚
𝑘=1
𝑣𝑘
(3.33)
Với 𝑣𝑘, 𝑘 = 1, 2, … , 𝑚, là bộ nhớ của nhánh mã hóa thứ 𝑘. Giá trị của 𝑣𝑘 cho chùm sao M-PSK tính như sau:
𝑣𝑘
= ⌊𝑣+𝑘−1⌋ (3.34)
log2 𝑀
Tổng số trạng thái của bộ mã hóa lưới là 2𝑣. Tập các hệ số nhân 𝑚 được gọi là chuỗi sinh.
Xét mã không gian thời gian lưới QPSK với hai anten phát. Bộ mã hóa bao gồm hai thanh ghi dịch. Cấu trúc bộ mã hóa cho mô hình với bộ nhớ 𝑣 như hình 3.9
Hai chuỗi nhị phân 𝑐1 = (𝑐1, 𝑐1, 𝑐1, ⋯ , 𝑐1, ⋯ ) và 𝑐2 = (𝑐2, 𝑐2, 𝑐2, ⋯ , 𝑐2, ⋯ ) đưa
0 1 2 𝑡 0 1 2 𝑡
vào các thanh ghi dịch mã hóa trên và dưới. Bộ nhớ của thanh ghi dịch trên và dưới tương ứng là v1 và v2 với v = v1 + v2. Hai chuỗi ngõ vào này được nhân với các hệ số:
𝑔1 = [(𝑔1 , 𝑔1 ), (𝑔1 , 𝑔1 ), ⋯ , (𝑔1 , 𝑔1 )] (3.35)
0,1
0,2
1,1
1,2
𝑣1,1
𝑣1,2
𝑔2 = [(𝑔2 , 𝑔2 ), (𝑔2 , 𝑔2 ), ⋯ , (𝑔2 , 𝑔2 )]
0,1
0,2
1,1
1,2
𝑣2,1
𝑣2,2
𝑗,𝑖
Trong đó 𝑔𝑘 ∈ {0,1,2,3} , 𝑘 = 1, 2; 𝑖 = 1, 2; 𝑗 = 0, 1, … , 𝑣𝑘. Ngõ ra của bộ nhân tiếp tục được cộng modulo 4 với nhau
𝑥𝑖 = ∑2
∑𝑣𝑘
𝑔𝑘
𝑐𝑘 mod 4, 𝑖 = 1,2 (3.36)
𝑡 𝑘=1
𝑗=0
𝑗,𝑖
𝑡−𝑗
Ngõ ra của bộ cộng là 𝑥1 và 𝑥2 là các điểm trong chòm sao QPSK. Sau đó phát
𝑡 𝑡
các điểm này trên hai anten thứ nhất và thứ hai tương ứng.
(𝑔1 , 𝑔1 )
0,1 0,2
(𝑔1 , 𝑔1 )
1,1 1,2
𝑐1
(𝑔1 ,1, 𝑔1 ,2)
𝑣1𝑣1
𝑡
(𝑥1, 𝑥2)
𝑡 𝑡
𝑐2
𝑡
(𝑔 , 𝑔 )
2 2
𝑣 ,1 𝑣 ,2
2 2
(𝑔2 , 𝑔2 )
1,1 1,2
(𝑔2 … … 𝑔2 )
0,1
0,2
Tín hiệu nhận được tại máy thu sẽ được bộ giải mã tương quan tối đa không gian thời gian STMLD (Space-Time Maximum Likelihood Decoder) giải mã. Bộ STMLD sẽ được thực hiện thành giải thuật vector Viterbi, đường mã nào có metric tích lũy nhỏ nhất sẽ được chọn là chuỗi dữ liệu được giải mã. Độ phức tạp của bộ giải mã tăng theo hàm mũ với số trạng thái trên giản đồ chòm sao và số trạng thái lưới, một bộ mã STTC có bậc phân tập là D truyền dữ liệu với tốc độ 𝑅 bps thì độ phức tạp của bộ giải mã tỷ lệ với hệ 2𝑅(𝐷−1).
Hình 3.9 Bộ mã hóa STTC với hai anten phát
STTC cung cấp độ lợi mã tốt hơn nhiều STBC độ lợi mã của STTC tăng lên khi tăng số trạng thái của lưới mã. Tuy nhiên độ phức tạp của STBC thấp hơn nhiều độ phức tạp của STTC, do STBC được mã hóa và giải mã đơn giản nhờ vào các giải thuật xử lý tuyến tính, nên STBC phù hợp với các ứng dụng thực tế trong hệ thống MIMO hơn.
3.4. Mã hóa không gian thời gian lớp BLAST
Sau khi khám phá ra khi các đường tán xạ đủ lớn, kênh truyền đa đường vô tuyến có khả năng cung cấp một dung lượng khá lớn nhờ vào các kiến trúc xử lý thích hợp. Năm 1996, G.J.Foshchisi thuộc phòng thí nghiệm Bell đã đưa ra các kiến trúc D- BLAST (Diagonal-Bell Laboratories Layered Space-Time) sử dụng đa anten phát và thu với kỹ thuật mã hóa phân lớp theo đường chéo, từng khối dữ liệu sẽ được truyền theo đường chéo. Trong môi trường tán xạ Rayleigh, kiến trúc này có thể cung cấp dung lượng tăng tuyến tính theo số anten phát và anten thu (với giả sử rằng số anten phát và thu là bằng nhau) và có thể đạt tời gần 90% dung lượng Shannon. Tuy nhiên