Giới Thiệu Phần Mềm Matlab Sử Dụng Để Mô Phỏng Hệ Thống Mimo

Yes

interleaver

IFFT

𝑃 < 𝑃

𝑖 𝑇

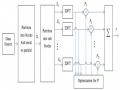
trước gọi là ngưỡng, các giá trị PAPR mới của chuỗi dữ liệu sau khi hoán vị sẽ được so sánh với mức ngưỡng này. Thuật toán hoán vị thích ứng sẽ được minh họa như hình 4.7.

Có thể bạn quan tâm!

Xem toàn bộ 97 trang tài liệu này.

Hình 4.7. Thực hiện hoán vị thích ứng

4.3. Giảm PAPR dùng phương pháp PTS

Kỹ thuật chuỗi phát từng phần PTS (Partail Transmit Sequence) chia một khối dữ liệu ngõ vào thành N symbol vào V khối con tách rời nhau như sau:

𝑋 = 𝑋0, 𝑋1, 𝑋2, … , 𝑋𝑉−1, 𝑇 (4.9)

𝑣=1

Với 𝑋𝑖là những khối con liên tiếp nhau và có kích thướcbằng nhau. Không giống như kỹ thuật SLM sự xáo trộn được áp dụng cho tất cả các sóng mang con, trong kỹ thuật PTS, sự xáo trộn (quay pha của nó một cách độc lập) được áp dụng cho từng khối con (hình 4.8). Sau đó mỗi sóng khối con được nhân với hệ số xoay pha tương ứng 𝑏𝑣= 𝑒𝑗𝜙𝑣 , 𝑣 = 1, 2, … , 𝑉, sau đó sẽ được đưa qua IFFT để biến đổi.

𝑣=1

𝑥 = 𝐼𝐹𝐹𝑇{∑𝑉

𝑏𝑣𝑋𝑣} = ∑𝑉

𝑏𝑣 𝑋𝑣 ∙ 𝐼𝐹𝐹𝑇{𝑋𝑣} = ∑𝑉

𝑏𝑣 𝑥𝑣

(4.10)

[𝑏̃1… 𝑏̃𝑣] = min

𝑏1…𝑏𝑣𝑛=0,1,…,𝑁−1

𝑣

max 𝑏𝑣. 𝑥𝑣𝑛

𝑣=1

Hình 4.8. Sơ đồ khối phương pháp PTS

Với 𝑥𝑣 là một PTS. Vector xoay pha được chọn sao cho PAPR là nhỏ nhất.

[𝑏̃1, … , 𝑏̃𝑉] = 𝑎𝑟𝑔 min[𝑏̃1,…,𝑏̃𝑉](max𝑛=0,1,…,𝑁−1|𝑏𝑣𝑥𝑣 𝑛 |) (4.11) Sau đó, ta có tín hiệu trên miền thời gian tương ứng với PAPR nhỏ nhất như sau:

𝑣=1

𝑥 = ∑𝑉

𝑏̃𝑣𝑥𝑣

(4.12)

𝑣=1

Tóm lại, việc lựa chọn các vector pha {𝑏𝑣 }𝑉 được giới hạn số phần tử nhằm làm giảm sự phức tạp khi tìm kiếm. Khi thiết lập các hệ số pha được cho phép

𝑏 = {𝑒𝑗2𝜋⁄𝑊|𝑖 = 0, 1, … , 𝑊 − 1}, 𝑊𝑉−1 hệ số pha cần được tìm để thiết lập tối ưu các hệ số pha. Do đo, độ phức tạp của tìm kiếm tăng theo cấp số nhân theo số lượng các khối con.

Kỹ thuật PTS đòi hỏi V IFFT thực hiện cho mỗi khối dữ liệu và ⌊log2 𝑊𝑉 ⌋ bit

thông tin. Đặc tính PAPR của PTS không chỉ bị ảnh hưởng bởi số lượng các khối con V và số lượng hệ số pha cho phép W mà còn sự phân chia các khối con. Thực tế, có ba loại sơ đồ phân chia khối con: liền kề, xen kẽ và giả ngẫu nhiên. Trong số đó, giả ngẫu nhiên có đặc tính tốt nhất.

Như đã nói ở trên, kỹ thuật PTS bị ảnh hưởng do sự phức tạp khi thiết lập tối ưu các hệ số pha, đặc biệt là khi số lượng khối con tăng lên. Một số sơ đồ khác có thể làm giảm sự phức tạp này. Một ví dụ cụ thể là thuật toán kết hợp tối ưu, sử dụng hệ số pha nhị phân {1, −1}. Được tóm tắt như sau:

1. Phân chia dữ liệu ngõ vào như trong phương trình (4.9).

2. Thiết lập tất cả các hệ số pha 𝑏𝑣 = 1 với 𝑣 = 1: 𝑉, tìm PAPR_min như phương trình (4.10).

3. Đặt 𝑣 = 2.

4. Tính PAPR theo phương trình (4.10) với 𝑏𝑣 = −1.

5. Nếu PAPR > PAPR_min, thay 𝑏𝑣 ngược lại 1. Nếu không thay PAPR_min = PAPR.

6. Nếu v<V, thì tăng v lên 1 và quay lại bước 4. Nếu không, thoát khỏi chương trình với hệ số pha tối ưu 𝑏̃.

Số phép tính trong phương trình (4.10) trong thuật toán kết hợp tối ưu là V, ít hơn nhiều so với phương pháp PTS gốc (𝑉 ≪ 𝑊𝑉).

CHƯƠNG V: MÔ PHỎNG HỆ THỐNG MIMO-OFDM & ĐÁNH GIÁ CHẤT LƯỢNG HỆ THỐNG

5.1. Giới thiệu phần mềm Matlab sử dụng để mô phỏng hệ thống MIMO

MATLAB là một bộ chương trình phần mềm lớn của lĩnh vực toán số. Tên bộ chương trình là chữ viết tắc từ Matrix Laboratory, thể hiện định hướng chính của chương trình là các phép tính vector và ma trận. Phần cốt lõi của chương trình bao gồm một số hàm toán, các chức năng nhập/xuất cũng như các khả năng điều khiển chu trình mà nhờ đó ta có thể dựng nên các Scripts.

Trong thực tế MATLAB còn ứng dụng rất rộng rãi trong nhiều lĩnh vực và nó cũng sử dụng rất nhiều các phép tính toán học. Với những đặc điểm đó và khả năng thân thiện với người sử dụng nên nó dễ dàng sử dụng hơn các ngôn ngữ khác như Basic, Pascal, C.

Nó cũng cấp một môi trường phong phú cho biểu diễn dữ liệu, và có khả năng mạnh mẽ về đồ hoạ, bạn có thể tạo các giao diện riêng cho người sử dụng (GUIs) để giải quyết những vấn đề riêng cho mình.

Với những khả năng mạnh mẽ, rộng lớn của MATLAB, tôi đã ứng dụng các tính năng của nó để mô phỏng tính toán các thông số liên quan đến hệ thống MIMO- OFDM.

Sau khi khởi động MATLAB ta thu được màn hình MATLAB, môi trường tích hợp với những cữa sổ chính như hình 5.1.

Hình 5.1 Giao diện làm việc chính của MATLAB

5.2. Giao diện chính của chương trình

Hình 5.2. Giao diện chính của chương trình

Chọn mô phỏng để bắt đầu chương trình

Hình 5.3. Chương trình mô phỏng

Chương trình gồm 3 vấn đề:

Phần 1: Gồm hai vấn đề chính như sau:

- Tính BER của hệ thống Alamouti

- Tính BER của hệ thống MIMO 4x4 Phần 2: Gồm hai vấn đề:

- Tính dung lượng của hệ thống khi thông tin kênh truyền chỉ được biết tại bên thu

- Tính dung lượng của hệ thống khi thông tin kênh truyền được biết tại cả bên phát và bên thu.

Phần 3: Mô phỏng phương pháp giảm PAPR của hệ thống OFDM dùng kỹ thuật PTS.

5.3. Tính BER của hệ thống MIMO – OFDM

5.3.1. Mô hình Alamouti

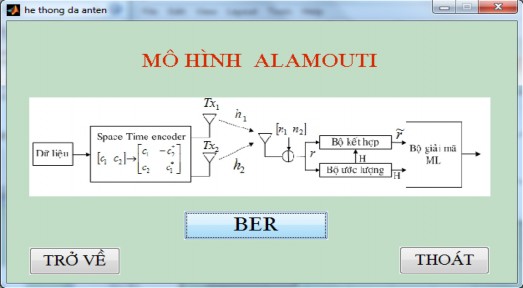
Hình 5.4. Giao diện tính BER của mô hình Alamout trong hệ thống MIMO – OFDM

Chọn BER để thực thi chương trình tính BER của hệ thống MIMO

Hình 5.4 mô tả BER của các hệ thống SISO (1x1), SIMO (1x2), MISO (2x1), MIMO (2x2) dùng mã hóa không gian-thời gian khối, mô hình Alamouti. Với các thông số:

- Chiều dài một khung là 100.

- Số lượng gói là 1000.

- Eb/No từ 0 đến 20.

- Mô hình kênh truyền fading và nhiễu Gauss.

- Điều chế dạng QPSK

Kết quả mô phỏng BER của hệ thống Alamouti

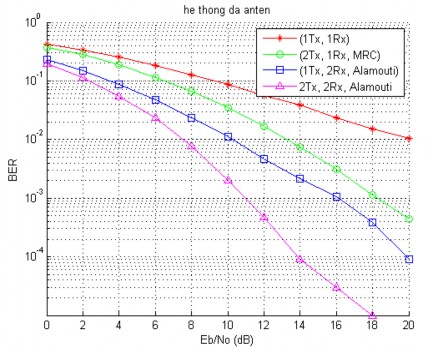
Hình 5.5. BER của mô hình Alamouti trong hệ thống MIMO

Nhận xét:

Quan sát hình 5.5 ta thấy BER của hệ thống tốt dần lên theo số lượng các anten. BER của hệ thống Alamouti tốt hơn hẳn so với hệ thống MIMO. Khi tăng số anten thu thì BER của sơ đồ Alamouti giảm theo. Trong khi đó, công suất phát trên mỗi anten của sơ đồ Alamouti chỉ bằng một nửa so với SISO hay SIMO. Việc giảm công suất phát sẽ dẫn đến việc giảm giá thành của bộ khuếch đại công suất giúp giảm chi phí sẽ làm tăng hiệu quả sử dụng.

BER của hệ thống Alamouti 2x1 cao hơn so với hệ thống MRC 1x2 do công suất phát trên mỗi anten của hệ thống MRC 2x1 chỉ bằng một nửa so với hệ thống MRC. Nếu công suất phát trên mỗi anten của hệ thống 2x1 bằng với hệ thống 1x2 thì BER của hệ thống 2x1 sẽ trùng với hệ thống MRC. Do đó, nếu ta kết hợp sơ đồ Alamouti và MRC thì ta sẽ có được hệ thống thu phát thích hợp cho mô hình 2 anten ở trạm gốc BS với một thiết bị di động MS. Tuyến truyền từ BS đến MS sẽ sử dụng mô hình Alamouti với công suất phát thích hợp cho mỗi anten, tuyến truyền từ MS lên BS sẽ sử dụng MRC.

5.3.2. Mô hình MIMO 4x4

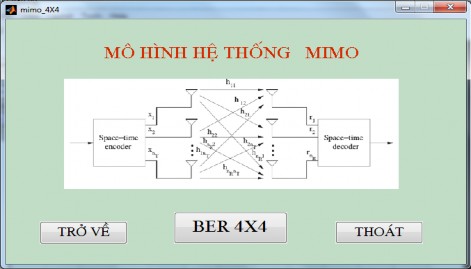
Hình 5.6. Giao diện tính BER của hệ thống MIMO 4x4

Chọn BER 4x4 để thực thi chương trình tính BER của hệ thống 4x4

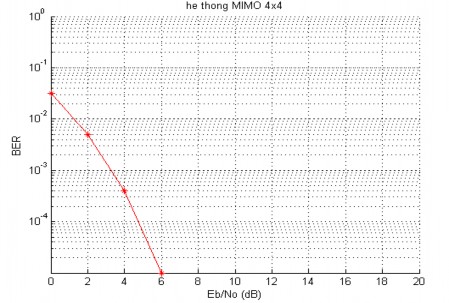
Hình 5.7. BER của hệ thống MIMO 4x4

Hình 5.7. mô tả BER của hệ thống MIMO 4x4 dùng mã hóa không gian-thời gian khối. Với các thông số:

- Chiều dài một khung là 100.

- Số lượng gói là 1000.

- Số lượng anten thu phát là 4.

- Eb/No từ 0 đến 20.

- Mô hình kênh truyền fading và nhiễu Gauss.

- Điều chế dạng QPSK.

Nhận xét:

Quan sát hình 5.7 ta thấy BER của hệ thống MIMO 4x4 tốt hơn so với các hệ thống trên hình 5.5. Như vậy, khi tăng số lượng các anten thu và phát sẽ làm giảm tỷ lệ lỗi bit của hệ thống. Nhưng khi tăng số lượng anten thu và phát sẽ làm tăng giá thành. Do đó tùy theo yêu cầu mà ta sử dụng hệ thống cho thích hợp.

5.4. Dung lượng của hệ thống MIMO

5.4.1. Dung lượng của hệ thống khi không có CSI

Hình 5.8 mô tả dung lượng của hệ thống khi thông tin kênh truyền chỉ được biết tại bên thu với các thông số:

- Số anten phát và thu: có các trường hợp SISO (1x1), SIMO (1x2) MISO (2x1) và MIMO (2x2, 4x4, 8x8).

- Tỷ số tín hiệu trên nhiễu SNR: SNR= 0 đến 20.

- Dung lượng của từng hệ thống được lặp lại 104 lần, sau đó tính dung lượng trung bình để vẽ.

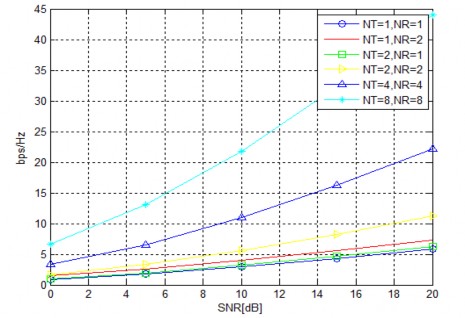
Hình 5.8. Dung lượng của hệ thống khi không có CSI

Nhận xét:

Hình 5.8 cho thấy dung lượng của hệ thống tốt dần lên khi ta tăng số anten phát và anten thu. Xét tại SNR = 10 dB, ta có dung lượng của hệ thống SISO (1x1) là 2.9161, MISO (2x1) là 3.1516, SIMO (1x2) là4.0520, MIMO (2x2) là 5.5495, MIMO (4x4) là 10.9269 ,MIMO (8x28) là 21.8066.