Trường Hợp Csi Được Biết Tại Cả Phía Phát Và Phía Thu

không phụ thuộc vào tín hiệu phát, nghĩa là độ lợi kênh bằng 0. Mặt khác các thành

phần thu, 𝑟′, 𝑖 = 1,2, … , 𝑟 chỉ phụ thộc vào các thành phần phát 𝑥′. Do vậy kênh

𝑖 𝑖

MIMO tương đương từ (1.15) có thể được xem là bao gồm 𝑟 kênh con song song độc lập. Mỗi kênh con được gán với một giá trị riêng của ma trận H, giá trị này tương ứng với độ lợi khuếch đại kênh. Độ lợi công suất kênh bằng với giá trị riêng của ma trận

𝐻𝐻𝐻. Ví dụ, nếu 𝑛𝑇 > 𝑛𝑅, hạng của 𝐻 không thể lớn hơn 𝑛𝑅, phương trình (1.17) cho

ta thấy có không quá 𝑛𝑅 các kênh con có độ lợi khác 0 trong kênh MIMO tương đương.

Hoặc ngược lại nếu 𝑛𝑅 > 𝑛𝑇, thì có lớn nhất 𝑛𝑇 kênh con có độ lợi khác 0 trong kênh MIMO tương ứng.Ma trận hiệp phương và vết của nó với các tín hiệu 𝑟′, 𝑥′và 𝑛′ có thể nhận được từ 1.15.

𝑅𝑟′𝑟′ = 𝑈𝐻 𝑅𝑟𝑟𝑈

𝑅𝑥′𝑥′ = 𝑉𝐻𝑅𝑥𝑥𝑉 (1.18)

Có thể bạn quan tâm!

• Tìm hiểu mô phỏng hệ thống MIMO - OFDM và đánh giá chất lượng hệ thống - 1
• Tìm hiểu mô phỏng hệ thống MIMO - OFDM và đánh giá chất lượng hệ thống - 2
• Kỹ Thuật Ghép Kênh Phân Chia Theo Tần Số Trực Giao.
• Tỷ Số Công Suất Đỉnh Trên Công Suất Trung Bình (Papr)
• Mô Hình Alamouti Với Nhiều Anten Thu

Xem toàn bộ 97 trang tài liệu này.

𝑅𝑛′𝑛′ = 𝑈𝐻𝑅𝑛𝑛𝑈

𝑡𝑟( 𝑅𝑟′𝑟′ ) = 𝑡𝑟(𝑅𝑟𝑟)

𝑡𝑟(𝑅𝑥′𝑥′ ) = 𝑡𝑟(𝑅𝑥𝑥 ) (1.19)

𝑥1

𝑥2

√𝜆1

𝑟1

√𝜆2

𝑟2

𝑥𝑛𝑅

𝜆𝑛𝑅

𝑥𝑛

𝑟𝑛𝑅

𝑅+1

o

𝑥𝑛𝑇

o

𝑡𝑟(𝑅𝑛′𝑛′ ) = 𝑡𝑟(𝑅𝑛𝑛)

Hình 1.3. Sơ đồ khối của kênh MIMO với nT > nR

𝑥1

𝑥2

√𝜆

√𝜆2

𝑟

1

𝑟2

𝑥𝑛

𝜆𝑛𝑇

𝑇

𝑟𝑛𝑇

o

𝑥𝑛 +1

𝑇

o

𝑥𝑛𝑅

Hình 1.4. Sơ đồ khối của kênh MIMO với nR > nT

Các mối quan hệ trên chỉ ra rằng các ma trận hiệp phương sai 𝑟’, 𝑥’, 𝑛’ có cùng tổng các thành phần đường chéo và do đó sẽ có cùng công suất như các tín hiệu ban đầu 𝑟, 𝑥, 𝑛 tương ứng.

Chú ý rằng trong mô hình kênh MIMO tương đương (1.17) các kênh con là độc lập. Do vậy dung lượng của chúng được cộng lại. Giả sử công suất phát từ mỗi anten trong mô hình kênh MIMO tương đương là 𝑃⁄𝑛𝑇, chúng ta có thể đánh giá dung lượng tổng của kênh bằng công thức Shannon, đơn vị tính dung lượng là bit/s. Ta có công thức:

𝐶 = 𝑊 ∑ log2

𝑃

𝑟𝑖

(1 + ) (1.20)

𝜎2

Trong đó W là độ rộng băng của mỗi kênh con, 𝑃𝑟𝑖 là công suất tín hiệu thu trong kênh 𝑖, 𝑃𝑟𝑖 được cho bởi công thức:

𝑃𝑟𝑖

=𝜆𝑖𝑃

𝑛𝑇

(1.21)

Trong đó i

là giá trị riêng của ma trận kênh H, vì vậy dung lượng kênh sẽ là:

𝑖=1

𝐶 = 𝑊 ∑𝑟

log2

(1 +𝜆𝑖𝑃

𝑛𝑇𝜎2

) = 𝑊 log2

𝑟

∏

𝑖=1

(1 +𝜆𝑖𝑃 )

𝑛𝑇𝜎2

(1.22)

Xét mối quan hệ giữa dung lượng kênh và ma trận. Giả sử m =min(nR,nT). Phương trình (1.13) xác định mối quan hệ giữa vecto riêng và giá trị riêng có thể được viết lại như sau:

(𝜆𝐼𝑚 − 𝑄)𝑦 = 0, 𝑦 ≠ 0 (1.22) Trong đó 𝑄 là ma trận Wishart, xác định n hư sau:

𝐻𝐻𝐻 , 𝑛𝑅 < 𝑛𝑇

𝑄 = {

𝐻𝐻𝐻, 𝑛𝑅

≥ 𝑛𝑇

(1.23)

Vậy λ là giá trị riêng của 𝑄, nếu và chỉ ra nếu 𝜆𝐼𝑚 − 𝑄là ma trận riêng. Do đó định thức của 𝜆𝐼𝑚 − 𝑄phải bằng 0:

det(𝜆𝐼𝑚 − 𝑄) = 0 (1.25)

Giá trị riêng λ của ma trận kênh có thể được tìm bằng nghiệm của phương trình (1.25)

Xét đa thức đặc trưng p(λ) từ vế trái của phương trình (1.25):

𝑝(𝜆) = det(𝜆𝐼𝑚 − 𝑄) (1.26) p(λ) có bậc là m nếu mỗi hàng của 𝜆𝐼𝑚 − 𝑄 đóng góp duy nhất một thành phần công suất λ trong khai triển Laplace của định thức det(𝜆𝐼𝑚 − 𝑄). Khi đa thức bậc m

với hệ số phức có đúng m nghiệm, ta có thể biểu diễn đa thức đặc trưng dưới dạng:

𝑝(𝜆) = ∏𝑚

(𝜆 − 𝜆𝑖 )

(1.27)

𝑖=1

Trong đó λi là nghiệm của đa thức đặc trưng p(λ), bằng với giá trị riêng ma trận kênh. Ta có phương trình (1.25) có dạng:

∏𝑚 (𝜆 − 𝜆𝑖 ) = 0 (1.28)

𝑖=1

Ta có phương trình từ 2 vế trái của (1.25) và (1.28):

∏𝑚 (𝜆 − 𝜆𝑖 ) = det(𝜆𝐼𝑚 − 𝑄) (1.29)

2

Thay − 𝑛𝑇𝜎

𝑝

𝑖=1

vào λ trong (1.22) ta có:

∏𝑚

(1 +𝜆𝑖𝑃 ) = det (𝐼

+ 𝑃

𝑄) (1.30)

𝑖=1

𝑛𝑇𝜎2

𝑚 𝑛𝑇𝜎2

Vậy công thức dung lượng từ (1.22) trở thành:

𝐶 = 𝑊 log2

det (𝐼𝑚

+ 𝑃

𝑛𝑇𝜎2

𝑄) (1.31)

Do giá trị riêng khác không của HHH và HHH như nhau, nên dung lượng của kênh tương ứng với các ma trận H và HH cũng như nhau. Chú ý là nếu hệ số kênh biến đổi ngẫu nhiên, công thức (1.22) và (1.31) biểu diễn dung lượng tức thời hoặc thông tin tương hỗ. Dung lượng kênh trung bình có thể thu được bằng cách lấy trung bình tất cả phần thực của hệ số kênh.

1.5.1. Trường hợp CSI được biết tại cả phía phát và phía thu

Khi các tham số của kênh được biết trước ở máy phát, dung lượng có thể tăng lên bằng cách gán công suất phát cho các anten khác nhau theo nguyên tắc “Water- filling”. Đó là đặt công suất phát lớn khi trạng thái của kênh tốt và nhỏ khi trạng thái tồi. Công suất cho kênh 𝑖 được xác định theo công thức:

𝑃𝑖 = (𝜇 −

𝜎2 +

)

𝜆𝑖

(1.32)

Trong đó 𝑎+ được xác định là 𝑎+ = 𝑚𝑎𝑥(𝑎, 0) và μ được xác định sao cho:

∑

𝑟

𝑖=1

𝑃𝑖 = 𝑃 (1.33)

Xét quá trình phân tích giá trị riêng của ma trận H như trong (1.12) Công suất thu ở kênh con i trong mô hình kênh MIMO tương đương là:

𝑃𝑟𝑖 = (𝜆𝑖 𝜇 − 𝜎2)+ (1.34)

Dung lượng kênh MIMO là:

𝐶 = 𝑊 ∑ log2

𝑃

𝑟𝑖

[1 + ] (1.35)

𝜎2

Thay công suất tín hiệu thu từ (1.34) vào (1.35) ta có:

𝐶 = 𝑊 ∑ log

[1 + 1 (𝜆 𝜇 − 𝜎2)+] (1.36)

2 𝜎2 𝑖

Ma trận hiệp phương sai của tín hiệu phát là:

𝐻

𝑅𝑥𝑥 = 𝑉diag(𝑃1, 𝑃2, ⋯ , 𝑃𝑛𝑇 )𝑉 (1.37)

Giả sử có một anten phát và 𝑛𝑅 anten thu. Ma trận kênh được biểu diễn bằng vecto:

𝐻 = (ℎ1, ℎ2, ⋯ , ℎ𝑛𝑅 )

Trong đó toán tử (.)T là chuyển vị ma trận. Khi nR > nT, công thức (1.31) sẽ trở thành:

𝐶 = 𝑊 log

(1 + ∑𝑛𝑅 |ℎ |2 𝑃 ) (1.38)

2 𝑖=1 𝑖 𝜎2

𝑖=1 𝑖

Do 𝐻𝐻𝐻 = ∑𝑛𝑅 |ℎ |2

, áp dụng công thức (1.30) ta có:

𝐶 = 𝑊 log (1 + ∑𝑛𝑅 |ℎ |2 𝑃 ) (1.39)

2 𝑖=1 𝑖 𝜎2

Dung lượng này tương ứng với kết hợp cực đại tuyến tính ở máy thu. Khi các phần tử ma trận kênh bằng nhau và được chuẩn hóa:

|ℎ1

|2 = |ℎ2

|2 = ⋯ |ℎ

𝑛𝑅

2

| = 1

Thì dung lượng theo công thức (1.38) trở thành:

𝐶 = 𝑊 log2

(1 − 𝑛

𝑃 ) (1.40)

𝑅 2

𝜎

Hệ thống này thực hiên tăng ích phân tập gấp 𝑛𝑅 lần kênh 1 anten đơn. Với

𝑛 = 8 và SNR = 20 dB, dung lượng phân tập thu là 9,646 bit/s/Hz.

Với phân tập chọn lọc, thực hiện lựa chọn kênh tốt nhất trong 𝑛𝑅 kênh. Dung lượng của hệ thống này là:

𝐶 = max

{𝑊 log

(1 + 𝑃 |ℎ |2) }

𝑖 2

𝜎2 𝑖

= 𝑊 log

(1 + 𝑃 max {|ℎ |2}) (1.41)

2 𝜎2

𝑖 𝑖

Quá trình chọn lọc cực đại được thực hiện với 𝑖 = 1, 2, … , 𝑛𝑅.

1.5.2. Phân tập phát

Hệ thống có 𝑛𝑇 anten phát và 1 anten thu. Kênh được biểu diễn bằng vector

𝐻 = (ℎ1, ℎ2, ⋯ , ℎ𝑛𝑅 )

Do 𝐻𝐻𝐻 = ∑𝑛𝑇 |ℎ |2

, áp dụng công thức (1.30) ta có:

𝑖=1 𝑖

( ∑𝑛𝑇

2 𝑃

𝐶 = 𝑊 log2 1 +

𝑗=1|ℎ𝑗|

𝑛𝑇

𝜎2) (1.42)

Nếu hệ số kênh bằng nhau và được chuẩn hóa như trong (1.5), dung lượng phân tập phát là:

𝐶 = 𝑊 log2

(1 + 𝑃 ) (1.43)

𝜎2

Dung lượng không tăng theo số lượng anten phát. Công thức này áp dụng với trường hợp máy phát không hiểu kênh truyền. Với kênh truyền được phân bố truyền dẫn, khi máy phát hiểu biết về kênh truyền, ta có thể áp dụng công thức (1.36). Khi hạng của ma trận kênh là 1, chỉ có 1 hạng tử trong tổng theo (1.36) và chỉ ra một giá riêng khác 0 cho bởi công thức:

∑𝑛𝑇 2

𝜆 =

𝑗=1|ℎ𝑗|

(1.44)

Giá trị μ trong điều kiện chuẩn hóa cho bởi công thức:

2

𝜇 = 𝑃 + 𝜎

𝜆

(1.45)

Vì vậy dung lượng là:

( ∑𝑛𝑇

2 𝑃

𝐶 = 𝑊 log2 1 +

𝑗=1|ℎ𝑗|

𝜎2) (1.46)

Nếu hệ số kênh bằng nhau và chuẩn hóa như trong (1.4) ta có:

𝐶 = 𝑊 log2

(1 + 𝑛

𝑃 ) (1.47)

𝑇 2

𝜎

Với nT = 8, SNR = 20 dB, phân tập phát với kênh được biết ở máy phát có dung lượng là 9,646 bit/s/Hz.

1.6. Sơ lượt về kỹ thuật phân tập

Phân tập là kỹ thuật cải thiện độ tin cậy của tín hiệu bằng cách sử dụng hai hay nhiều kênh thông tin liên lạc với các tính chất khác nhau. Phân tập có vai trò quan trọng trong chống fading, nhiễu đồng kênh, lỗi chùm. Kỹ thuật phân tập có thể sử dụng tốt trong truyền đa đường, cho kết quả độ lợi phân tập. Độ lợi phân tập là sự tăng của tỉ số tín hiệu trên nhiễu khi có phân tập hoặc có thể tính là sự rút gọn của công suất phát khi có phân tập.

1.6.1. Phân tập thời gian

Phân tập thời gian có thể thực hiện được bằng cách phát các tin giống nhau trong các khe thời gian khác nhau, điều này tạo ra các tín hiệu bị fading không tương quan ở máy thu.

Phân tập này giúp độ lợi phân tập tăng lên. Tác động của kênh truyền lên tín hiệu được cải thiện. Tuy nhiên, phân tập thời gian làm giảm tốc độ dữ liệu.

1.6.2. Phân tập tần số

Đây là kỹ thuật sử dụng nhiều tần số khác nhau để cùng phát một tin. Các tần số cần dùng phải có khoảng cách đủ lớn để giữ sự độc lập ảnh hưởng của fading với các tần số còn lại. Khoảng tần số ở mức vài lần băng thông kết hợp kênh sẽ đảm bảo đặc tính thống kê fading của các tần số khác nhau sẽ độc lập nhau. Trong thông tin di động, các bản sao của tín hiệu phát được đưa tới máy thu ở dạng dư thừa trong miền tần số để tạo ra trải phổ giống như trải phổ chuỗi trực tiếp, điều chế đa sóng mang, nhảy tần. Kỹ thuật trải phổ có tác dụng khi băng thông kết hợp của kênh nhỏ. Tuy nhiên khi băng thông kết hợp của kênh lớn hơn băng thông trải phổ, thì trải trễ đa đường sẽ nhỏ hơn chu kỳ symbol. Trong trường hợp này, trải phổ sẽ không hiệu quả để tạo ra phân tập tần số. Tương tự như phân tập thời gian, phân tập tần số gây ra tổn thất hiệu quả băng tần do sự dư thừa trong miền tần số.

1.6.3. Phân tập không gian

Phân tập không gian là kỹ thuật sử dụng nhiều anten hay các mảng anten được sắp xếp với các khoảng cách phù hợp để tín hiệu trên các anten độc lập. Khoảng cách yêu cầu thay đổi tùy theo độ cao anten, môi trường truyền và tần số. Khoảng cách điển hình khoảng vài bước sóng.

Phân tập không gian không gây tổn thất trong sử dụng hiệu quả băng tần như phân tập thời gian.

Phân tập không gian còn được gọi là phân tập anten. Phân tập không gian gồm có:

+ Phân tập phân cực: Trong phân tập phân cực, tín hiệu phân cực đứng và phân cực ngang được phát bằng hai anten phân cực khác nhau và cũng thu bằng 2 anten phân cực khác nhau. Điều đó đảm bảo tạo ra 2 tín hiệu không tương quan mà vẫn không cần đặt hai anten cách xa nhau.

+ Phân tập anten phát: Trong phân tập phát, nhiều anten đựơc triển khai ở vị trí máy phát. Tin được xử lí ở máy phát và sau đó được truyền chéo qua các anten.

+ Phân tập anten thu: Trong phân tập thu, nhiều anten được sử dụng ở máy thu để thu các bản sao độc lập của tín hiệu phát. Các bản sao của tín hiệu phát được kết hợp để tăng SNR và giảm fading nhiều đường.

2.1. Khái niệm‌

CHƯƠNG II: KỸ THUẬT OFDM

Kỹ thuật OFDM là kỹ thuật ghép kênh phân chia theo tần số trực giao (Orthogonal Frequency Division Multiplexing). Đó là sự kết hợp giữa mã hóa và ghép kênh. Thường thường nói tới ghép kênh người ta thường nói tới những tín hiệu độc lập từ những nguồn độc lập được tổ hợp lại. Trong OFDM, những tín hiệu độc lập này là các sóng mang con. Đầu tiên tín hiệu sẽ chia thành các nguồn độc lập, mã hóa và sau đó ghép kênh lại để tạo nên sóng mang OFDM.

OFDM là trường hợp đặc biệt của FDM (Frequency Division Multiplex), đây là phương thức phát đa sóng mang theo nguyên lý chia dòng dữ liệu tốc độ cao thành tốc độ thấp hơn và phát đồng thời trên một số sóng mang được phân bố một cách trực giao. Nhờ thực hiện biến đổi chuỗi dữ lệu từ nối tiếp sang song song nên thời gian symbol tăng lên. Do đó, sự phân tán theo thời gian gây bởi trải trễ do truyền dẫn đa đường giảm xuống.

2.1.1. Điều chế đơn sóng mang

Hệ thống đơn sóng mang là một hệ thống có dữ liệu được điều chế và truyền đi chỉ trên một sóng mang.

g(t)

𝒆𝒋𝝎𝒐𝟏

𝒆−𝒋𝝎𝒐𝟏

g*(-t)

Kênh

Hình 2.1. Sơ đồ chung của hệ thống đơn sóng mang

Hình 2.1 mô tả cấu trúc chung của một hệ thống truyền dẫn đơn sóng mang.

Với quá trình điều chế đơn sóng mang, tín hiệu được biểu diễn như sau:

S (t) algt lTs

l

Trong đó al là dữ liệu đầu vào của kí tự thứ l.

2.1.2. Điều chế đa sóng mang

(2.1)

Hệ thống đa sóng mang là hệ thống có dữ liệu được điều chế và truyền đi trên nhiều sóng mang khác nhau. Cụ thể hơn, hệ thống đa sóng mang chia tín hiệu ban đầu thành các luồng tín hiệu khác nhau, và điều chế mỗi dòng tín hiệu với các sóng mang khác nhau. Các tín hiệu được truyền trên các kênh tần số khác nhau, sau đó ghép những kênh này lại theo kiểu FDM. Ở phía thu, bộ tách kênh sẽ đưa đến bộ thu các kênh có tần số khác nhau, sau đó chúng được giải điều chế tạo ra tín hiệu gốc ban đầu.

𝒆𝒋𝝎𝒐𝟏

𝒆−𝒋𝝎𝒐𝟏

𝒆𝒋𝝎𝒌𝟏

𝒆𝒋−𝝎𝒌𝟏

Kên

𝒆𝒋𝝎𝑵𝟏

𝒆−𝒋𝝎𝑵𝟏

g(t)

+

g*(-t)

g(t)

g*(-t)

g(t)

g*(-t)

Hình 2.2. Cấu trúc truyền dẫn hệ thống đa sóng mang

Hệ thống đa sóng mang, tín hiệu có thể được biểu diễn như sau:

𝑆(𝑡) = 1

∑ ∑𝑁−1 𝑎

𝑒𝑗2𝜋𝑘(𝑡−𝑙𝑇𝑠(𝑁+𝐿)

(2.2)

Trong đó:

√𝑁 𝑙

𝑘=0

𝑙,𝑘

𝑎𝑙,𝑘: là dữ liệu đầu vào được điều chế trên sóng mang nhánh thứ 𝑘 trong symbol OFDM thứ 𝑙

N: số sóng mang nhánh

L: Chiều dài tiền tố lặp (CP)

Khoảng cách giữa các sóng mang nhánh là:

2.1.3. Tín hiệu trực giao

1 = 1

𝑇 𝑁𝑇𝑆

Các tín hiệu là trực giao nếu chúng độc lập với nhau. Tín hiệu trực giao có tính chất cho phép truyền và thu tốt nhiều tín hiệu trên cùng một kênh truyền mà không gây ra nhiễu xuyên kí tự giữa các tín hiệu này.

Tính trực giao của tín hiệu được thể hiện ở dạng phổ của nó trong miền tần số. Trong miền tần số, mỗi sóng mang con của tín hiệu trực giao có đáp ứng tần số là sin hay sin(x)/x. Biên độ hàm sine có dạng búp chính hẹp và nhiều búp phụ có biên độ giảm dần khi càng xa tần số trung tâm. Mỗi sóng mang của tín hiệu có biên độ đỉnh tai tần số trung tâm của nó và bằng 0 tại tần số trung tâm của sóng mang khác. Do đó ta gọi các tín hiệu trực giao nhau.

Ví dụ: giả sử 4 tín hiệu trực giao được điều chế bởi 4 sóng mang con hình sin

sau:

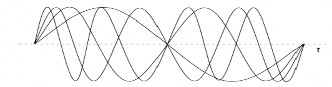
Hình 2.3. Bốn sóng mang trực giao nhau

Xem tất cả 97 trang.