CHƯƠNG 3. PHÂN LỚP DỮ LIỆU MẤT CÂN ĐỐI BẰNG CÂY QUYẾT ĐỊNH
Một phương pháp được đề xuất để cải tiến thay đổi và phát triển dựa trên thuật toán C4.5 bằng cách sử dụng giá trị AUC [22] thay cho Gain-entropy [21], được đặt tên AUC4.5 để phân lớp dữ liệu mất cân đối cho cả hai mục đích đó là: Mục tiêu học và độ đo đánh giá.
3.1 Đường cong Receiver Operating Characteristic (ROC)
ĐỒ THỊ ĐƯỜNG CONG ROC
1.0
0.8 B
0.6
0.4
0.2
0.0
0.0 0.2 0.4 0.6
0.8
1.0
False Positive Rate
True Positive Rate
ROC [22] là một đồ thị được sử dụng khá phổ biến trong kiểm chứng các mô hình phân loại nhị phân. Đường cong này được tạo ra bằng cách biểu diễn tỷ lệ dự báo True Positive Rate (TPR) dựa trên tỷ lệ dự báo False Positive Rate (FPR). Trong machine learning chúng ta gọi TPR là xác xuất dự báo đúng một sự kiện là Positive. FPR (là Probability of false alarm - tỷ lệ cảnh báo sai), một sự kiện là Negative nhưng coi nó là Positive và tỷ lệ này tương ứng với xác suất mắc sai lầm. Như vậy đường cong ROC sẽ thể hiện mối quan hệ, sự đánh đổi và ý nghĩa lựa chọn một mô hình phù hợp của độ nhạy và tỷ lệ cảnh báo sai. Hình 3-1: biểu diễn tỷ lệ dự báo TPR dựa trên tỷ lệ dự báo FPR.
Hình 3-1: Đồ thị ROC biểu diển một bộ phân lớp rời rạc của xác suất B
3.2 Diện tích dưới đường cong ROC
Dựa trên đường cong ROC, ta có thể chỉ ra rằng một mô hình có hiệu quả hay không. Một mô hình hiệu quả khi có FPR thấp và TPR cao, tức tồn tại một điểm trên đường cong ROC gần với điểm có toạ độ (0, 1) trên đồ thị (góc trên bên trái). Đường cong càng gần thì mô hình càng hiệu quả. Có một thông số nữa dùng để đánh giá được gọi là Area Under the Curve (AUC). Đại lượng này chính là diện tích nằm dưới đường cong ROC – phần hình được tô đường nét ô vuông. Giá trị này là một số dương nhỏ hơn hoặc bằng 1. Giá trị này càng lớn thì mô hình càng tốt.
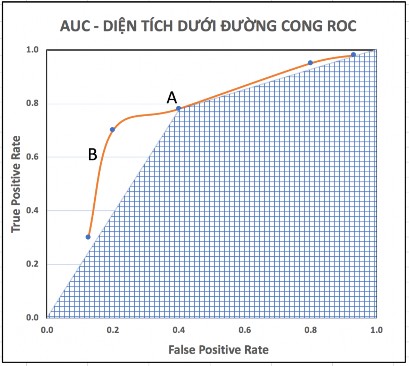
Hình 3-2: AUC – diện tích dưới đường cong ROC của một bộ phân lớp A và một bộ phân lớp xác suất B
3.3 Độ đo đánh giá hiệu suất phân lớp
Để đánh giá một thuật toán phân lớp có hiệu quả hay không đều cần có những độ đo đánh giá. Trong phân lớp nhị phân, hiệu suất dự đoán của một bộ phân lớp thường được sử dụng ma trận nhầm lẫn (confusion matrix) [22] ở Bảng I.
Bảng 3-1: Ma trận nhầm lẫn
thể hiện hiệu suất dự đoán trong bộ phân lớp nhị phân
Predicted class (Lớp dự đoán) | |||
Positive | Negative | ||
Actual class (Lớp thực tế) | Positive | TP | FN |
Negative | FP | TN |
Có thể bạn quan tâm!
-
Thuật Toán Phân Lớp Dữ Liệu Mất Cân Đối Bằng Cây Quyết Định -
Các Vấn Đề Trong Khai Thác Dữ Liệu Sử Dụng Cây Quyết Định -
Đánh Giá Độ Chính Xác Của Mô Hình Phân Lớp -
Cây Quyết Định Với Thuật Toán C4.5 Bằng Cách Giảm Nhiều Impurity -
Sử dụng cây quyết định phân lớp dữ liệu mất cân đối - 8 -
Sử dụng cây quyết định phân lớp dữ liệu mất cân đối - 9
Xem toàn bộ 81 trang tài liệu này.
Nguồn từ: T. Fawcett, “An introduction to ROC analysis” [22].
Bảng I mô tả sự phân bố nhầm lẫn giữa hai lớp: Positive là nhãn lớp của các phần tử lớp thiểu số. Negative là nhãn lớp của các phần tử lớp đa số.
True Positive (TP): Mẫu mang nhãn positive, phân lớp ĐÚNG vào lớp positive. False Negative (FN): Mẫu mang nhãn positive, phân SAI vào lớp negative.
False Positive (FP): Mẫu mang nhãn negative, phân lớp SAI vào lớp positive. True Negative (FN): Mẫu mang nhãn negative, phân lớp ĐÚNG vào lớp negative.
Dựa vào bảng I, chúng ta xác định được một số độ đo đánh giá sau [22].
+ 𝑇𝑃𝑅 = 𝑇𝑃
𝑇𝑃+ 𝐹𝑁
TPR: Xác suất dự báo một sự kiện là Positive (lớp thiểu số)
- 0 TPR 1
- Nếu FN = 0 => TPR = 1 là tốt nhất.
+ 𝐹𝑃𝑅 = 𝐹𝑃
𝐹𝑃+ 𝑇𝑁
(3.18)
(3.19)
FPR: Tỉ lệ cảnh báo sai (False Alarm Rate),
một sự kiện là 𝑁𝑒𝑔𝑎𝑡𝑖𝑣𝑒 nhưng xem nó là 𝑃𝑜𝑠𝑖𝑡𝑖𝑣𝑒
- 0 FPR 1
- Nếu FP = 0 => FPR = 0 là tốt nhất.
+ 𝐴𝑈𝐶 = 1+ 𝑇𝑃𝑅− 𝐹𝑃𝑅
2
(3.20)
- 0 AUC 1
- Giá trị AUC càng lớn thì mô hình càng tốt.
3.4 Thuật toán AUC4.5
Một số cải tiến từ chính thuật toán C4.5 [21] như sau:
Thích hợp cho tập dữ liệu mất cân đối.
Không dùng phương pháp Resampling hoặc Cost-sensitive: để tránh tình trạng mất mát dữ liệu, quá khớp, bùng nổ kích thước cây quyết định…
Dùng ma trận nhầm lẫn và các giá trị TPR, FPR, AUC [22],… để làm độ đo đánh gía cũng như huấn luyện tập dữ liệu.
Tiêu chí tách và phương pháp cắt tỉa: Dùng giá trị AUC [22] thay cho Gain-entropy.
Mục tiêu học của các bộ phân lớp và độ đo đánh giá: Dùng giá trị AUC thay cho độ chính xác tổng thể.
3.4.1 Ý tưởng chính thuật toán AUC4.5
Thuật toán xét tất cả các phép thử có thể để phân chia tập dữ liệu đã cho và chọn ra một phép thử có giá trị AUCGainRatio tốt nhất. AUCGainRatio là một đại lượng để đánh giá độ hiệu quả của thuộc tính, dùng để thực hiện phép tách và cắt tỉa trong thuật toán để phát triển cây quyết định. AUCGainRatio được tính dựa trên công thức sau.
Tính AUC lớn nhất của nhãn lớp (class labels) của nút thứ i:
𝑇
𝑚𝐴𝑈𝐶(𝑐𝑙𝑖) = 𝑀𝑎𝑥𝐴𝑈𝐶({ 𝑖})
Độ lợi AUC (AUC gain):
𝐴𝑈𝐶𝐺𝑎𝑖𝑛(𝐴𝑡𝑡𝑟𝑖𝑗) = 𝑚𝐴𝑈𝐶 − 𝐵𝑎𝑠𝑒𝑙𝑖𝑛𝑒
Với
𝐴𝑈𝐶𝐺𝑎𝑖𝑛𝑅𝑎𝑡𝑖𝑜(𝐴𝑡𝑡𝑟𝑖𝑗) =
𝐴𝑈𝐶𝐺𝑎𝑖𝑛(𝐴𝑡𝑡𝑟𝑖𝑗)
𝑆𝑝𝑙𝑖𝑡𝐼𝑛𝑓𝑜(𝐴𝑡𝑡𝑟𝑖𝑗)
|𝑇𝑖|
|𝑇𝑖|
𝑆𝑝𝑙𝑖𝑡𝐼𝑛𝑓𝑜(𝐴𝑡𝑡𝑟𝑖𝑗) = − ∑
𝑖∈ 𝑉𝑎𝑙𝑢𝑒(𝐴𝑡𝑡𝑟𝑖𝑗)
|𝑇| 𝑙𝑜𝑔2 |𝑇|
Trong đó:
- 𝐵𝑎𝑠𝑒𝑙𝑖𝑛𝑒 = 0.5; Đ𝑖ề𝑢 𝑛à𝑦 𝑥ả𝑦 𝑟𝑎 𝑡𝑟𝑜𝑛𝑔 𝑡𝑟ườ𝑛𝑔 ℎợ𝑝 𝑚ộ𝑡 𝑛ú𝑡 𝑐ℎ𝑎.
- Value (𝐴𝑡𝑡𝑟𝑖𝑗): là tập các giá trị của thuộc tính 𝐴𝑡𝑡𝑟𝑖𝑗
𝑇
- 𝑖: là tập con của tập T ứng với thuộc tính 𝐴𝑡𝑡𝑟𝑖𝑗 = giá trị là 𝑣𝑖
Chọn thuộc tính phân nhánh mà giá trị AUC lớn nhất của cây. Giá trị AUC lớn nhất thì độ chính xác phân lớp càng cao.
3.4.2 Một số giải thuật chính
3.4.2.1 Giải thuật chính AUC4.5
Algorithm 1. AUC4.5
Input: Tập huấn luyện D = {Dgrow, Dvalid}
Output: Trả về cây quyết định cuối cùng final_tree
(1) full_tree GrowTree (Dgrow)
(2) if full_tree is a single leaf (root) node then
(3) final_tree ← full_tree
(4) else
(5) candidate_tree ← PruneTree(full_tree)
(6) final_tree ← ValidTrees(candidate_tree, Dvalid)
(7) end if
(8) return final_tree
AUC4.5 là giải thuật chính, gọi các đến các giải thuật GrowTree, PruneTree và ValidTrees. Giải thuật này trả về cây quyết định cuối cùng mà được học từ tập huấn luyện D. Tập huấn luyện D
được chia làm hai tập con. Một dùng để huấn luyện một cây quyết định (Dgrow), tập còn lại được dùng ở bước tỉa cây (Dvalid) để tránh trường hợp quá khớp cây quyết định.
3.4.2.2 Giải thuật phát triển cây GrowTree
GrowTree là giải thuật đệ quy được sử dụng để thêm các nhánh (branches) và các nút con (child nodes). Giải thuật GrowTree gọi đến giải thuật AUCsplit – được định nghĩa trong Algorithm 3 và gọi đến chính nó.
Algorithm 2. GrowTree
Input: TD tập dữ liệu huấn luyện đầu vào của một nút
Output: Trả về cây quyết định decision tree
(1) if TD has a single class then
(2) return one node of TD
(3) else
// Find the best splitting attribute 𝐴𝑡𝑡𝑟𝑖, the splits (values of attributes) {𝑣𝑖}
// the sub-datasets {DT𝑖} , and their class labels {𝑐l𝑖}
(4) (𝐴𝑡𝑡𝑟𝑖, {𝑣𝑖}, {𝑇𝐷𝑖}, {𝑐𝑙𝑖}) ← 𝐴𝑈𝐶𝑆𝑝𝑙𝑖𝑡(𝑇𝐷)
(5) for each i do
(6) Add a branch for 𝑣𝑖
(7) Add a child node with 𝑇𝐷𝑖
(8) Assign the class label cli to 𝑇𝐷𝑖
(9) Add a subtree GrowTree(𝑇𝐷𝑖) to this branch
(10) end for
(11) Return the decision tree
(12) end if
Giải thuật đề xuất AUC4.5 khác với giải thuật C4.5 gốc, khi các nút con thu được bằng cách tách các nút cha của chúng. Việc tính một giá trị nhiễu (impurity) như độ hỗn loạn thông tin thì không yêu cầu các nhãn lớp khi trả về một nút con. Trong khi đó, giải thuật đề xuất xem xét sự
khác nhau về giá trị AUC giữa một nút cha và các nút con của nó, do đó phương pháp đề xuất dùng AUCGain thay thế InfomarionGain. Do đó các nút con phải gắn nhãn lớp để tính các giá trị AUC tương ứng.
3.4.2.3 Giải thuật tách (splitting criteria) AUCsplit
Algorithm 3. AUCsplit
Input: ND dữ liệu đầu vào
Output: Trả về thuộc tính tương ứng với AUCGainRatio lớn nhất
(1) Baseline MaxAUC (ND) // this value is 0.5 If the input of MaxAUC is
a single node.
(2) for each attribute j do
(3) Divide ND into {T𝑖} by j = 𝑣𝑖 (ND)
(4) (mAUC, {𝑐l𝑖}) MaxAUC (ND)
𝐴𝑡𝑡𝑟𝑖
(5) AUCGain mAUC – Baseline
(6) 𝑆𝑝𝑙𝑖𝑡𝐼𝑛𝑓𝑜(
) = − ∑ |𝑇𝑖| 𝑙𝑜𝑔
|𝑇𝑖|
𝑗 𝑖∈ 𝑉𝑎𝑙𝑢𝑒(𝐴𝑡𝑡𝑟𝑖𝑗) |𝑇|
2 |𝑇|
(7) AUCGainRatio 𝐴𝑈𝐶𝐺𝑎𝑖𝑛
𝑆𝑝𝑙𝑖𝑡𝐼𝑛𝑓𝑜
(8) end for
(9) Trả về thuộc tính tương ứng với AUCGainRatio lớn nhất
Giải thuật tính MaxAUC
Algorithm 4. MaxAUC
Input: {𝑆𝐷𝑖} dữ liệu đầu vào
Output: (𝑚𝐴𝑈𝐶, {𝑐𝑙𝑖}) trả về giá trị AUC lớn với nhãn lớp tương ứng
(1) if cardinality of {𝑆𝐷𝑖} is 1 then
Return mAUC ←0.5 and 𝑐𝑙←𝑚𝑎𝑗𝑜𝑟𝑖𝑡𝑦 𝑐𝑙𝑎𝑠𝑠 𝑙𝑎𝑏𝑒𝑙
(2) else
(3) Compute AUC values for all possible combinations of class labels assigned to {𝑆𝐷𝑖}
(4) Find the maximum AUC
(5) Return mAUC and the corresponding class labels {𝑐𝑙𝑖}
(6) end if
Hàm AUCsplit() được dùng để quyết định thuộc tính tốt nhất cho việc tách nhánh dựa trên việc tính toán giá trị AUC lớn nhất khi gọi hàm MaxAUC() với nhãn lớp tương ứng. Hàm MaxAUC() tính giá trị AUC lớn nhất cho một nút cha hoặc một tập các nút con.
Nếu giá trị đầu vào của hàm MaxAUC() là một nút đơn thì giá trị AUC = 0.5, vì chỉ có duy nhất
1 nhãn lớp được gán cho nút này, và kết quả là {TPR = 1, FPR = 1} hoặc TPR = 0, FPR = 0}.
Nếu dữ liệu đầu vào của hàm MaxAUC() là 1 tập các nút (con) thì có các trường hợp gán nhãn lớp khác nhau. Nếu số phần tử của {SDi} là n, thì có (2n - 2) lần gán.
Ví dụ: Giả sử có 3 nút con được tạo nhánh ra từ một nút cha.
+ Thì có 6 khả năng gán nhãn lớp được đưa ra cho các nút:
{+, , } { , +, } { , , +} {+, +, } {+, , +} và {, +, +}.
+ Lấy giá trị lớn nhất AUC trong 6 trường hợp trên để gán nhãn lớp.
Nếu trường hợp thuộc tính có giá trị liên lục thì tập dữ liệu {ND} được chia làm hai phần {𝑆𝐷1,
𝑆𝐷2} bởi một giá trị ngưỡng (threshold value). Vì thế, trong hàm AUCsplit(), dòng 3-7 được lặp lại cho tất cả các giá trị ngưỡng có thể nếu thuộc tính thứ j là thuộc tính liên tục.