Giải Thuật Kiểu Viterbi Để Tìm Phân Tích Tốt Nhất

Luận án chưa thử nghiệm trên câu phức là dạng câu có từ hai cụm chủ vị trở lên nhưng có một cụm bao các cụm còn lại, ví dụ “cái áo hôm qua cậu mua rất đẹp” có hai cụm chủ vị “cậu mua” “cái áo đẹp” , cụm “cái áo đẹp” bao cụm còn lại. Thật ra, một số trường hợp đã có thể phân tích với bộ phân tích câu ghép của chúng tôi, như câu “Nó bảo rằng nó không đi nữa”.Tuy nhiên một số trường hợp cần dùng phương pháp học máy để nhận ra giới hạn mệnh đề.

3.2.5. Độ phức tạp tính toán

Theo Sleator [111], chi phí thời gian của giải thuật phân tích liên kết (khi chưa lược tỉa) là với một văn phạm xác định là O(n3 ) với n là độ dài câu (số từ trong câu), chi phí này cũng tương đương với chi phí thời gian của các giải thuật phân tích sử dụng văn phạm phi ngữ cảnh. Khi phân tích cú pháp ngôn ngữ tự nhiên, n không lớn nên phần lớn chi phí thời gian là do việc tìm kiếm các luật phù hợp trong văn phạm. Nếu xét cả kích thước văn phạm thì giải thuật phân tích liên kết có chi phí O(n3m), m là số dạng tuyển trung bình của các từ trong câu. Trong khi đó, độ phức tạp của các giải thuật CYK và Earley cho văn phạm phi ngữ cảnh theo Jurafsky [70] là O(n3 |G|), |G| là số sản xuất của văn phạm phi ngữ cảnh.

Chi phí thời gian chủ yếu chính là do giai đoạn lược tỉa. Trong tiếng Việt, do từ không biến đổi hình thái nên mỗi từ phải có nhiều mối liên hệ với các từ chỉ thì, thể, số…, Số lượng dạng tuyển trung bình (chưa lược tỉa) của mỗi từ khoảng 10.000. Từ [111] có thể thấy giải thuật lược tỉa có chi phí O(nm).

Nếu quá trình phân đoạn diễn ngôn chia câu thành k mệnh đề, độ dài trung bình mỗi mệnh đề còn n/k, chi phí thời gian trung bình sẽ giảm k2 lần. Chi phí phân đoạn diễn ngôn là O(n), chi phí duyệt cây diễn ngôn là cây nhị phân gồm k/2 nút lá (không duyệt nút lá) ứng với k mệnh đề không quá O(k).Như vậy k càng lớn, chi phí thời gian sẽ càng nhỏ. Tuy nhiên nếu k bằng 1 thì chi phí sẽ lớn hơn chi phí phân tích câu đơn.

Thực nghiệm với tập câu mẫu thứ nhất ở bảng 3.5, cho thấy thời gian để phân tích tập mẫu theo kiểu liên kết liên từ là 296.153 mili giây, trong khi thời gian phân tích câu đó bằng cách phân tích riêng từng mệnh đề là 217.324 mili giây, giảm đáng kể so với phân tích kiểu liên kết liên từ.

3.3.Khử nhập nhằng

Như đã trình bày ở chương 2, Jurafsky [70] nêu ra hai vấn đề chủ yếu trong nhập nhằng cú pháp: nhập nhằng thành phần và nhập nhằng liên hợp. Nhập nhằng thành phần (attachment ambiguation) xảy ra khi một cấu trúc có thể tham gia các bộ phận khác nhau trên cây phân tích, tạo ra những phân tích khác nhau. Nhập nhằng liên hợp (cordination ambiguation) xảy ra khi gặp những cụm từ liên kết với nhau bằng liên từ liên hợp “và”, “hoặc”, “hay”…Nhập nhằng địa phương (local ambiguation) cũng được tính đến khi một từ có thể nhận các nhãn từ loại khác nhau. Vấn đề nhập nhằng địa phương của mô hình liên kết một phần đã được giải quyết trong quá trình phân tích cú pháp. Khác với các mô hình khác, từ không được gán nhãn trước khi phân tích cú pháp mà được gán nhãn dựa trên liên kết mà nó tham gia. Một từ có nhiều nghĩa sẽ xuất hiện trong những công thức khác nhau, tuy nhiên chỉ những tổ hợp các từ và nhãn thỏa các yêu cầu liên kết mới được chấp nhận. Do vậy số lượng phân tích liên kết của mỗi câu nhỏ hơn đáng kể so với số lượng cây cú pháp của mô hình phi ngữ cảnh.

Trong phần này nói đến việc giải quyêt vấn đề nhập nhằng thành phần và nhập nhằng liên hợp. Đối với nhập nhằng thành phần, luận án đã chọn cách tiếp cận của Lafferty và đồng nghiệp [79] với mô tả chung về một mô hình xác suất trigram. Từ mô tả này, luận án phải xây dựng giải thuật khử nhập nhằng cho ứng dụng của mình.

Có thể bạn quan tâm!

Xem toàn bộ 305 trang tài liệu này.

3.3.1. Khử nhập nhằng thành phần

Vấn đề nhập nhằng thành phần xảy ra khi một câu có nhiều hơn một phân tích liên kết. Câu đươc xét ở đây là câu đơn. Nếu là câu ghép, sau khi phân tách thành mệnh đề, mới giải quyết vấn đề nhập nhằng.

Theo mô hình trigram [79], việc khử nhập nhằng không phải là tính xác suất của mỗi phân tích, tìm ra câu có xác suất lớn nhất, mà là sử dụng mô hình Markov ẩn (HMM) dự đoán câu có xác suất lớn nhất. Hai vấn đề chính cần giải quyết phục vụ mục đích này là:

Tìm câu có xác suất lớn nhất theo giải thuật kiểu Viterbi.
Cập nhật lại xác suất của các sản xuất.

3.3.1.1. Giải thuật kiểu Viterbi để tìm phân tích tốt nhất

Trong [79] đã giới thiệu mô hình xác suất cho văn phạm liên kết tương tự như mô hình đã được mô tả ở mục 1.1.2. cho văn phạm phi ngữ cảnh. Nếu trong văn phạm phi ngữ cảnh, thao tác cơ bản là viết lại thì trong văn phạm liên kết, thao tác cơ bản lại là tìm liên kết. Đối tượng tương đương với sản xuất của văn phạm phi ngữ cảnh trong văn phạm liên kết là liên kết. Mỗi liên kết phụ thuộc vào hai kết nối: kết nối phải và kết nối trái cùng tên nối hai từ L và R . Như vậy tham số của văn phạm liên kết là:

Pr ( W, d, O | L, R, l, r ) (3.1)

O có thể nhận các giá trị →, ←, ↔ thể hiện hướng liên kết. Có thể hiểu là: cho từ L có kết nối phải là l và từ R có kết nối trái r, tham số là xác suất của sự kiện: tồn tại từ W nằm giữa L và R, dạng tuyển d của W liên kết được với L hoặc R hoặc cả hai. Xác suất (3.1) phân rã thành:

Pr ( W, d, O | L, R, l, r ) =

Pr (W | L, R, l, r ) × Pr ( d | W, L, R, l, r ) × Pr ( O | d, t, p, q, l, r ) (3.2)

Vì ta đang xét đến các xác suất điều kiện trên một tập sự kiện quá lớn cho một văn phạm với từ vựng của ngôn ngữ tự nhiên, trên thực tế không thể ước lượng được xác suất này. Do vậy nó cần được xấp xỉ bằng công thức [79]:

Pr ( W, d, O | L, R, l, r ) ≈ Pr (W | L, R, l, r ) × Pr (d | W, l, r ) × Pr (O | d, l, r ) (3.3)

Xác suất của một phân tích liên kết (linkage) là tích của xác suất của mọi liên kết trong nó. Bây giờ cần biểu diễn phân tích liên kết L bởi một tập các liên kết L = {(W, d, O, L, R, l, r)} cùng với dạng tuyển đầu tiên d0. Xác suất của L là:

Pr ( S, L ) = Pr ( W0, d0 ) ∏ Pr ( W, d, O | L, R, l, r )

Ví dụ: Một văn phạm liên kết xác suất có lưu trữ các tham số sau (Từ thứ n là từ “giả” Wn được dùng trong phân tích theo giải thuật trong hình 3.4):

Pr ( tôi, ( ) ( SV ) ) = 0.7
Pr ( mua, (SV)(O), ← | tôi, Wn , SV, NIL) = 0.06
Pr ( hoa, ( O, NcNt3 )( ), ← | mua, Wn , O, NIL) = 0.03
Pr ( bông, (McN)(NcNt3), → | mua, hoa, NIL, NcNt3) = 0.05
Pr ( một, ( )(McN), → | mua, bông, NIL, McN) = 0.06
Pr ( bông, (O, McN)(NcNt3), ↔ | mua, Wn , O, NIL) = 0.00001
Pr ( hoa, (NcNt3)( ) ← | bông, Wn, NcNt3, NIL) = 0.07 (3.4)

Giả sử câu “Tôi mua một bông hoa” có hai phân tích L1 và L2 như trong hình 3.20 dưới đây:

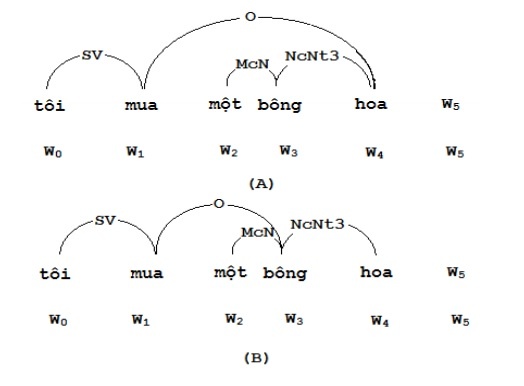
Hình 3.20. Hai phân tích của câu “Tôi mua một bông hoa”

Xác suất cho phân tích L1 (hình 3.20 (A)) là:

Pr (L1) = Pr ( 0, ( )( SV ) ) × Pr ( 1, (SV)(O), ← | 0, 5 , SV, NIL ) ×
Pr ( 4, ( O, NcNt3 )( ), ← | 1, n, O, NIL ) ×
Pr ( 3, (McN)(NcNt3), → | 1, 4, NIL, NcNt3 ) ×
Pr ( 2, ( )(McN), → | 1, 3, NIL, McN )
= 0.7 * 0.06 * 0.03 * 0.05 * 0.06
= 3.78E-5

Trong khi xác suất của phân tích L2 (hình 3.20. (B)) là:

Pr (L2) = Pr ( 0, ( )( SV ) ) × Pr ( 1, (SV)(O), ← | 0, 5 , SV, NIL ) ×
Pr ( bông, (O, McN)(NcNt3), ↔ | mua, Wn , O, NIL ) ×
Pr ( một, ( )(McN), → | mua, bông, NIL, McN ) ×
Pr ( hoa, (NcNt3)( ) ← | bông, Wn, NcNt3, NIL )
= 0.7 × 0.06 × 0.00001 × 0.06 × 0,7
= 2E-8

Nếu phải chọn một trong hai phân tích thì L1 sẽ được chọn.

Trong [79] chỉ đưa ra mô hình xác suất cho văn phạm liên kết với xác suất trong và xác suất ngoài tương tự xác suất tiến và xác suất lùi trong mô hình HMM. Luận án đã đề xuất giải thuật kiểu Viterbi cho mô hình văn phạm liên kết.

Hình 3.21. Giải thuật kiểu Viterbi để dự đoán phân tích có xác suất cao nhất