Trang chủ / Bảo Mật

Ưu Điểm Và Nhược Điểm Của Hệ Mã Hóa Không Đối Xứng

dụng quan trọng của DES là trong giao dịch ngân hàng Mỹ - (ABA) DES đã được dùng để mã hoá các số định danh cá nhân (PIN) và hỗ trợ trong xác thức việc chuyển tài khoản bằng máy ATM. DES cũng được Hệ thống chi trả giữa các nhà băng của Ngân hàng hối đoái (CHIPS) dùng để xác thực các giao dịch lớn. DES còn được sử dụng rộng rãi trong các tổ chức chính phủ. Chẳng hạn như bộ năng lượng, Bộ Tư pháp và Hệ thống dự trữ liên bang Mỹ.

4.3. HỆ MÃ HÓA KHÔNG ĐỐI XỨNG

4.3.1. Khái niệm về hệ mã hóa không đối xứng

Các thuật toán mã hóa khóa đối xứng có một nhược điểm là nếu hai người dùng muốn trao đổi thông tin bí mật cần phải trao đổi khóa bí mật trước đó. Khóa bí mật này cần phải được trao đổi theo một cách thức an toàn, không phải bằng các phương thức thường dùng để liên lạc trong môi trường mở vì dễ bị lộ. Điều này khó thực hiện và nói chung là không thể đảm bảo bí mật, nhất là trong trường hợp muốn trao đổi thông tin với nhiều đối tác thì thực tế là không thực hiện được.

Vì vậy mã hóa khóa công khai (hay khóa bất đối xứng) được đưa ra như là một giải pháp thay thế. Thực ra mã hóa bất đối xứng không thay thế hoàn toàn mã hóa đối xứng mà người ta sử dụng đồng thời cả hai loại để bổ sung, hỗ trợ cho nhau.

Năm 1874, William Stanley Jevons xuất bản một cuốn sách mô tả mối quan hệ giữa các hàm một chiều (one way function) với mật mã học, đồng thời đi sâu vào bài toán phân tích ra thừa số nguyên tố (sử dụng trong thuật toán RSA). Tháng 7 năm 1996, một nhà nghiên cứu đã bình luận về cuốn sách trên như sau: Trong cuốn The Principles of Science: A Treatise on Logic and Scientific Method được xuất bản năm 1890, William S. Jevons đã phát hiện nhiều phép toán rất dễ thực hiện theo một chiều nhưng rất khó theo chiều ngược lại, điều đó chứng tỏ nhiều thuật toán mã hóa thực hiện rất dễ dàng trong khi giải mã thì rất khó khăn. Chẳng hạn tác giả nêu ra bài toán: ta có thể nhân để tìm tích số của các số nguyên tố nhưng

ngược lại, muốn phân tích một số tự nhiên khá lớn ra các thừa số nguyên tố thì là điều không dễ dàng (thuật toán Euclide).

Đây chính là nguyên tắc cơ bản của thuật toán mã hóa khóa công khai RSA (tuy rằng tác giả không phải là người phát minh ra mã hóa khóa công khai). Thuật toán mã hóa khóa công khai được thiết kế lần đầu tiên bởi James H. Ellis, Clifford Cocks và Malcolm Williamson tại Anh vào đầu thập kỷ 70 của thế kỷ trước. Thuật toán đó sau này được phát triển và biết đến dưới tên thuật toán Diffie-Hellman và là một trường hợp đặc biệt của thuật toán RSA, tuy nhiên những thông tin này chỉ được tiết lộ ra vào năm 1997.

Thuật toán mã hóa khóa công khai có cơ sở hoàn chỉnh đầu tiên được Ron Rivest, Adi Shamir và Leonard Adleman (Gọi tắt là RSA) khởi xướng vào năm 1977 tại Học viện Kỹ thuật Massachusett - MIT (Massachusett Institute of Technology). Công trình này được công bố vào năm 1978 và thuật toán được đặt tên là thuật toán RSA - theo 3 chữ cái đầu của các đồng tác giả. RSA sử dụng phép toán lũy thừa theo modulo (với modulo được tính bằng tích số của 2 số nguyên tố lớn) để mã hóa và giải mã cũng như tạo chữ ký số. Độ an toàn của thuật toán được đảm bảo vì không tồn tại kỹ thuật hiệu quả để phân tích một số rất lớn thành thừa số nguyên tố.

Mã hóa khóa công khai là một dạng mã hóa cho phép người sử dụng trao đổi các thông tin mật mà không cần phải trao đổi các khóa bí mật trước đó, điều này được thực hiện bằng cách sử dụng một cặp khóa có quan hệ toán học với nhau là khóa công khai (Public key) và khóa riêng (Private key) hay khóa bí mật (Secret key).

Có thể bạn quan tâm!

Xem toàn bộ 194 trang tài liệu này.

Điều quan trọng đối với hệ thống là không thể (hoặc rất khó) tìm ra khóa bí mật nếu chỉ biết khóa công khai, hệ thống mật mã hóa khóa công khai có thể sử dụng với các mục đích:

- Mã hóa: giữ bí mật thông tin và chỉ có người có khóa bí mật mới giải mã được.

- Tạo chữ ký số: cho phép kiểm tra một văn bản xem nó có phải đã được tạo với một khóa bí mật nào đó hay không.

- Thỏa thuận khóa: cho phép thiết lập khóa để trao đổi thông tin mật giữa hai bên.

Thông thường, các kỹ thuật mã hóa khóa công khai đòi hỏi khối lượng tính toán nhiều hơn các kỹ thuật mã hóa khóa đối xứng nhưng do những ưu điểm nổi bật nên chúng được sử dụng nhiều. Thuật toán mã hóa bất đối xứng sử dụng hai khóa: khóa công khai (hay khóa công cộng) và khóa bí mật (hay khóa riêng). Mỗi khóa là những số cố định sử dụng trong quá trình mã hóa và giải mã, khóa công khai được công bố rộng rãi cho mọi người và được dùng để mã hóa, những thông tin được mã hóa bằng khóa công khai chỉ có thể được giải mã bằng khóa bí mật tương ứng. Nói cách khác, mọi người biết khóa công khai đều có thể mã hóa thông tin để gửi nhưng chỉ có người biết khóa riêng (bí mật) mới có thể giải mã được thông tin đó.

Khi sử dụng phương pháp mã hóa bất đối xứng, người gửi tin A sử dụng khóa công khai để mã hóa thông điệp và gửi cho người nhận B. B sử dụng khóa bí mật để giải mã. Nếu có một người C khác phát hiện ra mã thông điệp và thông tin về khóa công khai đã được công bố cũng rất khó có khả năng giải mã do không nắm được khóa bí mật của B.

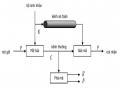
Quá trình truyền tin sử dụng phương pháp mã hóa bất đối xứng có thể mô tả như sau: Người nhận tin B phát sinh ra một cặp khóa: Khóa công khai Kc và khóa bí mật Kr. B gửi khóa công khai Kc cho A (và có thể công bố cho tất cả mọi người) còn khóa bí mật Kr được B giữ một cách an toàn. A dùng khóa Kc để mã hóa thông điệp và gửi bản mã cho B, B dùng khóa bí mật Kr để giải mã. Có thể mô tả quá trình này bằng sơ đồ như Hình 4.6.

Mô hình xác thực sử dụng khóa công khai được minh họa trong Hình 4.7. Giả sử A cần gửi một bản thông báo kèm theo xác thực của mình

cho B. A sẽ mã hóa bản thông báo bằng khóa riêng của A trước khi gửi đi. B nhận được sẽ dùng khóa công khai của A để giải mã ra thông điệp ban đầu. Trong trường hợp này, B có thể tin rằng thông báo này đích thị do A gửi do không ai có thể biết khóa riêng của A để giả mạo.



Bẻ khóa C

Người gửi

A

x

Mã hóa

y

Giải mã

Người nhận

x B

Kc

kr

Khóa mã của B


Hình 4.6. Sơ đồ truyền tin bằng mã hóa khóa công khai


4.3.2. Ưu điểm và nhược điểm của hệ mã hóa không đối xứng

Ưu điểm của hệ thống mã hóa khóa công khai:

(1) Đơn giản trong việc lưu chuyển khóa vì chỉ cần đăng ký một khóa công khai và những người muốn trao đổi sẽ lấy khóa này về để mã hóa thông tin truyền đi, không cần phải có một kênh bí mật để truyền khóa mã,

(2) Mỗi người chỉ cần một cặp khóa công khai - khóa bí mật là có thể trao đổi thông tin với tất cả mọi người trong kênh truyền,

(3) Là tiền đề cho sự ra đời của chữ ký số và các phương pháp chứng thực số sau này.

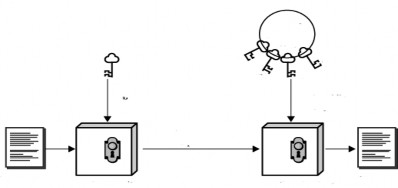
Hình 4 7 Cơ chế xác thực bằng hệ mã hóa khóa công khai Nhưng việc tìm được 1


Hình 4.7. Cơ chế xác thực bằng hệ mã hóa khóa công khai


Nhưng việc tìm được một thuật toán mã hóa thỏa mãn được các yêu cầu đó là không dễ dàng, do một thuật toán mã hóa như vậy cần phải thỏa mãn các yêu cầu sau:

(1) Dễ dàng tạo ra được cặp khóa công khai và bí mật (KU, KR),

(2) Dễ dàng tính được bản mã C = EKU(M),

(3) Có thể dễ dàng giải mã M = DKR(C),

(4) Đối thủ không thể xác định được KR khi biết KU,

(5) Đối thủ không thể xác định được M khi biết KU và C,

(6) Một trong hai khóa có thể dùng mã hóa trong khi khóa kia có thể dùng giải mã: M = DKR(EKU(M)) = DKU(EKR(M)).

Hạn chế của hệ mã hóa khóa công khai là tốc độ xử lý tốn nhiều thời gian và cơ chế xác thực cần nhiều không gian trống.

Về tốc độ xử lý: Các giải thuật trong mã hoá khóa công khai chủ yếu dùng các phép nhân nên tốc độ chậm hơn nhiều so với các giải thuật mã hoá đối xứng, vì vậy, không thích hợp cho những trường hợp mã hóa thông thường và chỉ phù hợp cho các thông tin khi cần trao đổi khóa bí mật đầu phiên truyền tin.

Tính xác thực của khóa công khai: Khi sử dụng phương pháp mã hoá khoá công khai có thể gặp tình huống là khóa công khai có thể bị giả mạo. kẻ tấn công có thể sinh ra một cặp khóa sau đó chuyển cho A khóa công khai và nói đó là khóa công khai của B. Nếu A vô tình sử dụng khóa công khai giả này thì mọi thông tin (mặc dù đã được mã hóa) của A truyền đi đều bị kẻ tấn công đọc được. Tình huống xấu này có thể được giải quyết bởi một bên thứ ba được tin cậy đứng ra chứng nhận khóa công khai, những khóa công khai đã được chứng nhận gọi là chứng thực điện tử. Nó được một tổ chức tin cậy gọi là tổ chức chứng thực khóa công khai Certificate Authority (CA) như VeriSign, Entrust, CyberTrust,... tạo ra. Có thể sử dụng khóa công khai đã được CA chứng nhận để trao đổi thông tin với mức độ bảo mật cao. Như vậy, khi sử dụng mã hoá khoá công khai thì bất cứ ai cũng có thể tạo ra một khóa và công bố đó là của một người khác và chừng nào việc giả mạo chưa bị phát hiện thì đều có thể đọc được nội dung các thông báo gửi cho người kia. Do đó cần có cơ chế đảm bảo những người đăng ký khóa là đáng tin.

4.3.3. Hệ mã hóa RSA

Hệ mã hóa này được Rivest, Shamir và Adleman mô tả lần đầu tiên năm 1977 tại trường Đại học MIT, hệ mã hóa RSA là hệ mã hóa khóa công khai phổ dụng nhất hiện nay và được áp dụng vào hầu hết các ứng dụng thực tế.

RSA sử dụng phương pháp mã hóa khối với mỗi khối là một số nguyên < n. Thông thường kích cỡ của n là 1024 bit ≈ 309 chữ số trong hệ thập phân. Hệ mã hóa này được đăng ký bản quyền năm 1983 và hết hạn vào năm 2000, nghĩa là hiện nay thuật toán có thể sử dụng rộng rãi mà không vi phạm luật sở hữu trí tuệ. Tính an toàn của nó phụ thuộc vào độ khó khăn trong việc phân tích thừa số của một số nguyên lớn. Hệ mã hóa RSA có ba bước để thực hiện:

Bước 1: Xây dựng cặp khóa (Kc, Kr) Bước 2: Mã hóa thông điệp bằng (Kc) Bước 3: Giải mã thông điệp bằng (Kr)

Có thể hình dung hệ mã hóa RSA đơn giản như trường hợp sau:

Giả sử A và B cần trao đổi thông tin bí mật thông qua một kênh truyền thông không an toàn (ví dụ như qua mạng Internet). Để sử dụng hệ mã hóa RSA trong quá trình truyền tin an toàn, đầu tiên B tạo ra cho mình một cặp khóa gồm khóa công khai Kc và khóa bí mật Kr theo các bước như sau:

Bước 1: Thuật toán sinh khóa

1. Chọn 2 số nguyên tố khá lớn (>1024bit) P và Q, P ≠ Q

2. Lấy tích số: N = P*Q, N được gọi là modulo mã hóa.

3. Chọn số e sao cho: 1< e < P*Q, e và tích (P-1)(Q-1) là nguyên tố cùng nhau, e được gọi là số mũ mã hóa hay số e.

4. Tính số d sao cho tích số d*e ≡ 1 mod [(P-1)(Q-1)] có nghĩa là tích số d*e chia cho tích số (P-1)(Q-1) có số dư là 1, hay là (d*e - 1) chia hết cho tích (P-1)(Q-1).

Ta dùng phương pháp thử và loại dần các số nguyên X sao cho có được: d = [X*(P-1)(Q-1) +1]/e là một số nguyên, d được gọi là số mũ giải mã hay số d.

Khi đó khóa công khai B gửi cho A hoặc bất kỳ người nào muốn trao đổi thông tin với BA qua các kênh truyền thông là cặp số (N, e), cặp (N,e) gọi là khóa công khai Kc.

Khóa bí mật B giữ cho riêng mình là cặp số (N, d), cặp (N,d) gọi là khóa bí mật

Bước 2: Mã hóa thông điệp

Khi A nhận được khóa công khai Kc của B gửi, A muốn gửi thông điệp (plaintext) T (thông điệp đã được số hóa, T thực ra là một con số dạng nhị phân được đổi thành số thập phân nào đó) cho B thì A tiến hành các bước mã hóa như sau:

- A mã hóa bằng phép toán: Te mod N = C; T = plaintext, C = ciphertext. Phép toán “lũy thừa theo modulo” có nghĩa là lấy T lũy thừa mũ e rồi chia cho N và lấy số dư.

- A sẽ gửi thông điệp đã mã hóa C cho B.

Bước 3: Giải mã thông điệp

Khi B nhận được bản mã C của A gửi cho mình, B sẽ tiến hành giải mã như sau:

- B giải mã bằng phép toán: Cd mod N = T.

- Như vậy là ở đây, cần phải chứng minh được rằng: (TE mod N)D mod N = T.

Điều này đã được chứng minh bằng cách ứng dụng Định lý Trung Hoa về số dư (The Chinese Remainders Theorem), thực chất việc tìm khóa riêng d chính là tìm một phép toán ngược trong vành modulo N của e.

Ví dụ các bước thực hiện hệ mã hóa RSA như sau:

Bước 1: Sinh cặp khóa

Giả sử B tiến hành xây dựng cặp khóa như sau: Chọn 2 số nguyên tố: p = 17; q = 11

Tính N = p q = 17 11 = 187

Tính (n) = (p - 1) (q - 1) = 16 10 = 160

Chọn e: gcd(e, 160) = 1 và 1 < e < 160; lấy e = 7 Xác định d: de ≡ 1 mod 160 và d ≤ 187

Giá trị d = 23 vì 23 7 = 161 = 1 160 + 1 Công bố khóa công khai Kc = {7, 187}

Giữ bí mật khóa riêng Kr = {23, 187} Hủy bỏ các giá trị bí mật p = 17 và q = 11 Bước 2: Mã hóa thông điệp

Giả sử A muốn gửi cho B một thông điệp T=12

Khi đó, A tiến hành lấy cặp khóa công khai Kc ={7, 187} để mã hóa T như sau:

..... Xem trang tiếp theo?
⇦ Trang trước - Trang tiếp theo ⇨

Ngày đăng: 18/05/2023